Comment vérifier si les données de séries chronologiques sont stationnaires à l'aide de Python ?

Une série chronologique est une série de points de données enregistrés à intervalles réguliers. Il est utilisé pour étudier les tendances des modèles, les relations entre les variables et les changements sur une période de temps définie. Des exemples courants de séries chronologiques incluent les cours des actions, les conditions météorologiques et les indicateurs économiques.

Analysez les données de séries chronologiques grâce à des techniques statistiques et mathématiques. L'objectif principal des séries chronologiques est d'identifier des modèles et des tendances dans les données précédentes afin de prédire les valeurs futures.

Les données sont dites stationnaires, si elles ne changent pas avec le temps. Il est nécessaire de vérifier si les données sont stationnaires ou non. Il existe différentes manières de vérifier si les données des séries chronologiques sont stationnaires, voyons-les une par une. un.

Dickey-Fuller augmenté (ADF)

Augmented Dickey-Fuller (ADF) est un test statistique qui vérifie la présence des racines unitaires disponibles dans les données de la série chronologique. La racine unitaire est la donnée qui est non stationnaire. Elle renvoie la valeur statique et p du test en sortie.

Dans la sortie, si la valeur p est inférieure à 0,05, cela signifie des données de séries chronologiques non stationnaires. Vous trouverez ci-dessous un exemple de données stationnaires ADF. Nous avons une fonction en Python appelée adfuller() qui est disponible dans le package statsmodel pour vérifier si les données de la série chronologique sont stationnaires ou non.

Exemple

Dans cet exemple, nous trouvons la statistique ADF et la valeur p du Dickey Fuller augmenté en utilisant la fonction adfuller() du package statsmodel de python.

from statsmodels.tsa.stattools import adfuller
import pandas as pd
data = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv',parse_dates=['date'], index_col='date')
t_data = data.loc[:, 'value'].values
result = adfuller(t_data)
print("The result of adfuller function:",result)
print('ADF Statistic:', result[0])
print('p-value:', result[1])

Sortie

Voici le résultat produit après l'exécution du programme ci-dessus –

The result of adfuller function: (3.145185689306744, 1.0, 15, 188, {'1%': -3.465620397124192, '5%': -2.8770397560752436, '10%': -2.5750324547306476}, 549.6705685364172)
ADF Statistic: 3.145185689306744
p-value: 1.0

Test KPSS

Un autre test pour vérifier la racine unitaire est le test KPSS. Son abréviation est Kwiatkowski-Phillips-Schmidt-Shin. Nous avons une fonction appelée kpss() dans le package statsmodels pour vérifier les racines unitaires dans les données de séries chronologiques.

Exemple

Vous trouverez ci-dessous un exemple de recherche de racines unitaires dans des données de séries chronologiques.

from statsmodels.tsa.stattools import kpss
import pandas as pd
data = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv',parse_dates=['date'], index_col='date')
t_data = data.loc[:, 'value'].values
from statsmodels.tsa.stattools import kpss
result = kpss(data)
print("The result of kpss function:",result)
print('KPSS Statistic:', result[0])
print('p-value:', result[1])

Sortie

Ce qui suit est le résultat de sortie de la fonction kpss() dans le package statsmodels.

The result of kpss function: (2.0131256386303322, 0.01, 9, {'10%': 0.347, '5%': 0.463, '2.5%': 0.574, '1%': 0.739})
KPSS Statistic: 2.0131256386303322
p-value: 0.01

Statistiques de défilement

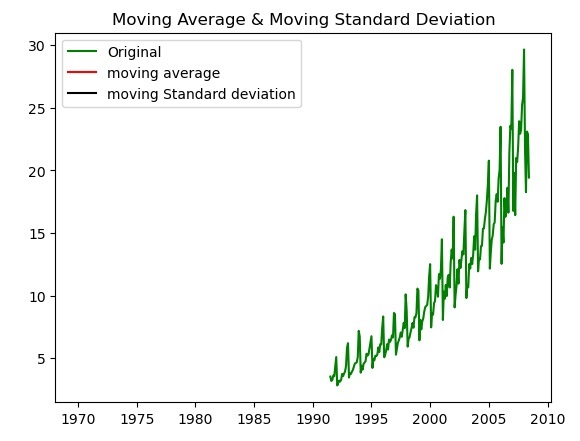
Une autre façon de vérifier les données de séries chronologiques consiste à tracer la moyenne mobile et l'écart type mobile des données de séries chronologiques données et à vérifier si les données restent constantes. Si les données changent au fil du temps dans le graphique, les données de la série chronologique ne sont pas stationnaires.

Exemple

Ce qui suit est un exemple pour vérifier la variation des données en traçant la moyenne mobile et l'écart type mobile à l'aide de la fonction plot() de la bibliothèque matplotlib.

import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv',parse_dates=['date'], index_col='date')
t_data = data.loc[:, 'value'].values
moving_avg = t_data.mean()
moving_std = t_data.std()
plt.plot(data, color='green', label='Original')
plt.plot(moving_avg, color='red', label='moving average')
plt.plot(moving_std, color='black', label='moving Standard deviation')
plt.legend(loc='best')
plt.title('Moving Average & Moving Standard Deviation')
plt.show()

Sortie

Vous trouverez ci-dessous le résultat de la normalisation des données de séries chronologiques en traçant la moyenne mobile et l'écart type mobile.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!