développement back-end
C++
Quelle est l'aire du carré formé en joignant à plusieurs reprises les milieux ?
Quelle est l'aire du carré formé en joignant à plusieurs reprises les milieux ?
L'aire d'un carré est égale au produit des longueurs des côtés du carré.
Nous considérons une figure dans laquelle le milieu des côtés de chaque carré forme un autre carré. Et ainsi de suite jusqu'à un nombre précis de carrés.
Ce graphique montre un carré formé en reliant les milieux des carrés.
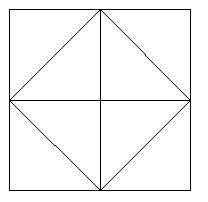
Pour cette figure, laissez la longueur du côté être a,
La longueur du côté du carré intérieur sera
L2 = (a/2)<sup>2</sup> + (a/2)<sup>2</sup>
L2 = a<sup>2</sup>(1/4 + 1/4) = a<sup>2</sup>(1/2) = a<sup>2</sup>/2
L = a<sup>2</sup>/ (\sqrt{2}).L'aire du carré 2 = L2 = a2/2.
Pour le carré suivant, carré 3 Aire de = a2/4
Prenons un exemple, tge
Maintenant, nous pouvons déduire l'aire des carrés continus à partir d'ici,
a2, a 2/2, a2 /4, a2/8, …..
Il s'agit d'une suite géométrique avec une raison commune de ½, où a2 est le premier terme.
Exemple
#include <stdio.h>
#include <math.h>
int main() {
double L = 2, n = 10;
double firstTerm = L * L;
double ratio = 1 / 2.0;
double are = firstTerm * (pow(ratio, 10)) ;
printf("The area of %lfth square is %lf", n , sum);
return 0;
}Sortie
The area of 10th square is 0.003906
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Outils d'IA chauds
Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes
AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.
Undress AI Tool
Images de déshabillage gratuites
Clothoff.io
Dissolvant de vêtements AI
AI Hentai Generator
Générez AI Hentai gratuitement.
Article chaud
Outils chauds
Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit
SublimeText3 version chinoise
Version chinoise, très simple à utiliser
Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP
Dreamweaver CS6
Outils de développement Web visuel
SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
Analyse de la signification et de l'utilisation du point médian en PHP
Mar 27, 2024 pm 08:57 PM
[Analyse de la signification et de l'utilisation du point médian PHP] En PHP, le point médian (.) est un opérateur couramment utilisé, utilisé pour connecter deux chaînes ou propriétés ou méthodes d'objets. Dans cet article, nous approfondirons la signification et l’utilisation des points médians en PHP, en les illustrant avec des exemples de code concrets. 1. Opérateur de point médian de chaîne de connexion L’utilisation la plus courante en PHP consiste à connecter deux chaînes. En plaçant . entre deux chaînes, vous pouvez les assembler pour former une nouvelle chaîne. $string1=&qu
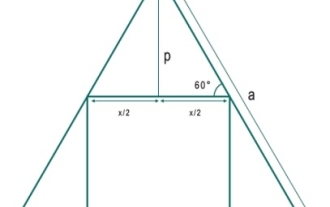
Quel est le plus grand carré pouvant être inscrit dans un triangle équilatéral ?
Sep 22, 2023 pm 06:21 PM
Nous verrons ici l'aire du plus grand carré pouvant être inscrit dans un triangle équilatéral. La longueur du côté du triangle est « a » et la longueur du côté du carré est x. La longueur du côté 'a' du triangle est − donc x est − Exemple #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
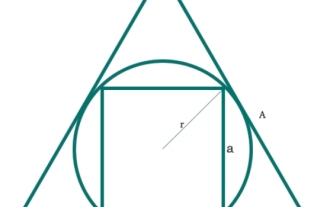
Dans un programme C, traduisez en chinois : Quelle est l'aire d'un carré inscrit dans un cercle inscrit dans un triangle équilatéral ?
Aug 31, 2023 pm 12:25 PM
Nous verrons ici que l'aire d'un carré est inscrite dans un cercle, et que le cercle est inscrit dans un triangle équilatéral. Le côté du carré est "a". Le rayon du cercle est "r" et le côté de l'hexagone est "A". Le graphique est présenté ci-dessous. Donc la diagonale du carré est - donc l'aire du carré est - Exemple #include<iostream>#include<cmath>usingnamespacestd;floatarea(floatA){//Aisthesideofthetriangle if(A<0)//ifthevalueisne
Trouver l'aire d'un cercle inscrit dans un carré en Java
Aug 19, 2023 pm 04:53 PM
Un cercle est autour d'un diagramme bidimensionnel en forme qui n'a pas de coins. Chaque cercle a un point d'origine et chaque point du cercle maintient une distance égale par rapport à l'origine. La distance entre l'origine et le point dans un cercle est connue sous le nom de rayon du cercle. Et de même, si nous traçons une ligne à partir de
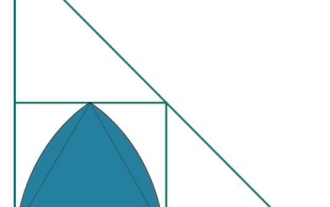
Quel est le plus grand triangle de Ruero inscrit dans un carré qui est un triangle rectangle ?
Sep 04, 2023 pm 10:29 PM
Ici, nous verrons l'aire du plus grand triangle de Reuleaux inscrite dans un carré, qui à son tour est inscrit dans un triangle rectangle. La longueur du côté du carré est « a ». La hauteur d'un triangle de Reuleaux est x. La base du triangle est b, la hauteur est l et l'hypoténuse est h. Nous savons qu'un carré inscrit dans un triangle rectangle de hauteur l et de base b a une longueur de côté - la hauteur d'un triangle de Reuleaux est la même que a. Donc a=x. Par conséquent, l'aire d'un triangle de Reuleaux est - Exemple#include<iostream>#include<cmath>usingnamespacestd;fl
En C, le plus grand triangle de Reuleaux à l'intérieur d'un carré
Sep 07, 2023 pm 12:29 PM
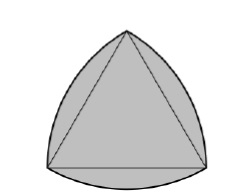
Un triangle de Lule est une forme formée par l'intersection de trois disques, le centre de chaque disque étant à la limite des deux autres disques. Sa limite est une courbe de largeur constante et, mis à part le cercle lui-même, c'est la courbe de ce type la plus simple et la plus connue. Une largeur constante signifie que l'espacement entre chacune des deux lignes de support parallèles est le même, quelle que soit leur orientation. Parce que tous ses diamètres sont les mêmes. Les limites d'un triangle de Lule sont des courbes de largeur constante basées sur des triangles équilatéraux. Tous les points d'une arête sont équidistants du sommet opposé. La formule pour construire un triangle de Lule Si la courbe est basée sur un triangle équilatéral et que la longueur du côté du triangle est h, alors l'aire du triangle de Lule est A=(π*h2)/2–2*( Zoneo
Programme C pour calculer l'aire d'un carré dans un cercle inscrit dans un hexagone
Aug 28, 2023 pm 08:41 PM
Étant donné un carré inscrit dans un cercle inscrit par un hexagone régulier, nous devons trouver l'aire du carré, et pour ce faire, nous devons trouver la relation entre les longueurs des côtés du carré et les longueurs des côtés de l'hexagone régulier . La formule mathématique du rayon du cercle inscrit d'un hexagone régulier est : r=A√3/2 Puisque la diagonale du carré est égale au diamètre du cercle, la relation entre le rayon et la longueur du côté est : a=√r Selon l'hexagone régulier Longueur du côté de, a=√3A/√2, Donc l'aire du carré, Area=a2=(√3A/√2)2 Exemple #include<stdio. h>#inclu
Quelle est l'aire d'une feuille dans un carré ?
Aug 26, 2023 pm 05:13 PM
Ici, nous verrons comment calculer l'aire d'un objet en forme de feuille qui se trouve dans un carré ABCD. Chaque côté du carré a une longueur « a ». La feuille comporte deux parties égales. L'aire de chaque partie est p, maintenant − l'aire de la feuille entière est 2p. Exemple #include<iostream>usingnamespacestd;floatleafArea(floata){ return(a*a*(3.1415/2-1));}intmain(){ floatsquare
