Quelles sont les méthodes de tri ?
Les méthodes de tri incluent le tri à bulles, le tri par sélection, le tri par insertion, le tri rapide, le tri par fusion, le tri par tas, le tri par comptage et le tri par seau. Introduction détaillée : 1. Le tri à bulles est un algorithme de tri simple. Il parcourt à plusieurs reprises le tableau à trier, compare deux éléments à la fois et les échange si l'ordre est erroné. Le travail de parcours du tableau est répété jusqu'à ce qu'il n'y en ait plus. plus d'éléments. Si un échange est à nouveau nécessaire, cela signifie que la séquence a été triée ; 2. Le tri par sélection est un algorithme de tri simple et intuitif. Son principe de fonctionnement est de sélectionner à chaque fois le plus petit élément parmi les éléments de données à trier, et ainsi de suite.

La méthode de tri est l'un des algorithmes de base que nous devons souvent utiliser en programmation. Voici quelques méthodes de tri courantes et leurs descriptions :
Tri à bulles
Le tri à bulles est un algorithme de tri simple qui parcourt à plusieurs reprises la séquence à trier, en comparant deux éléments à la fois, en les échangeant s'ils sont incorrects. commande. Le travail de parcours du tableau est répété jusqu'à ce qu'aucun échange ne soit plus nécessaire, ce qui signifie que le tableau a été trié.
Complexité temporelle : O(n^2)
Tri par sélection
Le tri par sélection est un algorithme de tri simple et intuitif. Son principe de fonctionnement est de sélectionner à chaque fois le plus petit (ou le plus grand) élément parmi les éléments de données à trier et de le stocker au début de la séquence jusqu'à ce que tous les éléments de données à trier soient disposés.
Complexité temporelle : O(n^2)
Tri par insertion
Le tri par insertion est un algorithme de tri simple et intuitif. Il fonctionne en construisant une séquence ordonnée pour les données non triées, il parcourt la séquence triée d'avant en arrière, trouve la position correspondante et l'insère.
Complexité temporelle : O(n^2)
Tri rapide
Le tri rapide utilise le principe de diviser pour régner, sélectionnez d'abord un élément d'axe, puis divisez tous les éléments en deux parties, une partie Les éléments sont tous plus petit que l'élément pivot, et les éléments de l'autre partie sont tous plus grands que l'élément pivot. Triez ensuite rapidement les deux parties séparément. Une fois la récursion terminée, la séquence entière devient ordonnée.
Complexité temporelle : la complexité temporelle moyenne est O(n log n) et le pire des cas est O(n^2).
Merge Sort
Merge Sort est également un algorithme de tri qui utilise le principe diviser pour régner. Il divise un tableau en deux sous-tableaux, fusionne et trie les deux sous-tableaux séparément, puis fusionne les résultats dans un tableau ordonné.
Complexité temporelle : la complexité temporelle moyenne est O(n log n) et le pire des cas est O(n^2).
Tri par tas
Le tri par tas est un tri par sélection arborescente, qui constitue une amélioration efficace du tri par sélection directe. Son idée de base est de construire la séquence à trier dans un grand tas supérieur. À ce stade, la valeur maximale de la séquence entière est le nœud racine en haut du tas. Échangez-le ensuite avec le dernier élément, qui est la valeur maximale. Reconstruisez ensuite les n-1 éléments restants en un tas, de sorte que la plus petite valeur suivante de n éléments soit obtenue. Si vous exécutez ceci à plusieurs reprises, vous pouvez obtenir une séquence ordonnée.
Complexité temporelle : O(n log n)
Counting Sort
Counting Sort n'est pas un algorithme de tri basé sur une comparaison, et sa complexité est O(n). Il s'agit d'un algorithme de tri linéaire à complexité temporelle adapté au tri d'entiers dans une certaine plage. Il fonctionne en calculant le nombre d'occurrences de chaque élément de la séquence à trier, puis en plaçant les éléments dans la position correspondante en fonction du nombre d'occurrences.
Complexité temporelle : O(n+k), où k est la plage d'éléments à trier.
Bucket Sort
Bucket Sort est un algorithme de tri avec une complexité temporelle linéaire, adapté au tri des nombres à virgule flottante dans une certaine plage. Son principe de fonctionnement est de diviser les éléments à trier en plusieurs compartiments, puis d'utiliser des algorithmes tels que le tri rapide à l'intérieur de chaque compartiment pour trier. Enfin, les éléments de chaque compartiment sont fusionnés dans une séquence ordonnée dans l'ordre.
Complexité temporelle : la complexité temporelle moyenne est O(n), et dans le pire des cas, elle est O(n^2).
Ce sont des méthodes de tri courantes, chaque méthode a ses scénarios applicables, ses avantages et ses inconvénients. Dans la programmation réelle, il est nécessaire de sélectionner un algorithme de tri approprié basé sur des problèmes et des données spécifiques.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1359
1359
 52
52
 Comment trier les photos par date prise sous Windows 11/10
Feb 19, 2024 pm 08:45 PM
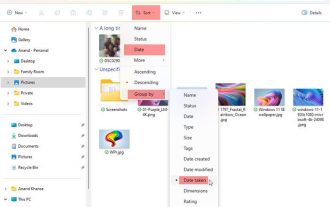
Comment trier les photos par date prise sous Windows 11/10
Feb 19, 2024 pm 08:45 PM
Cet article explique comment trier les images en fonction de la date de prise de vue dans Windows 11/10 et explique également ce qu'il faut faire si Windows ne trie pas les images par date. Dans les systèmes Windows, organiser correctement les photos est crucial pour faciliter la recherche des fichiers image. Les utilisateurs peuvent gérer des dossiers contenant des photos en fonction de différentes méthodes de tri telles que la date, la taille et le nom. De plus, vous pouvez définir l'ordre croissant ou décroissant selon vos besoins pour organiser les fichiers de manière plus flexible. Comment trier les photos par date de prise sous Windows 11/10 Pour trier les photos par date de prise sous Windows, procédez comme suit : Ouvrez Images, Bureau ou tout dossier dans lequel vous placez des photos. Dans le menu du ruban, cliquez sur
 Comment trier les e-mails par expéditeur, sujet, date, catégorie, taille dans Outlook
Feb 19, 2024 am 10:48 AM
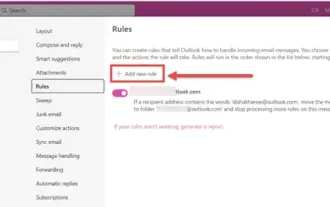
Comment trier les e-mails par expéditeur, sujet, date, catégorie, taille dans Outlook
Feb 19, 2024 am 10:48 AM
Outlook propose de nombreux paramètres et fonctionnalités pour vous aider à gérer votre travail plus efficacement. L’une d’elles est l’option de tri qui vous permet de classer vos emails en fonction de vos besoins. Dans ce didacticiel, nous allons apprendre à utiliser la fonction de tri d'Outlook pour organiser les e-mails en fonction de critères tels que l'expéditeur, l'objet, la date, la catégorie ou la taille. Cela vous permettra de traiter et de trouver plus facilement des informations importantes, ce qui vous rendra plus productif. Microsoft Outlook est une application puissante qui facilite la gestion centralisée de vos plannings de messagerie et de calendrier. Vous pouvez facilement envoyer, recevoir et organiser des e-mails, tandis que la fonctionnalité de calendrier intégrée facilite le suivi de vos événements et rendez-vous à venir. Comment être dans Outloo
 Filtrage et tri des données XML à l'aide de Python
Aug 07, 2023 pm 04:17 PM
Filtrage et tri des données XML à l'aide de Python
Aug 07, 2023 pm 04:17 PM
Implémentation du filtrage et du tri des données XML à l'aide de Python Introduction : XML est un format d'échange de données couramment utilisé qui stocke les données sous forme de balises et d'attributs. Lors du traitement de données XML, nous devons souvent filtrer et trier les données. Python fournit de nombreux outils et bibliothèques utiles pour traiter les données XML. Cet article explique comment utiliser Python pour filtrer et trier les données XML. Lecture du fichier XML Avant de commencer, nous devons lire le fichier XML. Python possède de nombreuses bibliothèques de traitement XML,
 Développement PHP : Comment implémenter les fonctions de tri et de pagination des données des tables
Sep 20, 2023 am 11:28 AM
Développement PHP : Comment implémenter les fonctions de tri et de pagination des données des tables
Sep 20, 2023 am 11:28 AM
Développement PHP : comment implémenter des fonctions de tri et de pagination des données de table Dans le développement Web, le traitement de grandes quantités de données est une tâche courante. Pour les tableaux devant afficher une grande quantité de données, il est généralement nécessaire de mettre en œuvre des fonctions de tri et de pagination des données pour offrir une bonne expérience utilisateur et optimiser les performances du système. Cet article explique comment utiliser PHP pour implémenter les fonctions de tri et de pagination des données de table et donne des exemples de code spécifiques. La fonction de tri implémente la fonction de tri dans le tableau, permettant aux utilisateurs de trier par ordre croissant ou décroissant selon différents champs. Ce qui suit est un formulaire de mise en œuvre
 Programme C++ : réorganiser la position des mots par ordre alphabétique
Sep 01, 2023 pm 11:37 PM
Programme C++ : réorganiser la position des mots par ordre alphabétique
Sep 01, 2023 pm 11:37 PM
Dans ce problème, une chaîne est donnée en entrée et nous devons trier les mots apparaissant dans la chaîne par ordre lexicographique. Pour ce faire, nous attribuons un index commençant à 1 à chaque mot de la chaîne (séparés par des espaces) et obtenons le résultat sous forme d'index triés. String={"Hello","World"}"Hello"=1 "World"=2 Puisque les mots dans la chaîne d'entrée sont dans l'ordre lexicographique, la sortie imprimera "12". Examinons quelques scénarios d'entrée/résultat - en supposant que tous les mots de la chaîne d'entrée sont identiques, regardons les résultats - Entrée :{"hello","hello","hello"}Résultat : 3 Résultat obtenu
 Comment la méthode Arrays.sort() en Java trie-t-elle les tableaux par comparateur personnalisé ?
Nov 18, 2023 am 11:36 AM
Comment la méthode Arrays.sort() en Java trie-t-elle les tableaux par comparateur personnalisé ?
Nov 18, 2023 am 11:36 AM
Comment la méthode Arrays.sort() en Java trie-t-elle les tableaux par comparateur personnalisé ? En Java, la méthode Arrays.sort() est une méthode très utile pour trier les tableaux. Par défaut, cette méthode trie par ordre croissant. Mais parfois, nous devons trier le tableau selon nos propres règles définies. À ce stade, vous devez utiliser un comparateur personnalisé (Comparator). Un comparateur personnalisé est une classe qui implémente l'interface Comparator.
 Comment trier les scores WPS
Mar 20, 2024 am 11:28 AM
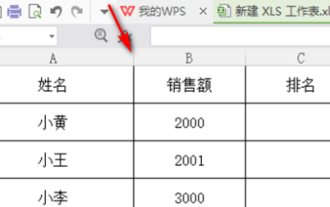
Comment trier les scores WPS
Mar 20, 2024 am 11:28 AM
Dans notre travail, nous utilisons souvent le logiciel wps. Il existe de nombreuses façons de traiter les données dans le logiciel wps, et les fonctions sont également très puissantes. Nous utilisons souvent des fonctions pour trouver des moyennes, des résumés, etc. des méthodes qui peuvent être utilisées pour les données statistiques ont été préparées pour tout le monde dans la bibliothèque du logiciel WPS. Ci-dessous, nous présenterons les étapes à suivre pour trier les scores dans WPS. Après avoir lu ceci, vous pourrez tirer les leçons de cette expérience. 1. Ouvrez d’abord le tableau qui doit être classé. Comme indiqué ci-dessous. 2. Entrez ensuite la formule =rank(B2, B2 : B5, 0) et assurez-vous de saisir 0. Comme indiqué ci-dessous. 3. Après avoir saisi la formule, appuyez sur la touche F4 du clavier de l'ordinateur. Cette étape consiste à changer la référence relative en référence absolue.
 Comment trier les tableaux WPS pour faciliter les statistiques de données
Mar 20, 2024 pm 04:31 PM
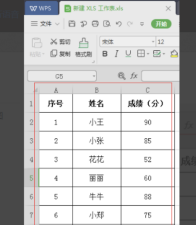
Comment trier les tableaux WPS pour faciliter les statistiques de données
Mar 20, 2024 pm 04:31 PM
WPS est un logiciel bureautique très complet, comprenant l'édition de texte, les tableaux de données, les présentations PPT, les formats PDF, les organigrammes et d'autres fonctions. Parmi eux, ceux que nous utilisons le plus sont les textes, les tableaux et les démonstrations, et ce sont aussi ceux que nous connaissons le mieux. Dans notre travail d'étude, nous utilisons parfois des tableaux WPS pour établir des statistiques de données. Par exemple, l'école comptera les scores de chaque élève. Si nous devons trier manuellement les scores de tant d'élèves, ce sera vraiment un casse-tête. en fait, nous n'avons pas à nous inquiéter, car notre table WPS a une fonction de tri pour résoudre ce problème pour nous. Apprenons ensuite comment trier les WPS ensemble. Étapes de la méthode : Étape 1 : Nous devons d’abord ouvrir la table WPS qui doit être triée



