 développement back-end
développement back-end
 C++
C++
 Si pas plus de deux points du plan sont colinéaires, quel est le nombre de triangles ?
Si pas plus de deux points du plan sont colinéaires, quel est le nombre de triangles ?
Si pas plus de deux points du plan sont colinéaires, quel est le nombre de triangles ?
Voyons comment compter le nombre de triangles sur un plan étant donné n points et limiter le nombre de points colinéaires à deux maximum.
Le calcul du nombre de triangles dans un plan ne comportant pas plus de deux points colinéaires est un problème typique de la géométrie computationnelle, qui est appliqué à l'infographie, au traitement d'images et à d'autres domaines de l'informatique.
Par exemple, lors de la création d'une image 2D à partir d'une scène 3D dans des graphiques 3D, le problème peut survenir du calcul de triangles dans un plan ne comportant pas plus de deux points colinéaires. Dans ce cas, le processus de comptage de triangles peut être utilisé pour déterminer combien de triangles sont présents dans l’image 2D finale après projection de la scène 3D sur un plan. Cela vous permet de déterminer la complexité de la scène et d'augmenter la vitesse de rendu.
En traitement d'image, nous pouvons vouloir compter le nombre d'objets ou de formes uniques dans une image, cette question est utile. Dans ce cas, nous pouvons représenter l’image comme une collection de points sur un plan, puis compter le nombre de triangles qui peuvent être créés entre ces points en appliquant des techniques de comptage de triangles. Nous pouvons déterminer le nombre approximatif d’éléments ou de formes différents dans une image en comptant le nombre de triangles formés.
Instructions
Comprenons ce problème à travers quelques exemples et essayons de le résoudre.
Le but est de déterminer combien de triangles sont formés sur un plan avec n points tels que pas plus de deux points soient colinéaires.
Exemple -
Supposons que N soit le nombre de points sur l'avion.
N = 3
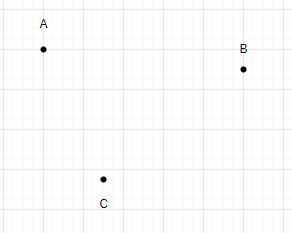
En utilisant ces points, nous ne pouvons dessiner qu'un triangle.
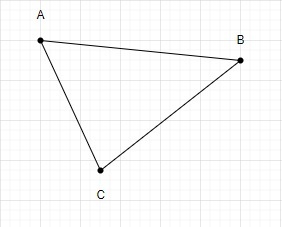
Le nombre total de triangles formés à partir de 3 points est donc 1.
Soit N = 4
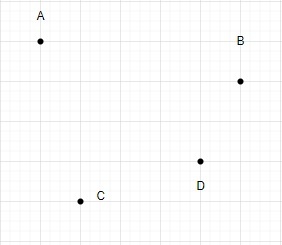
Traçons un triangle en utilisant ces quatre points.
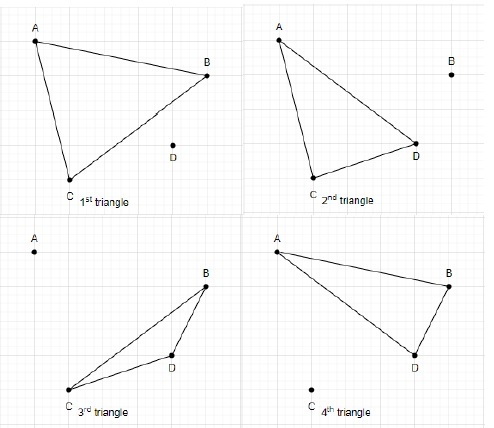
Le nombre total de triangles formés à l'aide de 4 points est de 4.
Regardons quelques-uns des calculs impliqués dans le calcul du nombre de triangles. Ceci peut être obtenu en utilisant des permutations et des combinaisons. Pour construire un triangle, vous avez besoin de 3 points sur le total à la fois.
Ainsi, si un plan contient n points et que pas plus de deux d'entre eux sont colinéaires, alors le nombre de triangles dans le plan est donné par la formule suivante.
$$mathrm{n_{C_{3}}:=:frac{n(n-1):(n-2)}{6}}$$
Méthode
Le programme trouve le nombre de triangles dans le plan si pas plus de deux points sont colinéaires, en utilisant l'algorithme suivant.
Prenez le nombre de points sur le plan en entrée et limitez-le à pas plus de deux points colinéaires.
Calculez le nombre total de triangles en utilisant la formule ci-dessus.
Imprimez le nombre total de triangles en sortie.
Exemple
Programme C++ pour calculer le nombre de triangles dans un plan si pas plus de deux points sont colinéaires.
#include <iostream>
using namespace std;
int main() {
int number_of_points = 4;
int number_of_triangle;
number_of_triangle = number_of_points * (number_of_points - 1) * (number_of_points - 2) / 6;
cout << "Total number of triangles formed using " << number_of_points<< " points = " << number_of_triangle << endl;
return 0;
}
Sortie
Total number of triangles formed using 4 points = 4
Complexité
Complexité temporelle : O(1) puisque ce code effectue un nombre fixe de calculs quelle que soit la taille d'entrée.
Complexité spatiale : O(1) car le code utilise un nombre fixe de variables pour stocker les valeurs d'entrée et les résultats quelle que soit la taille de l'entrée.
Conclusion
Dans cet article, nous essayons d'expliquer la méthode pour trouver le nombre total de triangles possibles avec n points donnés, avec la contrainte qu'il n'y a pas deux points colinéaires. J'espère que cet article vous aidera à mieux apprendre ce concept.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Programme Java pour calculer l'aire d'un triangle à l'aide de déterminants
Aug 31, 2023 am 10:17 AM
Programme Java pour calculer l'aire d'un triangle à l'aide de déterminants
Aug 31, 2023 am 10:17 AM
Introduction Le programme Java pour calculer l'aire d'un triangle à l'aide d'un déterminant est un programme concis et efficace qui peut calculer l'aire d'un triangle à partir des coordonnées de trois sommets. Ce programme est utile à toute personne qui apprend ou travaille avec la géométrie, car il montre comment utiliser les calculs arithmétiques et algébriques de base en Java, ainsi que comment utiliser la classe Scanner pour lire les entrées de l'utilisateur. Le programme demande à l'utilisateur les coordonnées de trois points du triangle, qui sont ensuite lues et utilisées pour calculer le déterminant de la matrice de coordonnées. Utilisez la valeur absolue du déterminant pour vous assurer que l'aire est toujours positive, puis utilisez une formule pour calculer l'aire du triangle et l'afficher à l'utilisateur. Le programme peut être facilement modifié pour accepter des entrées dans différents formats ou pour effectuer des calculs supplémentaires, ce qui en fait un outil polyvalent pour les calculs géométriques. rangs de déterminants
 Écrit en C++, trouvez le nombre de triangles formés par un ensemble de points sur trois droites
Sep 09, 2023 am 09:53 AM
Écrit en C++, trouvez le nombre de triangles formés par un ensemble de points sur trois droites
Sep 09, 2023 am 09:53 AM
Maintenant, nous obtenons plusieurs points présents sur 3 lignes ; par exemple, nous devons savoir combien de triangles ces points peuvent former Input:m=3,n=4,k=5Output:205Input:m=2,n=2, k =1Sortie : 10 Nous appliquerons des mathématiques combinatoires pour résoudre ce problème et formulerons des formules pour résoudre ce problème. Méthode pour trouver une solution Dans cette méthode, nous élaborerons une formule : en appliquant la combinatoire à la situation actuelle, cette formule nous fournira le résultat. Code C++ pour la méthode ci-dessus Il s'agit d'une syntaxe C++ que nous pouvons utiliser comme entrée pour résoudre le problème donné - exemple #include<bits/stdc++.h>#define
 Comment taper le point '丶' à l'aide du clavier ?
Feb 15, 2024 pm 01:51 PM
Comment taper le point '丶' à l'aide du clavier ?
Feb 15, 2024 pm 01:51 PM
Lorsqu'ils tapent sur un clavier, de nombreux utilisateurs sont curieux de savoir comment taper le point « 丶 » sur le clavier ? Jetons donc un œil à la méthode que l'éditeur vous propose pour taper ce symbole « 丶 » sur le clavier. 1. Cliquez sur "丶" et tapez directement sur le clavier [dian]. Vous verrez le signe de ponctuation [丶] sur la barre de sélection. 2. Symboles spéciaux Dans la méthode de saisie Sogou Pinyin, lors du passage en mode chinois, appuyer sur la touche v fera apparaître des symboles spéciaux. Ces symboles incluent des nombres (par exemple : v123), des dates (par exemple : v2013/1/1), des calculs (par exemple : v1+1) et des fonctions (par exemple : v2~3). Ces symboles facilitent la saisie de diverses informations. 2. Appuyez ensuite à nouveau sur la touche numérique, n'importe quel nombre de 0 à 9 peut être utilisé
 Comment vérifier si trois points sont colinéaires en Java ?
Sep 05, 2023 pm 06:41 PM
Comment vérifier si trois points sont colinéaires en Java ?
Sep 05, 2023 pm 06:41 PM
Si trois points sont alignés, on dit qu’ils sont colinéaires. Si les points ne sont pas sur la même droite, ils ne sont pas colinéaires. Cela signifie que si trois points (x1,y1), (x2,y2), (x3,y3) sont sur la même droite, ils sont colinéaires. Parmi eux, x1, y1, x2, y2, x3, y3 sont des points sur l'axe des x et l'axe des y, (x1, y1), (x2, y2), (x3, y3) sont les coordonnées. Mathématiquement, il existe deux façons de déterminer si trois points sont colinéaires. Trouvez l'aire d'un triangle en utilisant les points. Si l'aire du triangle est nulle, alors les trois points sont colinéaires. Formule pour trouver une zone de triangle = 0,5*[x1*(y2-y3)+x2*
 Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Aug 29, 2023 pm 10:25 PM
Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Aug 29, 2023 pm 10:25 PM
Dans cet article, nous sommes confrontés à un problème dans lequel nous devons trouver le nombre total de chemins du point A au point B, où A et B sont des points fixes, c'est-à-dire A est le point du coin supérieur gauche de la grille et B est le point inférieur. point du coin droit, par exemple −Input:N=5Output:252Input:N=4Output:70Input:N=3Output:20 Dans le problème donné, nous pouvons formaliser la réponse et dériver le résultat à travers des observations simples. Méthode de recherche de solution Dans cette méthode, nous dérivons une formule en observant que lorsque nous traversons la grille de A à B, nous devons aller à droite n fois et descendre n fois, ce qui signifie que nous devons trouver toutes les combinaisons de chemins possibles, nous obtenons donc
 Comment trouver la hauteur minimale d'un triangle en fonction de sa base et de son aire en Java ?
Aug 26, 2023 pm 10:25 PM
Comment trouver la hauteur minimale d'un triangle en fonction de sa base et de son aire en Java ?
Aug 26, 2023 pm 10:25 PM
Nous avons l'aire 'a' et la base 'b' du triangle. Conformément à l'énoncé du problème, nous devons trouver la hauteur minimale « h » à l'aide du langage de programmation Java. Comme nous le savons, lorsque la base et la hauteur sont données, l'aire d'un triangle est −$$\mathrm{area\:=\:\frac{1}{2}\:*\:base\:*\ : Height}$$ En utilisant la formule ci-dessus, nous pouvons obtenir la hauteur à partir de -height=(2*area)/base puis en utilisant la méthode intégrée ceil(), nous pouvons obtenir la hauteur minimale. Montrez quelques exemples pour vous montrer la traduction chinoise de l'instance-1 : Exemple-1 Supposons que l'aire donnée = 12 et la base = 6, puis utilisez la formule
 Programme C++ pour imprimer une table de multiplication sous forme de triangle
Sep 15, 2023 pm 01:21 PM
Programme C++ pour imprimer une table de multiplication sous forme de triangle
Sep 15, 2023 pm 01:21 PM
Pour mémoriser certains résultats de multiplication de base sous forme tabulaire ou graphique, utilisez la table de multiplication. Cet article explique comment utiliser C++ pour générer une table de multiplication qui ressemble à un triangle rectangle. La notation triangulaire est efficace dans les rares cas où un grand nombre de résultats peuvent être facilement mémorisés. Dans ce format, le tableau est affiché ligne par ligne et colonne par colonne, chaque ligne contenant uniquement les entrées qui remplissent cette colonne. Pour résoudre ce problème, nous avons besoin d’instructions de boucle de base en C++. Pour afficher les nombres de manière triangulaire, nous avons besoin de boucles imbriquées pour imprimer chaque ligne une par une. Nous verrons comment résoudre ce problème. Voyons l'algorithme et la mise en œuvre pour une meilleure compréhension. L'algorithme prend le nombre de lignes de la table de multiplication souhaitée, disons n. Pour i de 1 à n, procédez comme suit. Pour j allant de 1 à i,
 Nombre maximum de droites distinctes passant par un point de C
Aug 26, 2023 am 10:25 AM
Nombre maximum de droites distinctes passant par un point de C
Aug 26, 2023 am 10:25 AM
On obtient le nombre N pour chaque droite et les coordonnées des deux points (x1,y1) et (x2,y2). Le but est de trouver le nombre maximum de lignes droites à partir des lignes droites données qui peuvent passer par un seul point de telle sorte qu'aucune ligne droite ne se recouvre et qu'aucune rotation ne soit effectuée. Nous représenterons la ligne droite comme (paire)m,c) où y=mx+c et m est la pente m=y2-y1/x2-x1 Étant donné c1!=c2, les lignes avec le même m sont parallèles. Nous calculerons différentes pentes en mètres. Pour une droite verticale, si x1=x2, alors pente=INT_MAX, sinon m. Comprenons avec un exemple. Entrée Ligne1(x1,y1)=(4,10)(x2,y2)=(2,2)Ligne2(x1,y1)=(2





