 développement back-end
développement back-end
 C++
C++
 Solution optimisée en termes d'espace pour le programme LCS en C ?
Solution optimisée en termes d'espace pour le programme LCS en C ?
Solution optimisée en termes d'espace pour le programme LCS en C ?

Ici, nous verrons une méthode d'optimisation spatiale pour le problème LCS. LCS est la sous-séquence commune la plus longue. Si les deux chaînes sont « BHHUBC » et « HYUYBZC », alors la longueur de la sous-séquence est de 4. La méthode de programmation dynamique en fait déjà partie, mais son utilisation prendra plus de place. Nous avons besoin d'un tableau d'ordre m x n, où m est le nombre de caractères dans la première chaîne et n est le nombre de caractères dans la deuxième chaîne.
Ici, nous verrons comment utiliser l'espace auxiliaire O(n). Si nous regardons l’ancienne approche, nous pouvons voir qu’à chaque itération, nous avons besoin des données de la ligne précédente. Toutes les données ne sont pas obligatoires. Donc si on fait un tableau de taille 2n, ce n'est pas un problème. Regardons l'algorithme pour comprendre cette idée.
Algorithme
lcs_problem(X, Y) -
begin
m := length of X
n := length of Y
define table of size L[2, n+1]
index is to point 0th or 1st row of the table L.
for i in range 1 to m, do
index := index AND 1
for j in range 0 to n, do
if i = 0 or j = 0, then
L[index, j] := 0
else if X[i - 1] = Y[j - 1], then
L[index, j] := L[1 – index, j - 1] + 1
else
L[index, j] := max of L[1 – index, j] and L[index, j-1]
end if
done
done
return L[index, n]
endExemple
#include <iostream>
using namespace std;
int lcsOptimized(string &X, string &Y) {
int m = X.length(), n = Y.length();
int L[2][n + 1];
bool index;
for (int i = 0; i <= m; i++) {
index = i & 1;
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0)
L[index][j] = 0;
else if (X[i-1] == Y[j-1])
L[index][j] = L[1 - index][j - 1] + 1;
else
L[index][j] = max(L[1 - index][j], L[index][j - 1]);
}
}
return L[index][n];
}
int main() {
string X = "BHHUBC";
string Y = "HYUYBZC";
cout << "Length of LCS is :" << lcsOptimized(X, Y);
}Sortie
Length of LCS is :4
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1657
1657
 14
14
 1415
1415
 52
52
 1309
1309
 25
25
 1257
1257
 29
29
 1230
1230
 24
24
 Traduisez ce qui suit en chinois : Programme C pour convertir des chiffres romains en nombres décimaux
Sep 05, 2023 pm 09:53 PM
Traduisez ce qui suit en chinois : Programme C pour convertir des chiffres romains en nombres décimaux
Sep 05, 2023 pm 09:53 PM
Vous trouverez ci-dessous un algorithme en langage C pour convertir les chiffres romains en nombres décimaux : Algorithme Étape 1 - Démarrer Étape 2 - Lire les chiffres romains au moment de l'exécution Étape 3 - Longueur : = strlen (roman) Étape 4 - Pour i = 0 à Longueur-1 Étape 4.1-switch(roman[i]) Étape 4.1.1-case'm' : &nbs
 Programme C++ pour comparer l'ordre lexicographique de deux chaînes
Sep 04, 2023 pm 05:13 PM
Programme C++ pour comparer l'ordre lexicographique de deux chaînes
Sep 04, 2023 pm 05:13 PM
La comparaison de chaînes lexicographiques signifie que les chaînes sont comparées dans l’ordre du dictionnaire. Par exemple, s'il y a deux chaînes « pomme » et « appel », la première chaîne viendra en dernier car les trois premiers caractères de « application » sont identiques. Ensuite, pour la première chaîne, le caractère est « l » et dans la deuxième chaîne, le quatrième caractère est « e ». Puisque « e » est plus court que « l », il viendra en premier si nous trions lexicographiquement. Les chaînes sont comparées lexicographiquement avant d'être arrangées. Dans cet article, nous verrons différentes techniques pour comparer lexicographiquement deux chaînes en utilisant C++. Utilisation de la fonction compare() dans les chaînes C++ L'objet C++string a une fonction compare()
 Programme C pour trouver la longueur de la liste chaînée
Sep 07, 2023 pm 07:33 PM
Programme C pour trouver la longueur de la liste chaînée
Sep 07, 2023 pm 07:33 PM
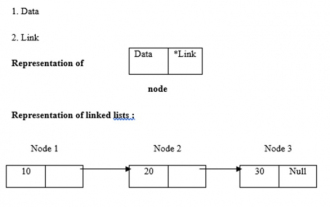
Les listes chaînées utilisent l’allocation dynamique de mémoire, c’est-à-dire qu’elles grandissent et diminuent en conséquence. Ils sont définis comme des collections de nœuds. Ici, un nœud comporte deux parties, des données et des liens. Les données, liens et listes chaînées sont représentés comme suit - Types de listes chaînées Il existe quatre types de listes chaînées, comme suit : - Liste chaînée simple / Liste chaînée simple Liste chaînée double / Double Liste chaînée simple circulaire Liste chaînée double circulaire Nous utilisons le méthode récursive pour trouver la longueur de la liste chaînée La logique est -intlength(node *temp){ if(temp==NULL) returnl{&n
 Le programme C utilise la fonction rename() pour changer le nom du fichier
Sep 21, 2023 pm 10:01 PM
Le programme C utilise la fonction rename() pour changer le nom du fichier
Sep 21, 2023 pm 10:01 PM
La fonction renommer modifie un fichier ou un répertoire de son ancien nom à son nouveau nom. Cette opération est similaire à l’opération de déplacement. Nous pouvons donc également utiliser cette fonction de renommage pour déplacer des fichiers. Cette fonction existe dans le fichier d'en-tête de la bibliothèque stdio.h. La syntaxe de la fonction rename est la suivante : intrename(constchar*oldname,constchar*newname); La fonction rename() accepte deux paramètres. L’un est l’ancien nom et l’autre le nouveau nom. Les deux paramètres sont des pointeurs vers des caractères constants qui définissent l'ancien et le nouveau nom du fichier. Renvoie zéro si le fichier a été renommé avec succès ; sinon, renvoie un entier différent de zéro. Lors d'une opération de changement de nom
 Programme C++ pour trouver la valeur de la fonction sinus hyperbolique inverse en prenant une valeur donnée comme argument
Sep 17, 2023 am 10:49 AM
Programme C++ pour trouver la valeur de la fonction sinus hyperbolique inverse en prenant une valeur donnée comme argument
Sep 17, 2023 am 10:49 AM
Les fonctions hyperboliques sont définies à l'aide d'hyperboles au lieu de cercles et sont équivalentes aux fonctions trigonométriques ordinaires. Il renvoie le paramètre de rapport dans la fonction sinus hyperbolique à partir de l'angle fourni en radians. Mais faites le contraire, ou en d’autres termes. Si nous voulons calculer un angle à partir d’un sinus hyperbolique, nous avons besoin d’une opération trigonométrique hyperbolique inverse comme l’opération sinus hyperbolique inverse. Ce cours montrera comment utiliser la fonction sinus hyperbolique inverse (asinh) en C++ pour calculer des angles en utilisant la valeur du sinus hyperbolique en radians. L'opération arc sinus hyperbolique suit la formule suivante -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Où\:In\:is\:logarithme naturel\:(log_e\:k)
 Programme C++ pour obtenir la partie imaginaire d'un nombre complexe donné
Sep 06, 2023 pm 06:05 PM
Programme C++ pour obtenir la partie imaginaire d'un nombre complexe donné
Sep 06, 2023 pm 06:05 PM
La science moderne s'appuie fortement sur le concept de nombres pluriels, qui a été établi pour la première fois au début du XVIIe siècle par Girolamo Cardano, qui l'a introduit au XVIe siècle. La formule pour les nombres complexes est a+ib, où a contient le code HTML et b est un nombre réel. Un nombre complexe est dit avoir deux parties : la partie réelle <a> et la partie imaginaire (<ib>). La valeur de i ou iota est √-1. La classe plurielle en C++ est une classe utilisée pour représenter des nombres complexes. La classe complexe en C++ peut représenter et contrôler plusieurs opérations sur les nombres complexes. Voyons comment représenter et contrôler l'affichage de nombres pluriels. Fonction membre imag() Comme mentionné ci-dessus, les nombres complexes sont composés d'une partie réelle et d'une partie imaginaire. Pour afficher la partie réelle, nous utilisons real()
 Programme C++ pour imprimer le dictionnaire
Sep 11, 2023 am 10:33 AM
Programme C++ pour imprimer le dictionnaire
Sep 11, 2023 am 10:33 AM
Une carte est un type spécial de conteneur en C++ où chaque élément est une paire de deux valeurs, à savoir une valeur clé et une valeur mappée. La valeur clé est utilisée pour indexer chaque élément et la valeur mappée est la valeur associée à la clé. Que la valeur mappée soit unique ou non, la clé est toujours unique. Pour imprimer des éléments de carte en C++, nous devons utiliser un itérateur. Un élément dans un ensemble d’éléments est indiqué par un objet itérateur. Les itérateurs sont principalement utilisés avec des tableaux et d'autres types de conteneurs (tels que des vecteurs), et ils disposent d'un ensemble spécifique d'opérations qui peuvent être utilisées pour identifier des éléments spécifiques dans une plage spécifique. Les itérateurs peuvent être incrémentés ou décrémentés pour référencer différents éléments présents dans une plage ou un conteneur. L'itérateur pointe vers l'emplacement mémoire d'un élément spécifique dans la plage. Imprimer une carte en C++ à l'aide d'itérateurs Voyons d'abord comment définir
 Programme C++ pour vérifier si un caractère est alphabétique ou non alphabétique
Sep 14, 2023 pm 03:37 PM
Programme C++ pour vérifier si un caractère est alphabétique ou non alphabétique
Sep 14, 2023 pm 03:37 PM
L'utilisation de chaînes ou de caractères est parfois très utile pour résoudre certains problèmes de programmation logique. Une chaîne est une collection de caractères, qui est un type de données de 1 octet utilisé pour contenir des symboles dans des valeurs ASCII. Les symboles peuvent être des lettres anglaises, des chiffres ou des caractères spéciaux. Dans cet article, nous apprendrons comment vérifier si un caractère est une lettre anglaise ou une lettre de l'alphabet en utilisant C++. Vérifier la fonction isalpha() Pour vérifier si un nombre est une lettre, nous pouvons utiliser la fonction isalpha() dans le fichier d'en-tête ctype.h. Cela prend un caractère en entrée et renvoie vrai s'il s'agit d'un alphabet, faux sinon. Examinons l'implémentation C++ suivante pour comprendre l'utilisation de cette fonction. La traduction chinoise de l'exemple est : montrer



