Définir le partitionnement est NP-complet

Traduisez le problème Set Parcel en chinois. Il s'agit d'un problème NP-complet. La tâche consiste à déterminer si un ensemble donné d'entiers positifs peut être divisé en deux sous-ensembles de telle sorte que leurs sommes soient égales. NP-complet signifie qu'aucun algorithme en temps polynomial actuellement connu ne peut résoudre tous les cas, et la vérification d'une solution possible doit être effectuée en temps polynomial. De nombreux autres problèmes NP-complets peuvent être réduits au problème Set Parcel, démontrant sa complexité informatique et son importance dans la compréhension de la classe plus large des problèmes NP-complets. En raison de sa complexité, la résolution de cas à grande échelle du problème Set Parcel peut nécessiter un investissement de temps considérable, ce qui rend difficile la recherche efficace d'une solution optimale.
Méthodes utilisées
Force Brute
Algorithme de retour en arrière
Force Brute
La force brute est une approche algorithmique simple et innocente pour résoudre un problème en évaluant toutes les permutations possibles et en choisissant la bonne. Cela implique d’énumérer efficacement toutes les permutations possibles et de vérifier réellement si chaque permutation répond aux exigences du problème. Bien que l’approche par force brute soit conceptuellement simple et facile à mettre en œuvre, elle peut s’avérer inefficace sur le plan informatique et peu pratique pour les problèmes liés aux grands espaces de permutation.
Indépendamment de sa simplicité, la puissance sauvage peut être une méthode importante pour les problèmes avec peu d'informations ou lorsque l'espace d'arrangement est généralement petit et raisonnable. Elle est régulièrement utilisée pour des problèmes simples, comme modèle pour confirmer l'exactitude ou comme étape de départ. avant d'appliquer des calculs plus modernes.
Algorithme
Calculez l'exhaustivité de tous les composants de l'ensemble et vérifiez s'ils sont divisibles par 2. Sinon, renvoyez "Aucune solution".
Initialisez deux ensembles de purge, subset1 et subset2.
Appelez l'assistant de partitionnement de travail récursif partitionHelper, en utilisant l'ensemble de départ S, le sous-ensemble 1, le sous-ensemble 2 et le total cible (totalSum / 2)
Dans la fonction partitionHelper :
Vérifiez si l'intégralité des composants du sous-ensemble 1 est égale à l'ensemble cible. Si tel est le cas, imprimez les sous-ensembles 1 et 2 et revenez. Si l'ensemble S est effacé, retournez Choisissez le composant x de S et expulsez-le de S.
Essayez d'inclure x dans le sous-ensemble1 et d'appeler partitionHelper de manière récursive avec le S, le sous-ensemble1, le sous-ensemble2 mis à niveau et la somme cible.
Si l'offre ne trouve pas de grande parcelle, excluez x du sous-ensemble 1 et essayez d'inclure x dans le sous-ensemble 2.
Appelez de manière récursive la fonction partitionHelper en utilisant le S réorganisé, le sous-ensemble 1, le sous-ensemble 2 et la somme cible
Si aucun segment substantiel n'est trouvé au milieu de la récursion, imprimez "Aucun arrangement".
Exemple
#include <iostream>
#include <vector>
bool partitionHelper(std::vector<int> S, std::vector<int>&
subset1, std::vector<int>& subset2, int targetSum) {
if (targetSum == 0) {
std::cout << "Subset 1: ";
for (int num : subset1) {
std::cout << num << " ";
}
std::cout << "\nSubset 2: ";
for (int num : subset2) {
std::cout << num << " ";
}
return true;
}
if (S.empty()) {
return false;
}
int x = S.back();
S.pop_back();
subset1.push_back(x);
if (partitionHelper(S, subset1, subset2, targetSum - x)) {
return true;
}
subset1.pop_back();
subset2.push_back(x);
if (partitionHelper(S, subset1, subset2, targetSum - x)) {
return true;
}
subset2.pop_back();
return false;
}
void partition(const std::vector<int>& S) {
int totalSum = 0;
for (int num : S) {
totalSum += num;
}
if (totalSum % 2 != 0) {
std::cout << "No solution.\n";
return;
}
std::vector<int> subset1, subset2;
int targetSum = totalSum / 2;
if (!partitionHelper(S, subset1, subset2, targetSum)) {
std::cout << "No solution.\n";
}
}
int main() {
std::vector<int> set = {1, 2, 3, 4, 5, 6};
partition(set);
return 0;
}
Sortie
No solution.
Retour en arrière
Le backtracking est une méthode algorithmique globale utilisée pour rechercher délibérément des réponses à des problèmes combinatoires. Il s'agit d'un type de recherche expérimentale dans laquelle le calcul étudie divers résultats imaginables, construisant progressivement un arrangement possible et faisant marche arrière lorsqu'il comprend que le flux et le reflux peuvent' Cela ne donne pas lieu à un arrangement substantiel.
Un système de backtracking peut être imaginé comme un arbre d'enquête, où chaque nœud représente une décision prise à une étape spécifique, et les branches représentent les résultats potentiels de cette décision. L'algorithme parcourt l'arbre en profondeur, explorant chaque chemin tour à tour jusqu'à ce qu'il trouve une solution valide ou épuise toutes les possibilités.
Algorithme
Commencez par deux ensembles vides, SetA et SetB, pour traiter les deux sous-ensembles en cours de mise en forme.
Étudiez de manière récursive tous les mélanges potentiels de composants d'un ensemble donné afin de vous rappeler ce qu'il y a dans SetA et SetB
À chaque étape, ajoutez un composant à SetA et récurez sur les composants supplémentaires, ou ajoutez-le à SetB et récurez
Surveillez le nombre de SetA et SetB pendant la récursion
Si à tout moment, le montant de SetA atteint le montant de SetB, ramenez Valid dans tous les cas, revenez Trompeur.
Example
#include <iostream>
#include <vector>
bool isValidSubset(const std::vector<int>& inputSet, int index, int
setSizeA, int setSizeB) {
if (index == inputSet.size()) {
return (setSizeA == setSizeB);
}
bool isValid = isValidSubset(inputSet, index + 1, setSizeA + 1, setSizeB);
isValid |= isValidSubset(inputSet, index + 1, setSizeA, setSizeB + 1);
return isValid;
}
int main() {
std::vector<int> inputSet = {1000, 2000, 3000, 4000, 5000};
bool isValid = isValidSubset(inputSet, 0, 0, 0);
std::cout << (isValid ? "Valid" : "Misleading") << std::endl;
return 0;
}
输出
Misleading
结论
本文研究了集合分割问题的NP完备性,该问题包括决定给定的一组正整数是否可以被分割成两个子集,使得它们的和相等。NP完备性意味着没有已知的多项式时间算法可以解决该问题的所有情况,并且验证一个潜在解决方案可以在多项式时间内完成。本文讨论了三种方法来解决这个问题:蛮力法、回溯法和动态规划。由于其复杂性,解决集合分割问题的大规模实例可能需要大量的时间和努力,使得寻找一个理想的解决方案变得具有挑战性。理解集合分割的复杂性很重要,因为它与其他NP完备问题相关,为我们揭示了计算复杂问题的更广泛教训
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
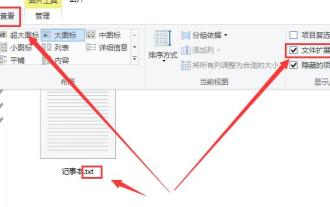 Comment changer l'extension de fichier du Bloc-notes Win10
Jan 04, 2024 pm 12:49 PM
Comment changer l'extension de fichier du Bloc-notes Win10
Jan 04, 2024 pm 12:49 PM
Lorsque nous utilisons le Bloc-notes, nous devons changer l'extension du Bloc-notes en raison de différentes choses que nous devons gérer. Alors, comment changer l'extension ? En fait, nous n'avons besoin que d'utiliser la fonction renommer pour modifier l'extension ? Comment changer l'extension du Bloc-notes Win10 : 1. Dans le dossier, cliquez d'abord en haut et cochez-le. 2. De cette façon, l'extension du fichier sera affichée, puis cliquez avec le bouton droit sur votre bloc-notes et sélectionnez 3. Sélectionnez Modifiez ce qui suit. 4. S'il est modifié au format .jpeg. Ensuite, une invite apparaîtra, cliquez dessus. 5. Le changement est terminé, et c’est tout.
 Appeler le déclencheur SQL pour exécuter un programme externe
Feb 18, 2024 am 10:25 AM
Appeler le déclencheur SQL pour exécuter un programme externe
Feb 18, 2024 am 10:25 AM
Titre : Exemples de code spécifiques permettant aux déclencheurs SQL d'appeler des programmes externes Texte : Lors de l'utilisation de déclencheurs SQL, il est parfois nécessaire d'appeler des programmes externes pour traiter certaines opérations spécifiques. Cet article explique comment appeler des programmes externes dans des déclencheurs SQL et donne des exemples de code spécifiques. 1. Créer un déclencheur Tout d'abord, nous devons créer un déclencheur pour écouter un événement dans la base de données. Ici, nous prenons comme exemple la "table de commande (order_table)" Lorsqu'une nouvelle commande est insérée, le déclencheur sera activé, puis le programme externe sera appelé pour effectuer une opération.
 Comment convertir du HTML au format MP4
Feb 19, 2024 pm 02:48 PM
Comment convertir du HTML au format MP4
Feb 19, 2024 pm 02:48 PM
Titre : Comment convertir du HTML au format MP4 : Exemple de code détaillé Dans le processus quotidien de production Web, nous rencontrons souvent le besoin de convertir des pages HTML ou des éléments HTML spécifiques en vidéos MP4. Par exemple, enregistrez des effets d'animation, des diaporamas ou d'autres éléments dynamiques sous forme de fichiers vidéo. Cet article explique comment utiliser HTML5 et JavaScript pour convertir du HTML au format MP4 et fournit des exemples de code spécifiques. Balise vidéo HTML5 et introduction à CanvasAPI HTML5
 Comment extraire les fichiers Dump
Feb 19, 2024 pm 12:15 PM
Comment extraire les fichiers Dump
Feb 19, 2024 pm 12:15 PM
Comment récupérer les fichiers Dump Dans un système informatique, un fichier Dump est un fichier qui enregistre l'état de fonctionnement et les données du système. Dans le développement de logiciels et le dépannage du système, la récupération des fichiers Dump peut aider les développeurs de programmes et les administrateurs système à analyser et à diagnostiquer divers problèmes, tels que les plantages de programmes, les fuites de mémoire et les anomalies du système. Cet article présentera quelques méthodes et outils courants pour récupérer les fichiers Dump. 1. Comment récupérer les fichiers Dump sous le système Windows à l'aide du Gestionnaire des tâches : Dans le système d'exploitation Windows,
 Quel est le rôle du panneau de configuration NVIDIA ?
Feb 19, 2024 pm 03:59 PM
Quel est le rôle du panneau de configuration NVIDIA ?
Feb 19, 2024 pm 03:59 PM
Qu'est-ce que le panneau de configuration NVIDIA ? Avec le développement rapide de la technologie informatique, l'importance des cartes graphiques est devenue de plus en plus importante. En tant que l'un des principaux fabricants de cartes graphiques au monde, le panneau de configuration de NVIDIA a attiré encore plus d'attention. Alors, que fait exactement le panneau de configuration NVIDIA ? Cet article vous donnera une introduction détaillée aux fonctions et utilisations du panneau de configuration NVIDIA. Tout d'abord, comprenons le concept et la définition du panneau de configuration NVIDIA. Le panneau de configuration NVIDIA est un logiciel utilisé pour gérer et configurer les paramètres liés à la carte graphique.
 Comment ouvrir des fichiers psd sur un téléphone mobile
Feb 21, 2024 pm 05:48 PM
Comment ouvrir des fichiers psd sur un téléphone mobile
Feb 21, 2024 pm 05:48 PM
Les fichiers PSD des téléphones mobiles sont ouverts à l'aide du logiciel Photoshop. PSD est le format de fichier propriétaire de Photoshop et peut conserver des informations telles que les calques, les canaux, les chemins, la transparence, etc. Par conséquent, si vous souhaitez ouvrir un fichier PSD pour téléphone mobile, assurez-vous d’abord d’avoir installé le logiciel Photoshop. Tout d'abord, ouvrez le logiciel Photoshop, puis cliquez sur l'option "Fichier" dans la barre de menu et sélectionnez "Ouvrir" dans le menu déroulant contextuel. Ensuite, vous devez parcourir vos dossiers pour trouver le téléphone sur lequel vous avez enregistré
 Date de sortie de Windows 12
Jan 05, 2024 pm 05:24 PM
Date de sortie de Windows 12
Jan 05, 2024 pm 05:24 PM
Auparavant, Win11 était officiellement publié et de nombreux utilisateurs ont déjà commencé à profiter de Win12. Ils veulent savoir quand Win12 sortira. En fait, selon les règles, il sortira vers 2024. Quand Win12 est-il sorti : R : Win12 devrait être publié vers l’automne 2024. 1. Selon les dernières informations de Microsoft, Win12 devrait sortir à l’automne 2024. 2. Et cette fois, win12 aura plusieurs nouveaux concepts de conception, et il y aura davantage d'améliorations en termes de netteté et d'apparence visuelle. 3. Lors de la dernière réunion des développeurs, les développeurs de Microsoft ont révélé qu'ils créeraient une barre des tâches flottante pour donner à la barre des tâches une sensation de flottement.
 Le rôle de la pleine largeur et de la demi-largeur dans la méthode de saisie chinoise
Mar 25, 2024 am 09:57 AM
Le rôle de la pleine largeur et de la demi-largeur dans la méthode de saisie chinoise
Mar 25, 2024 am 09:57 AM
La pleine largeur et la demi-largeur sont des concepts courants dans les méthodes de saisie chinoises et représentent différentes largeurs de caractères. Dans le domaine informatique, les notions de pleine largeur et de demi-largeur sont principalement utilisées pour décrire la taille de l'espace occupé par les caractères chinois et les lettres anglaises à l'écran ou sur papier. Tout d’abord, la pleine largeur et la demi-largeur sont originaires de l’ère des machines à écrire. Sur les machines à écrire, les caractères chinois sont généralement affichés en pleine largeur, tandis que les caractères anglais sont affichés en demi-largeur. En effet, les caractères chinois sont relativement larges et l'utilisation de la pleine largeur peut rendre l'article entier plus beau et la mise en page plus compacte. Les caractères anglais sont






