
En C++, un trie est une structure de données de haut niveau utilisée pour stocker une collection d'arbres. Le mot trie vient du mot récupération, on l'appelle arbre de nombres ou arbre de préfixes.
Prenons un exemple de toutes les jointures possibles en prenant une liste de chaînes donnée.
Nous définissons l'entrée de chaîne comme {"tutor", "true", "tuo"}
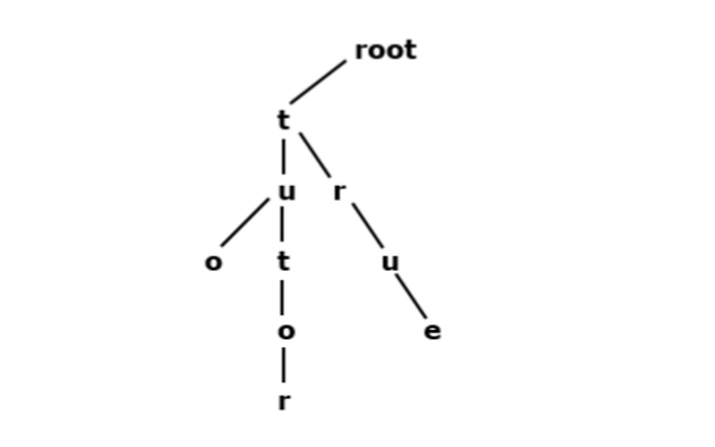
On peut observer que différentes chaînes sont concaténées en une seule chaîne. Voici donc t et u sont des listes de caractères concaténant toutes les chaînes possibles.
Dans cet article, nous utiliserons la structure de données trie pour résoudre toutes les concaténations possibles dans une liste de chaînes.
1 2 3 |
|
struct - Ce mot-clé est utilisé pour représenter le type de données de structure.
name_of_structure − Nous fournissons n'importe quel nom pour la structure.
Une structure est un ensemble de diverses variables liées en un seul endroit.
1 |
|
alpha est le nom de la variable pointant vers le pointeur de structure/membre de données nommé treetrie. alphabet est une macro qui définit la valeur totale des caractères, exprimée sous forme d'entier.
Nous utilisons d'abord un fichier d'en-tête nommé 'bits/stdc++.h', qui contient toutes les bibliothèques de modèles standards du C++.
Nous définissons deux macros, 'alphabet' et 'max', qui définissent le nombre total de caractères dans l'alphabet et la valeur maximale des caractères.
Nous créons une structure appelée ‘tree node’ et définissons un pointeur vers ‘tree_node’ pour stocker l’adresse de la lettre. Définissez la variable 'end_word' en utilisant le type de données bool, qui sera utilisé pour le caractère de fin de la chaîne.
Nous utilisons un pointeur pour nous connecter à un nouveau nœud représentant l'arbre construit par le trie, définissant une fonction appelée 'buildNode'.
Pour insérer une chaîne, nous avons créé une fonction récursive appelée 'ins_recursive_of_string' qui accepte trois paramètres - itm, str (la chaîne à insérer), i (représentant le caractère en cours de traitement).
ins() est définie dans le code comme une fonction wrapper de ins_recursive_of_str(). Il accepte deux paramètres : tree_trie* itm (un objet tree_trie) et string str (la chaîne à insérer). Il appelle la fonction récursive en utilisant le nœud actuel, la chaîne à insérer et l'index de départ 0.
Ensuite, nous créons une fonction appelée LeafNode() qui accepte un objet tree_trie comme paramètre et vérifie s'il s'agit d'un nœud feuille, c'est-à-dire s'il n'a pas d'enfants.
fonction display_joint() est définie dans le code et accepte quatre paramètres : tree_trie* root, tree_trie* itm (le nœud en cours de traitement), char str[] (un tableau de caractères str, pour Stores la chaîne de chemin formée du nœud racine au nœud actuel) et un niveau int (un niveau entier représentant la profondeur du nœud actuel).
Ce code définit la fonction displayJ(), qui est une fonction wrapper pour display_joint(). Il accepte un objet tree_trie comme argument et appelle la fonction display_joint() avec le nœud racine, un tableau de caractères vide et un niveau de départ de 0 comme arguments.
Ce code définit la fonction main(), qui génère un nouvel objet tree_trie en tant que nœud racine Trie. Il génère un vecteur s contenant une liste de chaînes à insérer dans le Trie. Ensuite, il appelle la fonction ins() pour insérer chaque chaîne dans le Trie.
Enfin, il imprime un message pour indiquer le début de la sortie et appelle la fonction displayJ() pour afficher tous les points de jointure Trie.
Dans ce programme, nous imprimerons tous les points de jointure possibles d'un trie construit à partir d'une liste de chaînes donnée.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 |
|
1 2 3 |
|
Nous avons exploré le concept de structure de données trie, où nous avons construit tous les points de jointure trie possibles à partir d'une liste donnée de chaînes. Nous voyons dans le résultat que les caractères u et t connectent tous les points de connexion possibles du trie en utilisant des chaînes telles que tutor, true et tuo. Un arbre peut donc réduire ses nœuds en donnant des points de connexion possibles.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Comment désactiver l'invite de mise à niveau Win10
Comment désactiver l'invite de mise à niveau Win10
 La différence entre les serveurs d'applications légers et les serveurs cloud
La différence entre les serveurs d'applications légers et les serveurs cloud
 Commande de fermeture du port CMD
Commande de fermeture du port CMD
 La différence entre l'écran externe et l'écran interne cassé
La différence entre l'écran externe et l'écran interne cassé
 Comment sauter avec des paramètres dans vue.js
Comment sauter avec des paramètres dans vue.js
 Somme de cellule
Somme de cellule
 Comment intercepter les appels harcelants
Comment intercepter les appels harcelants
 monnaie numérique virtuelle
monnaie numérique virtuelle