 développement back-end
développement back-end
 Tutoriel Python
Tutoriel Python
 Comment implémenter un algorithme de descente de gradient en Python pour trouver les minima locaux ?
Comment implémenter un algorithme de descente de gradient en Python pour trouver les minima locaux ?
Comment implémenter un algorithme de descente de gradient en Python pour trouver les minima locaux ?
La descente de gradient est une méthode d'optimisation importante dans l'apprentissage automatique, utilisée pour minimiser la fonction de perte du modèle. En termes simples, cela nécessite de modifier à plusieurs reprises les paramètres du modèle jusqu'à ce que la plage de valeurs idéale qui minimise la fonction de perte soit trouvée. La méthode fonctionne en faisant de petits pas dans la direction du gradient négatif de la fonction de perte, ou plus précisément, le long du chemin de descente la plus raide. Le taux d'apprentissage est un hyperparamètre qui régule le compromis entre la vitesse et la précision de l'algorithme, et il affecte la taille du pas. De nombreuses méthodes d'apprentissage automatique, notamment la régression linéaire, la régression logistique et les réseaux de neurones, pour n'en citer que quelques-unes, utilisent la descente de gradient. Sa principale application est la formation de modèles, où l'objectif est de minimiser la différence entre les valeurs attendues et réelles de la variable cible. Dans cet article, nous examinerons l'implémentation de la descente de gradient en Python pour trouver les minimums locaux.
Il est maintenant temps d'implémenter la descente de gradient en Python. Voici une explication de base de la façon dont nous le mettons en œuvre -
Tout d’abord, nous importons les bibliothèques nécessaires.
Définir sa fonction et ses dérivées.
Ensuite, nous appliquerons la fonction de descente de gradient.
Après avoir appliqué la fonction, nous définirons les paramètres pour trouver le minimum local,
Enfin, nous tracerons la sortie.
Implémentation de la descente de dégradé en Python
Importer une bibliothèque
import numpy as np import matplotlib.pyplot as plt
Ensuite on définit la fonction f(x) et sa dérivée f'(x) -
def f(x): return x**2 - 4*x + 6 def df(x): return 2*x - 4
F(x) est la fonction qui doit être réduite et df est sa dérivée (x). La méthode de descente de gradient utilise des dérivées pour se guider vers le minimum en révélant la pente de la fonction en cours de route.
Définissez ensuite la fonction de descente de gradient.
def gradient_descent(initial_x, learning_rate, num_iterations):
x = initial_x
x_history = [x]
for i in range(num_iterations):
gradient = df(x)
x = x - learning_rate * gradient
x_history.append(x)
return x, x_history
x, le taux d'apprentissage et le nombre d'itérations requis sont envoyés à la fonction de descente de gradient. Pour enregistrer la valeur de x après chaque itération, il initialise x à sa valeur d'origine et génère une liste vide. Le procédé effectue ensuite une descente de gradient pour le nombre d'itérations fourni, en modifiant x à chaque itération selon l'équation x = x - taux d'apprentissage * gradient. Cette fonction génère une liste de valeurs x pour chaque itération et la valeur finale de x.
La fonction de descente de gradient peut désormais être utilisée pour localiser le minimum local de f(x) -
Exemple
initial_x = 0
learning_rate = 0.1
num_iterations = 50
x, x_history = gradient_descent(initial_x, learning_rate, num_iterations)
print("Local minimum: {:.2f}".format(x))
Sortie
Local minimum: 2.00
Dans cette figure, x est initialement défini sur 0, le taux d'apprentissage est de 0,1 et 50 itérations sont exécutées. Enfin, nous publions la valeur de x, qui doit être proche du minimum local à x=2.
Tracer la fonction f(x) et la valeur x pour chaque itération nous permet de voir le processus de descente de gradient en action -
Exemple
# Create a range of x values to plot
x_vals = np.linspace(-1, 5, 100)
# Plot the function f(x)
plt.plot(x_vals, f(x_vals))
# Plot the values of x at each iteration
plt.plot(x_history, f(np.array(x_history)), 'rx')
# Label the axes and add a title
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')
# Show the plot
plt.show()
Sortie
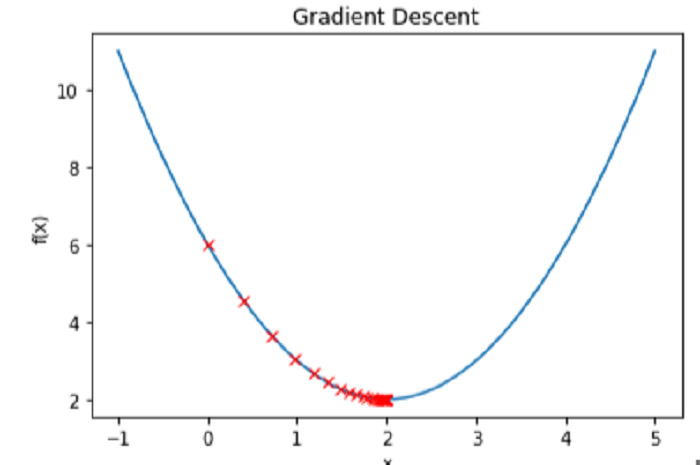
Conclusion
En résumé, pour trouver le minimum local d'une fonction, Python utilise un processus d'optimisation efficace appelé descente de gradient. La descente de gradient fonctionne en calculant la dérivée d'une fonction à chaque étape, en mettant à jour à plusieurs reprises les valeurs d'entrée dans la direction de la descente la plus raide jusqu'à ce que la valeur la plus basse soit atteinte. L'implémentation de la descente de gradient en Python nécessite de spécifier la fonction à optimiser et ses dérivées, d'initialiser les valeurs d'entrée et de déterminer le taux d'apprentissage et le nombre d'itérations de l'algorithme. Une fois l'optimisation terminée, la méthode peut être évaluée en traçant ses étapes au minimum et en voyant comment elle atteint cet objectif. La descente de gradient est une technique utile dans les applications d'apprentissage automatique et d'optimisation, car Python peut gérer de grands ensembles de données et des fonctions complexes.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment les plumes PS contrôlent-elles la douceur de la transition?
Apr 06, 2025 pm 07:33 PM
Comment les plumes PS contrôlent-elles la douceur de la transition?
Apr 06, 2025 pm 07:33 PM
La clé du contrôle des plumes est de comprendre sa nature progressive. Le PS lui-même ne fournit pas la possibilité de contrôler directement la courbe de gradient, mais vous pouvez ajuster de manière flexible le rayon et la douceur du gradient par plusieurs plumes, des masques correspondants et des sélections fines pour obtenir un effet de transition naturel.
 MySQL doit-il payer
Apr 08, 2025 pm 05:36 PM
MySQL doit-il payer
Apr 08, 2025 pm 05:36 PM
MySQL a une version communautaire gratuite et une version d'entreprise payante. La version communautaire peut être utilisée et modifiée gratuitement, mais le support est limité et convient aux applications avec des exigences de stabilité faibles et des capacités techniques solides. L'Enterprise Edition fournit une prise en charge commerciale complète pour les applications qui nécessitent une base de données stable, fiable et haute performance et disposées à payer pour le soutien. Les facteurs pris en compte lors du choix d'une version comprennent la criticité des applications, la budgétisation et les compétences techniques. Il n'y a pas d'option parfaite, seulement l'option la plus appropriée, et vous devez choisir soigneusement en fonction de la situation spécifique.
 Comment utiliser MySQL après l'installation
Apr 08, 2025 am 11:48 AM
Comment utiliser MySQL après l'installation
Apr 08, 2025 am 11:48 AM
L'article présente le fonctionnement de la base de données MySQL. Tout d'abord, vous devez installer un client MySQL, tel que MySQLWorkBench ou le client de ligne de commande. 1. Utilisez la commande MySQL-UROot-P pour vous connecter au serveur et connecter avec le mot de passe du compte racine; 2. Utilisez Createdatabase pour créer une base de données et utilisez Sélectionner une base de données; 3. Utilisez CreateTable pour créer une table, définissez des champs et des types de données; 4. Utilisez InsertInto pour insérer des données, remettre en question les données, mettre à jour les données par mise à jour et supprimer les données par Supprimer. Ce n'est qu'en maîtrisant ces étapes, en apprenant à faire face à des problèmes courants et à l'optimisation des performances de la base de données que vous pouvez utiliser efficacement MySQL.
 Comment configurer des plumes de PS?
Apr 06, 2025 pm 07:36 PM
Comment configurer des plumes de PS?
Apr 06, 2025 pm 07:36 PM
La plume PS est un effet flou du bord de l'image, qui est réalisé par la moyenne pondérée des pixels dans la zone de bord. Le réglage du rayon de la plume peut contrôler le degré de flou, et plus la valeur est grande, plus elle est floue. Le réglage flexible du rayon peut optimiser l'effet en fonction des images et des besoins. Par exemple, l'utilisation d'un rayon plus petit pour maintenir les détails lors du traitement des photos des caractères et l'utilisation d'un rayon plus grand pour créer une sensation brumeuse lorsque le traitement de l'art fonctionne. Cependant, il convient de noter que trop grand, le rayon peut facilement perdre des détails de bord, et trop petit, l'effet ne sera pas évident. L'effet de plumes est affecté par la résolution de l'image et doit être ajusté en fonction de la compréhension de l'image et de la saisie de l'effet.
 Comment optimiser les performances de la base de données après l'installation de MySQL
Apr 08, 2025 am 11:36 AM
Comment optimiser les performances de la base de données après l'installation de MySQL
Apr 08, 2025 am 11:36 AM
L'optimisation des performances MySQL doit commencer à partir de trois aspects: configuration d'installation, indexation et optimisation des requêtes, surveillance et réglage. 1. Après l'installation, vous devez ajuster le fichier my.cnf en fonction de la configuration du serveur, tel que le paramètre innodb_buffer_pool_size, et fermer query_cache_size; 2. Créez un index approprié pour éviter les index excessifs et optimiser les instructions de requête, telles que l'utilisation de la commande Explication pour analyser le plan d'exécution; 3. Utilisez le propre outil de surveillance de MySQL (ShowProcessList, Showstatus) pour surveiller la santé de la base de données, et sauvegarde régulièrement et organisez la base de données. Ce n'est qu'en optimisant en continu ces étapes que les performances de la base de données MySQL peuvent être améliorées.
 Le fichier de téléchargement MySQL est endommagé et ne peut pas être installé. Réparer la solution
Apr 08, 2025 am 11:21 AM
Le fichier de téléchargement MySQL est endommagé et ne peut pas être installé. Réparer la solution
Apr 08, 2025 am 11:21 AM
Le fichier de téléchargement mysql est corrompu, que dois-je faire? Hélas, si vous téléchargez MySQL, vous pouvez rencontrer la corruption des fichiers. Ce n'est vraiment pas facile ces jours-ci! Cet article expliquera comment résoudre ce problème afin que tout le monde puisse éviter les détours. Après l'avoir lu, vous pouvez non seulement réparer le package d'installation MySQL endommagé, mais aussi avoir une compréhension plus approfondie du processus de téléchargement et d'installation pour éviter de rester coincé à l'avenir. Parlons d'abord de la raison pour laquelle le téléchargement des fichiers est endommagé. Il y a de nombreuses raisons à cela. Les problèmes de réseau sont le coupable. L'interruption du processus de téléchargement et l'instabilité du réseau peut conduire à la corruption des fichiers. Il y a aussi le problème avec la source de téléchargement elle-même. Le fichier serveur lui-même est cassé, et bien sûr, il est également cassé si vous le téléchargez. De plus, la numérisation excessive "passionnée" de certains logiciels antivirus peut également entraîner une corruption des fichiers. Problème de diagnostic: déterminer si le fichier est vraiment corrompu
 MySQL ne peut pas être installé après le téléchargement
Apr 08, 2025 am 11:24 AM
MySQL ne peut pas être installé après le téléchargement
Apr 08, 2025 am 11:24 AM
Les principales raisons de la défaillance de l'installation de MySQL sont les suivantes: 1. Problèmes d'autorisation, vous devez s'exécuter en tant qu'administrateur ou utiliser la commande sudo; 2. Des dépendances sont manquantes et vous devez installer des packages de développement pertinents; 3. Conflits du port, vous devez fermer le programme qui occupe le port 3306 ou modifier le fichier de configuration; 4. Le package d'installation est corrompu, vous devez télécharger et vérifier l'intégrité; 5. La variable d'environnement est mal configurée et les variables d'environnement doivent être correctement configurées en fonction du système d'exploitation. Résolvez ces problèmes et vérifiez soigneusement chaque étape pour installer avec succès MySQL.
 Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Comment optimiser les performances MySQL pour les applications de haute charge?
Apr 08, 2025 pm 06:03 PM
Guide d'optimisation des performances de la base de données MySQL dans les applications à forte intensité de ressources, la base de données MySQL joue un rôle crucial et est responsable de la gestion des transactions massives. Cependant, à mesure que l'échelle de l'application se développe, les goulots d'étranglement des performances de la base de données deviennent souvent une contrainte. Cet article explorera une série de stratégies efficaces d'optimisation des performances MySQL pour garantir que votre application reste efficace et réactive dans des charges élevées. Nous combinerons des cas réels pour expliquer les technologies clés approfondies telles que l'indexation, l'optimisation des requêtes, la conception de la base de données et la mise en cache. 1. La conception de l'architecture de la base de données et l'architecture optimisée de la base de données sont la pierre angulaire de l'optimisation des performances MySQL. Voici quelques principes de base: sélectionner le bon type de données et sélectionner le plus petit type de données qui répond aux besoins peut non seulement économiser un espace de stockage, mais également améliorer la vitesse de traitement des données.





