numéro du dodécagone central

Les nombres graphiques qui représentent un dodécagone sont appelés nombres dodécagonaux. Le numéro du dodécagone central est représenté par un point au centre et d'autres points entourant ce point dans une couche de dodécagones continus (c'est-à-dire des polygones à 12 côtés).

Le numéro du dodécagone central peut être mieux expliqué par l'image ci-dessous.

Pour n=1, il n’y a qu’un seul point au centre. La sortie est donc 1.

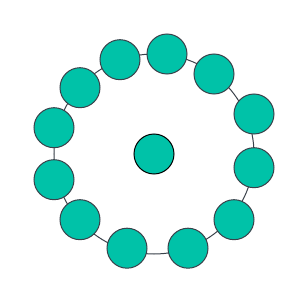
Pour n=2, il y a un point au centre entouré d'un dodécagone. Le nombre total de points sera donc de 13. Le prochain numéro du dodécagone central sera donc 13.

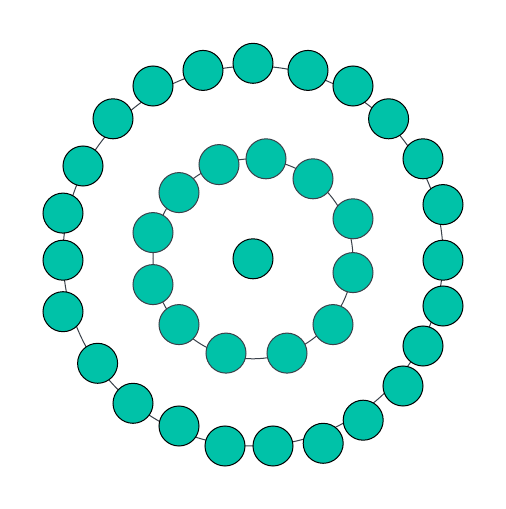
Pour n=3, il y aura un seul point au centre, suivi d'un dodécagone qui l'entoure, puis de la couche consécutive suivante de dodécagones contenant 24 points. Par conséquent, le nombre total de points sera de 37, ce qui sera le prochain numéro du dodécagone central.

De même, cela s’ensuit pour tout nombre positif n. En référence à cela, les premiers nombres du dodécagone seront 1, 13, 37, 73, 121, 181…..

Dans ce problème, nous recevrons n'importe quel nombre positif n et devrons imprimer le nième numéro du dodécagone central.

Par exemple,

Entrez - 2

Sortie - 13

Entrez - 5

Sortie - 121

Voici l'algorithme pour résoudre ce problème.

Algorithme

Pour calculer le nième nombre du dodécagone central, nous devons comprendre le modèle suivi dans le problème.

Selon la notion de numéro dodécagone central, il est représenté par un point au centre puis des couches successives de dodécagones. Les couches dodécagonales successives sont 12, 24, 36, 48... Si l'on regarde bien le motif, il forme une suite arithmétique avec une tolérance de 12.

Puisque les premières séquences de nombres du dodécagone central sont 1, 13, 37, 73…. Ce n'est rien de plus que la somme des couches du dodécagone et d'un point au centre.

On peut mieux le comprendre si l'on considère une séquence de couches dodécagonales consécutives commençant par 0.

0, 12, 24, 36, 48.
For n=1, the centred dodecagonal number is 1 which is 0+1.
For n=2, the centred dodecagonal number is 13 which is 0+12+1.
For n=3, the centred dodecagonal number is 37 which is 0+12+24+1.

À partir de là, nous pouvons penser que le nième nombre du dodécagone central n'est rien d'autre que la somme des A.P. de n termes commençant à 0 avec la tolérance étant de 12 et 1.

Ainsi, la formule du nième nombre du dodécagone central peut être exprimée comme suit :

$$mathrm{CDn=séquence arithmétique (a=0 : somme : d=12) : de : somme des n premiers termes : +1}$$

$$mathrm{CD_n:=:frac{n}{2}(2a:+:(n-1)d):+1}$$

Ici, $mathrm{CD_n}$ est le nième numéro du dodécagone central

a est le premier terme de la suite arithmétique, qui est 0

d est la tolérance de la suite arithmétique, qui est 12

De plus, la formule peut s'écrire comme suit :

$$mathrm{CD_n:=:frac{12n}{2}(n-1):+:1}$$

$$mathrm{CD_n:=:6n(n-1):+:1}$$

Conserver le texte original sans traduction

Nous utiliserons la formule ci-dessus pour calculer le nième nombre du dodécagone central dans notre méthode.

Méthode

• Pour résoudre ce problème, nous créons simplement une fonction pour calculer le nième nombre du dodécagone central.

• Nous utiliserons la formule dérivée ci-dessus pour calculer le nième nombre du dodécagone central pour n nombres positifs.

• Renvoyer la valeur calculée, qui sera notre résultat souhaité.

La traduction chinoise de

Exemple

est :

Exemple

Ce qui suit est l'implémentation de la méthode ci-dessus en C++ -

#include <iostream>
#include<bits/stdc++.h>

using namespace std;

//function to calculate the nth centred dodecagonal number
int CDn(int N){
   int ans= 6 * N * (N-1) + 1; //used to store nth centred dodecagonal number value
   
   return ans; //return the answer
}
int main(){
   int N=8;
   cout<<CDn(N)<<endl;
   
   N=6;
   cout<<CDn(N)<<endl;
   
   N=12;
   cout<<CDn(N)<<endl;
   
   return 0;
}

Sortie

337
181
793

Complexité temporelle : O(1), car un temps constant est requis.

Complexité spatiale : O(1) puisque nous ne prenons pas d’espace supplémentaire.

Conclusion

Dans cet article, nous avons résolu le problème de l’impression du nième nombre dodécagone centré. Nous avons appris le concept des nombres dodécagones centrés et avons dérivé la formule du nième nombre,

J'espère que vous avez trouvé cet article utile pour comprendre et clarifier tous les concepts concernant ce problème.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!