 développement back-end
développement back-end
 C++
C++
 Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud

BST ou Binary Search Tree est une forme d'arbre binaire dans lequel tous les nœuds de gauche ont des valeurs inférieures à la valeur du nœud racine et tous les nœuds de droite ont des valeurs supérieures à la valeur du nœud racine. Pour ce problème, nous prendrons un arbre binaire et y ajouterons toutes les valeurs supérieures à la valeur actuelle du nœud. Le problème "ajouter toutes les valeurs plus grandes à chaque nœud d'un BST" est simplifié pour, pour un BST, ajouter toutes les valeurs de nœud supérieures à la valeur de nœud actuelle à cette valeur de nœud.
Ajoutez tous les nœuds de valeur plus grande à chaque nœud dans l'énoncé du problème BST :
Étant donné un arbre de recherche binaire (BST), nous devons ajouter pour chaque nœud la somme de tous les nœuds de valeur plus grande.
Input
10
/ \
/ \
5 20
/ \ / \
1 7 1 5Output
70
/ \
82 45
/ \ / \
83 77 60 25Explication
Ce programme convertira un arbre de recherche binaire en un arbre binaire où la valeur d'un nœud est la somme de tous les éléments plus grands plus la valeur d'origine du nœud.
Ajoutez toutes les valeurs plus grandes à chaque nœud dans la solution de l'arbre de recherche binaire :
Nous utilisons le parcours inverse dans l'ordre (appelant récursivement le sous-arbre droit en premier au lieu du sous-arbre gauche) et maintenons une variable pour stocker la somme des nœuds qui ont été parcourues jusqu'à présent.
Nous utilisons ensuite cette somme pour modifier la valeur du nœud actuel, en ajoutant d'abord sa valeur à la somme, puis en remplaçant la valeur du nœud par cette somme.
Exemple
#include <iostream >
using namespace std;
struct node {
int data;
node *left;
node *right;
};
node *newNode(int key) {
node *temp=new node;
temp->left=NULL;
temp->right=NULL;
temp->data=key;
return temp;
}
void Inorder(node *root) {
if(!root)
return;
Inorder(root->left);
cout<<root->data<<" ";
Inorder(root->right);
}
node *Insert(node *root,int key) {
if(!root)
return newNode(key);
if(key<root->data)
root->left=Insert(root->left,key);
else
root->right=Insert(root->right,key);
return root;
}
void RevInorderAdd(node *root,int &sum) {
if(!root)
return;
RevInorderAdd(root->right,sum);
sum+=root->data;
root->data=sum;
RevInorderAdd(root->left,sum);
}
void AddGreater(node *root) {
int sum=0;
RevInorderAdd(root,sum);
}
int main() {
/* Let us create following BST
10
/ \
5 20
/ \ / \
1 7 15 25 */
node *root = NULL;
root = Insert(root, 10);
Insert(root, 20);
Insert(root, 25);
Insert(root, 15);
Insert(root, 5);
Insert(root, 7);
Insert(root, 1);
Inorder(root);
cout<<endl;
AddGreater(root);
Inorder(root);
cout<<endl;
return 0;
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Interrogez le poids minimum dans le sous-arbre à partir du nœud X et la distance au plus D
Aug 25, 2023 am 11:25 AM
Interrogez le poids minimum dans le sous-arbre à partir du nœud X et la distance au plus D
Aug 25, 2023 am 11:25 AM
Lors de la programmation informatique, il est parfois nécessaire de trouver le poids minimum d'un sous-arbre provenant d'un nœud spécifique, à condition que le sous-arbre ne puisse pas contenir de nœuds éloignés de plus de D unités du nœud spécifié. Ce problème se pose dans divers domaines et applications, notamment la théorie des graphes, les algorithmes arborescents et l'optimisation des réseaux. Un sous-arbre est un sous-ensemble d'une structure arborescente plus grande, le nœud spécifié servant de nœud racine du sous-arbre. Un sous-arbre contient tous les descendants du nœud racine et leurs arêtes de connexion. Le poids d'un nœud fait référence à une valeur spécifique attribuée à ce nœud, qui peut représenter son importance, sa signification ou d'autres mesures pertinentes. Dans ce problème, l’objectif est de trouver le poids minimum parmi tous les nœuds d’un sous-arbre tout en limitant le sous-arbre aux nœuds situés au plus à D unités du nœud racine. Dans l'article suivant, nous approfondirons la complexité de l'extraction des poids minimum des sous-arbres.
 Code C++ pour inverser les chemins dans un arbre de recherche binaire à l'aide de files d'attente
Sep 14, 2023 pm 07:21 PM
Code C++ pour inverser les chemins dans un arbre de recherche binaire à l'aide de files d'attente
Sep 14, 2023 pm 07:21 PM
Par exemple, étant donné un arbre de recherche binaire, nous devons inverser son chemin à partir d'une clé spécifique. Façons de trouver la solution Dans cette approche, nous allons créer une file d'attente et pousser tous les nœuds jusqu'à ce que nous obtenions le nœud racine. p>Exemple #include<bits/stdc++.h>usingnamespacestd;structnode{ intkey; structnode*left,*right;};structnode*newNode(intitem){&nb
 Comment implémenter les fonctions de copie et de coupure de nœuds des cartes mentales via Vue et jsmind ?
Aug 15, 2023 pm 05:57 PM
Comment implémenter les fonctions de copie et de coupure de nœuds des cartes mentales via Vue et jsmind ?
Aug 15, 2023 pm 05:57 PM
Comment implémenter les fonctions de copie et de coupure de nœuds des cartes mentales via Vue et jsmind ? La carte mentale est un outil de réflexion courant qui peut nous aider à organiser nos pensées et à trier notre logique de pensée. Les fonctions de copie et de coupe de nœuds sont des opérations couramment utilisées dans les cartes mentales, qui nous permettent de réutiliser plus facilement les nœuds existants et d'améliorer l'efficacité de l'organisation de la réflexion. Dans cet article, nous utiliserons les deux outils Vue et jsmind pour implémenter les fonctions de copie et de coupe de nœuds de la carte mentale. Tout d'abord, nous devons installer Vue et jsmind et créer
 Comment implémenter un arbre de recherche binaire en Python
Jun 10, 2023 am 08:57 AM
Comment implémenter un arbre de recherche binaire en Python
Jun 10, 2023 am 08:57 AM
Binary Search Tree (BST) est un algorithme de recherche basé sur des arbres binaires. Sa caractéristique est que la valeur dans le sous-arbre gauche de chaque nœud de l'arbre est inférieure à la valeur de ce nœud, tandis que la valeur dans le sous-arbre droit est supérieure à la valeur de ce nœud. Par conséquent, la complexité temporelle des opérations de recherche et d’insertion BST est O(logN). La méthode d'implémentation d'un arbre de recherche binaire en Python est relativement simple, car Python possède deux structures de données intégrées, des listes et des dictionnaires, qui peuvent toutes deux être utilisées pour implémenter des arbres binaires. ici
 Tas binaire et arbre de recherche binaire en C++
Aug 22, 2023 pm 04:10 PM
Tas binaire et arbre de recherche binaire en C++
Aug 22, 2023 pm 04:10 PM
En programmation C++, le tas binaire et l'arbre de recherche binaire sont deux structures de données couramment utilisées. Elles présentent des similitudes, mais elles présentent également des différences. Cet article présentera respectivement les concepts, les opérations de base et les scénarios d'application des tas binaires et des arbres de recherche binaires. 1. Concept du tas binaire 1.1 Le tas binaire est un arbre binaire complet qui satisfait aux deux propriétés suivantes : 1.1.1 Ordre du tas L'ordre du tas signifie que dans un tas binaire, la valeur de chaque nœud n'est pas supérieure (ou inférieure) à la valeur de son nœud parent. Ici, nous prenons le tas maximum comme exemple, c'est-à-dire que la valeur du nœud racine est la plus grande valeur de tout l'arbre, et
 Quelle est la méthode pour supprimer un nœud dans js
Sep 01, 2023 pm 05:00 PM
Quelle est la méthode pour supprimer un nœud dans js
Sep 01, 2023 pm 05:00 PM
Les méthodes de suppression de nœuds dans js sont : 1. La méthode removeChild() est utilisée pour supprimer le nœud enfant spécifié du nœud parent. Elle nécessite deux paramètres. Le premier paramètre est le nœud enfant à supprimer et le deuxième paramètre est. le nœud parent. 2. La méthode parentNode.removeChild() peut être appelée directement via le nœud parent pour supprimer le nœud enfant ; 3. La méthode remove() peut supprimer directement le nœud sans spécifier le nœud parent ; L'attribut innerHTML est utilisé pour supprimer le contenu du nœud.
 Trouvez le chemin le plus court entre deux nœuds à l'aide de l'algorithme Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
Trouvez le chemin le plus court entre deux nœuds à l'aide de l'algorithme Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
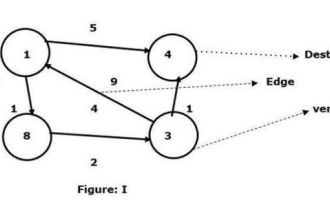
C++ a une macro, qui est définie comme un morceau de code ou une valeur attendue, et elle sera réutilisée chaque fois que l'utilisateur en aura besoin. L'algorithme de Floyd-Walshall est le processus permettant de trouver le chemin le plus court entre toutes les paires de sommets dans un graphe pondéré donné. L'algorithme suit une approche de programmation dynamique pour trouver le graphique de poids minimum. Comprenons la signification de l'algorithme de Floyd-Walshall à travers un diagramme - prenons le sommet 1 comme source et le sommet 4 comme destination et trouvons le chemin le plus court entre eux. Nous avons vu qu'il existe deux chemins qui peuvent être connectés au sommet cible 4. 1->4 – l'arête a un poids de 51->8->3->4 – le poids de l'arête (1+2+1) est 4. Dans le graphique I donné, nous voyons la plus petite arête reliant deux sommets. Voici donc le sommet
 Java utilise la fonction max() de la classe Math pour obtenir le plus grand de deux nombres
Jul 24, 2023 pm 11:17 PM
Java utilise la fonction max() de la classe Math pour obtenir le plus grand de deux nombres
Jul 24, 2023 pm 11:17 PM
Java utilise la fonction max() de la classe Math pour obtenir la plus grande valeur de deux nombres. En programmation Java, nous devons souvent comparer les tailles de deux nombres, puis sélectionner le plus grand nombre pour effectuer certaines opérations. La classe Math en Java fournit de nombreuses fonctions pour les opérations mathématiques, parmi lesquelles la fonction max() peut nous aider à obtenir la plus grande valeur de deux nombres. La fonction Math.max() est définie comme suit : publicstaticintmax(inta,intb) Cette fonction accepte deux entiers





