Exprimer la factorielle n comme la somme de nombres consécutifs

Nous aborderons deux méthodes pour découvrir comment exprimer la factorielle d'un nombre comme la somme de nombres consécutifs. La première méthode est la méthode directe et simple, tandis que dans l'autre méthode nous utilisons le concept de progression arithmétique pour la rendre moins complexe en termes de temps et d'espace occupé.
Énoncé du problème
Étant donné un nombre, nous devons trouver un moyen d'exprimer la factorielle du nombre comme la somme de nombres naturels consécutifs.
Cela implique deux fonctions différentes -
Trouvez la factorielle d'un nombre.
Trouvez le nombre de façons dont un nombre peut être exprimé comme la somme de nombres naturels consécutifs.
Exemple 1
Given : Number = 3 Result: 1
Nous savons tous que la factorielle de 3 est 6, qui peut s'écrire 1+2+3, donc notre réponse est : 1 voie.
Exemple 2
Given: Number = 4 Result: 1
Comme nous le savons tous, la factorielle de 4 est 24, ce qui peut s'écrire 7+8+9, donc notre réponse est : 1 voie.
Méthode 1
Il s'agit d'une méthode simple où nous trouvons d'abord la factorielle d'un nombre, puis calculons le nombre de façons dont il peut être exprimé comme la somme de nombres naturels consécutifs. La méthode consiste à exprimer la factorielle sous la forme d'une série de longueur arithmétique len+1 sous la forme -
Factorial of Number = p + (p+1) + (p+2) + … + (p+len) So, p = (Number- len*(len+1)/2)/(len+1) We will check for the values of len from 1 to len*(len+1)/2<Number
Lorsque nous obtenons len sous forme d'entier positif, nous le considérons comme une solution.
Exemple
Dans l'exemple ci-dessous, nous essayons de trouver le nombre de façons d'exprimer la factorielle d'un nombre comme la somme de nombres consécutifs.
#include <bits/stdc++.h>
using namespace std;
// code for obtaining number of possible solutions
long int Number_of_solutions(long int NUMBER){
long int counter = 0;
for (long int len = 1; len * (len + 1) < 2 * NUMBER; len++) {
double p = (1.0 * NUMBER - (len * (len + 1)) / 2) / (len + 1);
if (p - (int)p == 0.0)
counter++;
}
return counter;
}
// main program goes here
int main(){
long int NUMBER = 15;
cout << "Number of ways to write 15 as a sum of consecutive numbers: ";
cout << Number_of_solutions(NUMBER) << endl;
NUMBER = 10;
cout << "Number of ways to write 10 as a sum of consecutive numbers: ";
cout << Number_of_solutions(NUMBER) << endl;
return 0;
}
Sortie
Lorsque vous exécutez le programme C++ ci-dessus, il produira le résultat suivant :
Number of ways to write 15 as a sum of consecutive numbers: 3 Number of ways to write 10 as a sum of consecutive numbers: 1
Méthode 2 : Méthode d'optimisation
C'est une meilleure approche ; l'approche que nous avons vue ci-dessus provoque un débordement.
La somme de len nombres consécutifs à partir du nombre p peut s'écrire -
sum = (p+1) + (p+2) + (p+3) … + (p+len) Hence, sum = (len*(len + 2*p + 1))/2
Parce que sum est également égal au Nombre !.
Nous pouvons écrire
2*Number! = (len*(len + 2*p + 1))
Ici, au lieu de compter toutes les paires (len, p), nous compterons toutes les paires (len, (len + 2*p + 1)). Cela signifie que nous calculerons tous les pf ordonnés (A, B) où AB=2*Number ! Et A< B 且 A 和 B 的奇偶性不同,这意味着如果 len 是奇数,则 (len + 2*p + 1) 是偶数,如果 len 是偶数,则 (len + 2*p + 1) 是奇数。
Cela signifie que nous recherchons des diviseurs impairs de 2*Nombre ! C'est aussi le diviseur impair du Nombre !
Calculez le nombre de diviseurs ! , il faut calculer les puissances des nombres premiers en factorisation, le nombre de diviseurs est (f1 + 1)*(f2 + 1)* … *(fn + 1).
Nous utiliserons la formule de Legendre pour calculer la puissance maximale d'un nombre premier dans la factorielle d'un nombre.
Exemple
Le code de cette approche est donné ci-dessous -
#include <bits/stdc++.h>
using namespace std;
#define maximum 5002
vector<int> v;
void sieve(){
bool Is_the_number_prime[maximum];
memset (Is_the_number_prime, true, sizeof(Is_the_number_prime) );
for (int prime = 2; prime * prime < maximum; prime++) {
if (Is_the_number_prime[prime] == true) {
for (int iterator = prime * 2; iterator < maximum; iterator += prime)
Is_the_number_prime[iterator] = false;
}
}
for (int prime = 2; prime < maximum; prime++)
if (Is_the_number_prime[prime])
v.push_back(prime);
}
long long int calculate_largest_power(long long int a, long long int b){
long long int c = 0;
long long int x = b;
while (a >= x) {
c += (a / x);
x *= b;
}
return c;
}
long long int modular_mult(long long int a,
long long int b,
long long int m){
long long int result = 0;
a = a % m;
while (b > 0) {
if (b % 2 == 1)
result = (result + a) % m;
a = (a * 2) % m;
b /= 2;
}
return result % m;
}
long long int no_of_ways(long long int n,
long long int m){
long long int answer = 1;
for (int iterator = 1; iterator < v.size(); iterator++) {
long long int powers = calculate_largest_power(n, v[iterator]);
if (powers == 0)
break;
answer = modular_mult(answer, powers + 1, m)%m;
}
if (((answer - 1) % m) < 0)
return (answer - 1 + m) ;
else
return (answer - 1) ;
}
int main(){
sieve();
long long int n = 4, m = 7;
cout << "Number of solutions after performing modulo with 7 is " <<no_of_ways(n, m);
return 0;
}
Sortie
Lorsque le programme C++ ci-dessus est exécuté, il produira le résultat suivant :
Number of solutions after performing modulo with 7 is 1.
Conclusion
Dans cet article, nous avons discuté de deux manières différentes de connaître la factorielle d'un nombre comme la somme de nombres naturels consécutifs.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Somme absolue de tuples en Python
Sep 12, 2023 pm 07:37 PM
Somme absolue de tuples en Python
Sep 12, 2023 pm 07:37 PM
En Python, les tuples sont des séquences immuables pouvant stocker plusieurs éléments de types différents. Ils sont souvent utilisés pour représenter des collections de valeurs liées. La sommation de tuples consiste à ajouter les éléments correspondants de deux ou plusieurs tuples pour produire un nouveau tuple. Cependant, dans certains scénarios, il peut être nécessaire de calculer la somme absolue des éléments au lieu de la somme traditionnelle. Dans cet article de blog, nous explorerons comment effectuer des sommes absolues de tuples en Python. Somme de tuples traditionnelle Avant de nous plonger dans la somme de tuples absolue, comprenons d'abord comment faire une somme de tuples traditionnelle. Étant donné deux tuples de même longueur, nous pouvons utiliser une simple boucle Python ou une compréhension de liste pour calculer la somme des éléments correspondants −deftuple_sum(t1,t2) :
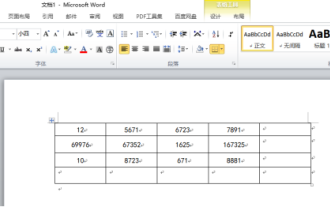 Savez-vous comment résumer un tableau Word ?
Mar 21, 2024 pm 01:10 PM
Savez-vous comment résumer un tableau Word ?
Mar 21, 2024 pm 01:10 PM
Parfois, nous rencontrons souvent des problèmes de comptage dans les tableaux Word. Généralement, lorsqu'ils rencontrent de tels problèmes, la plupart des étudiants copient le tableau Word dans Excel pour le calcul ; certains étudiants prennent silencieusement la calculatrice. Existe-t-il un moyen rapide de le calculer ? Bien sûr, la somme peut également être calculée dans Word. Alors, savez-vous comment faire ? Aujourd’hui, jetons un coup d’œil ensemble ! Sans plus attendre, les amis dans le besoin devraient rapidement le récupérer ! Détails de l'étape : 1. Tout d'abord, nous ouvrons le logiciel Word sur l'ordinateur et ouvrons le document qui doit être traité. (Comme le montre l'image) 2. Ensuite, nous plaçons le curseur sur la cellule où se trouve la valeur additionnée (comme le montre l'image), puis nous cliquons sur [Barre de menu) ;
 Trouver la somme d'une séquence arithmétique de signes décalés
Sep 16, 2023 pm 05:01 PM
Trouver la somme d'une séquence arithmétique de signes décalés
Sep 16, 2023 pm 05:01 PM
Une progression arithmétique (PA) est une suite de nombres dans laquelle la différence entre deux termes consécutifs est la même. La différence est calculée en soustrayant le deuxième terme du premier terme. Comprenons AP avec un exemple de séquence, 5,7,9,11,13,15,... La tolérance (d) de cette série arithmétique est de 2. Cela signifie que chaque élément suivant diffère de l’élément précédent de 2. Le premier élément (a) de cette séquence est 5. La formule générale pour trouver le nième terme est a{n}=a+(n-1)(d) Dans ce problème, on nous donne un AP et nous devons trouver la somme d'une série de carrés signés alternés, la série sera Comme indiqué ci-dessous, a12-a22+a32-a42+a52+... Prenons un exemple pour une compréhension plus claire&
 Trouver la somme des éléments d'un tableau en utilisant la fonction array_sum() en PHP
Nov 18, 2023 am 11:20 AM
Trouver la somme des éléments d'un tableau en utilisant la fonction array_sum() en PHP
Nov 18, 2023 am 11:20 AM
Titre : Recherchez la somme des éléments d'un tableau à l'aide de la fonction array_sum() en PHP. PHP est un langage de script côté serveur largement utilisé. Il fournit de nombreuses fonctions intégrées qui peuvent simplifier le processus de développement et améliorer l'efficacité. Parmi elles, la fonction array_sum() est une fonction très pratique qui permet de calculer la somme des éléments d'un tableau. Dans cet article, nous allons apprendre à utiliser la fonction array_sum() et donner des exemples de code spécifiques. Tout d’abord, nous devons comprendre l’utilisation de la fonction array_sum()
 Comment additionner automatiquement les totaux dans Excel
Mar 20, 2024 pm 12:20 PM
Comment additionner automatiquement les totaux dans Excel
Mar 20, 2024 pm 12:20 PM
Pour les utilisateurs qui utilisent souvent des tableaux Excel, la fonction de somme automatique est une opération très simple, et elle peut automatiquement additionner jusqu'à plusieurs décimales selon nos besoins, ce qui est bien plus pratique que d'appuyer manuellement sur la calculatrice. Pour les utilisateurs novices, vous devez encore apprendre à additionner automatiquement les totaux dans Excel à partir de zéro. Jetons un coup d'œil aux étapes : Somme automatique Excel : Tout d'abord, nous devons ajouter les nombres dans les cellules A1 et B1, puis afficher les résultats dans. cellule C1. Pour ce faire, entrez d'abord les nombres que vous souhaitez ajouter dans les cellules A1 et B1. Ensuite, sélectionnez la cellule C1 et entrez la formule suivante : `=A1+B1` Après avoir appuyé sur la touche Entrée, la cellule C1 affichera la somme des nombres dans les cellules A1 et B1.
 Comment utiliser la fonction de tableau du langage Go pour additionner et renvoyer le résultat ?
Jul 31, 2023 pm 02:25 PM
Comment utiliser la fonction de tableau du langage Go pour additionner et renvoyer le résultat ?
Jul 31, 2023 pm 02:25 PM
Comment utiliser la fonction de tableau du langage Go pour additionner et renvoyer le résultat ? Le langage Go fournit une multitude de fonctions d'opération sur les tableaux, y compris des fonctions permettant de trouver la somme des éléments du tableau. Utilisez ces fonctions pour effectuer facilement des opérations de somme sur des tableaux et renvoyer les résultats. Cet article explique comment utiliser la fonction tableau du langage Go pour additionner et renvoyer le résultat, avec des exemples de code. Tout d’abord, jetons un coup d’œil aux tableaux en langage Go. Un tableau est une structure de données qui stocke une séquence d'éléments de taille fixe. En langage Go, la longueur du tableau est fixe, ainsi que le type et l'élément du tableau
 Comment utiliser la formule de sommation Excel - tutoriel sur la façon d'utiliser la formule de sommation Excel
Mar 05, 2024 pm 12:40 PM
Comment utiliser la formule de sommation Excel - tutoriel sur la façon d'utiliser la formule de sommation Excel
Mar 05, 2024 pm 12:40 PM
De nombreux amis ne savent toujours pas comment utiliser la formule de sommation dans Excel, c'est pourquoi l'éditeur ci-dessous explique le didacticiel sur la façon d'utiliser la formule de sommation dans Excel. Si vous en avez besoin, veuillez y jeter un œil. tout le monde. Étape 1 : Nous ouvrons d’abord Excel (comme indiqué sur l’image). Étape 2 : Entrez dans l'interface de travail Excel (comme indiqué sur l'image). Étape 3 : Ensuite, nous ouvrons le document qui doit être modifié. Voici un exemple de document (comme indiqué sur l'image). Étape 4 : Sélectionnez « Score total » et entrez « = C2+D2+E2 » dans la zone de fonction fx. Appuyez ensuite sur la touche Entrée. Le score total est sorti (comme le montre l'image). Étape 5 : Cliquez sur le menu déroulant de la zone de remplissage. Remplissez le score total (comme indiqué sur la figure). Étape 6 : Remplissez le menu déroulant (comme indiqué sur l'image). Étape 7 :
 Programme Java pour imprimer la somme des nombres
Aug 20, 2023 am 09:49 AM
Programme Java pour imprimer la somme des nombres
Aug 20, 2023 am 09:49 AM
Il existe différentes manières d'ajouter des nombres en Java. Les nombres à ajouter peuvent être saisis lors de l'exécution ou directement dans le programme. Cependant, il est difficile d'ajouter des nombres de cette manière si la liste des nombres est trop grande. Parfois, les données à ajouter sont données dans une feuille de calcul Excel.






