
Lorsque l'hypoténuse (H) du triangle rectangle est donnée, utilisez la formule πH2/4 pour trouver l'aire du cercle circonscrit du triangle rectangle.
Cette formule est dérivée en exploitant le fait que le cercle circonscrit touche tous les angles d'un triangle, en l'occurrence la longueur maximale entre deux points hypothétiques passant par le centre du cercle. Cela fait de l'hypoténuse le diamètre du cercle.
C'est pourquoi l'aire d'un cercle est πd2/4. (d = 2r) Remplacez d par H.
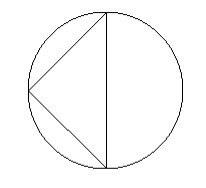
Hypoténuse = 8
Zone du cercle = 50,26
Démonstration en direct
#include <stdio.h>
int main(void) {
int H = 14;
float pie = 3.14;
float area = (float)((pie*H*H)/4);
printf("the area of circumcircle of a right angled triangle of Hypotenuse %d is %f",H,area);
return 0;
}the area of circumcircle of a right angled triangle of Hypotenuse 14 is 153.860016
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!