 développement back-end
développement back-end
 C++
C++
 Écrit en C++, trouvez le nombre de sous-tableaux dont la somme est inférieure à K
Écrit en C++, trouvez le nombre de sous-tableaux dont la somme est inférieure à K
Écrit en C++, trouvez le nombre de sous-tableaux dont la somme est inférieure à K

Dans cet article, nous trouverons le nombre de sous-tableaux dont la somme est inférieure à K en utilisant C++. Dans ce problème, nous avons un tableau arr[] et un entier K. Nous devons maintenant trouver les sous-tableaux dont la somme est inférieure à K. Vous trouverez ci-dessous l'exemple −
Input : arr[] = {1, 11, 2, 3, 15}
K = 10
Output : 4
{1}, {2}, {3} and {2, 3}Façon de trouver la solution
Nous allons maintenant utiliser deux méthodes différentes pour résoudre le problème donné -
Force brute
Dans cette méthode, nous allons parcourir tous les sous-tableaux et calculer leur somme et si la somme est inférieure à k, comparez avec k pour augmenter notre réponse.
Exemple
#include <bits/stdc++.h>
using namespace std;
int main(){
int arr[] = {1, 11, 2, 3, 15}; // given array
int k = 10; // given k
int size = sizeof(arr) / sizeof(int); // size of our array.
int ans = 0; // counter variable.
for(int i = 0; i < size; i++){ // outer loop.
int sum = 0;
for(int j = i; j < size; j++){ // inner loop.
sum = sum + arr[j];
if(sum < k) // comparing with k.
ans++; // incrementing our ans if sum is less than k.
}
}
cout << ans << "\n";
return 0;
}Sortie
4
Cependant, cette méthode n'est pas très bonne car sa complexité temporelle est très élevée O(N*N), où n est la taille du tableau.
Nous rechercherons des solutions alternatives en utilisant une approche de fenêtre glissante (cela nous aidera à réduire la complexité temporelle du programme).
Méthode efficace
Contrairement à la force brute
méthode efficace
strong>, nous ne parcourons pas tous les sous-tableaux. Au lieu de cela, seulement lorsque la somme des sous-tableaux dépasse k , nous itérons et déplaçons la limite gauche vers la limite droite et répétons jusqu'à ce que tout le tableau soit parcouru.
Exemple
#include <bits/stdc++.h>
using namespace std;
int main(){
int arr[] = {1, 11, 2, 3, 15}; // given array
int k = 10; // given k
int size = sizeof(arr) / sizeof(int); // size of our array.
int ans = 0; // counter variable.
int start = 0; // left border.
int end = 0; // right border.
int sum = 0;
while(end < size && start < size){ // till the whole array is traversed.
while(sum >= k && start < end){
sum = sum - arr[start];
start++;
}
if(end >= start)
ans = ans + end - start;
sum += arr[end];
end++;
}
cout << ans << "\n";
return 0;
}Sortie
4
Nous utilisons la Technique de fenêtre coulissante pour rendre notre programme plus rapide ou plus efficace face à des contraintes plus importantes.
Explication du code ci-dessus
Dans cette approche, nous itérons généralement jusqu'à ce que notre somme soit inférieure à k et incrémentons notre réponse en fonction de celle-ci, c'est le changement clé dans le code qui se produit lorsque la somme est supérieure ou égale à k . Dans ce cas, nous commençons à incrémenter notre limite gauche jusqu'à ce qu'elle soit inférieure ou égale à k ou que la somme soit supérieure ou égale à k. Au fur et à mesure que notre traitement progresse, il parcourt d'autres sous-réseaux possibles qui peuvent être formés. La somme de ces nouveaux sous-tableaux inférieure à k est ajoutée à notre réponse, donc notre réponse est incrémentée.
Par rapport à la solution de force brute précédente, cette méthode est très efficace car sa complexité temporelle est O(N), où N est la taille de notre tableau.
Conclusion
Dans cet article, nous avons résolu le problème de trouver le nombre de sous-tableaux dont la somme est inférieure à k en utilisant la technique de la fenêtre coulissante. Nous avons également appris un programme C++ pour ce problème et notre approche complète pour le résoudre (à la fois triviale et efficace). Nous pouvons écrire le même programme dans d'autres langages comme C, Java, Python et autres. J'espère que cet article vous sera utile.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1359
1359
 52
52
 Utilisez C++ pour écrire du code afin de trouver le Nième nombre non carré
Aug 30, 2023 pm 10:41 PM
Utilisez C++ pour écrire du code afin de trouver le Nième nombre non carré
Aug 30, 2023 pm 10:41 PM
Nous connaissons tous des nombres qui ne sont le carré d’aucun nombre, comme 2, 3, 5, 7, 8, etc. Il existe N nombres non carrés et il est impossible de connaître tous les nombres. Ainsi, dans cet article, nous expliquerons tout sur les nombres sans carrés ou non carrés et les moyens de trouver le Nième nombre non carré en C++. Nième nombre non carré Si un nombre est le carré d'un entier, alors ce nombre est appelé un carré parfait. Quelques exemples de nombres carrés parfaits sont -1iscarréde14iscarréde29iscarréde316iscarréde425iscarréde5 Si un nombre n'est le carré d'aucun entier, alors le nombre est appelé non carré. Par exemple, les 15 premiers nombres non carrés sont -2,3,5,6,
 Algorithme d'inversion pour la rotation à droite du tableau écrit en C++
Sep 08, 2023 pm 08:17 PM
Algorithme d'inversion pour la rotation à droite du tableau écrit en C++
Sep 08, 2023 pm 08:17 PM
Dans cet article, nous découvrirons l'algorithme d'inversion pour faire pivoter le tableau donné vers la droite de k éléments, par exemple −Input:arr[]={4,6,2,6,43,7,3,7}, k= 4Sortie :{43,7,3,7,4,6,2,6}Explication : La rotation de chaque élément du tableau par 4 éléments vers la droite donne{43,7,3,7,4,6,2,6}.Entrée :arr[]= {8 ,5,8,2,1,4,9,3},k=3Sortie :{4,9,3,8,5,8,2,1} Trouver la solution
 En programmation C, trouver l'aire d'un cercle
Aug 25, 2023 pm 10:57 PM
En programmation C, trouver l'aire d'un cercle
Aug 25, 2023 pm 10:57 PM
Un cercle est une figure fermée. Tous les points d'un cercle sont équidistants d'un point à l'intérieur du cercle. Le point central est appelé le centre du cercle. La distance d’un point au centre d’un cercle s’appelle le rayon. L'aire est une représentation quantitative de l'étendue des dimensions d'une figure fermée. L'aire d'un cercle est l'aire délimitée par les dimensions du cercle. La formule pour calculer l'aire d'un cercle, Aire=π*r*r Pour calculer l'aire, nous donnons le rayon du cercle en entrée, nous utiliserons la formule pour calculer l'aire, algorithme ÉTAPE 1 : Prendre le rayon comme entrée de l'utilisateur utilisant st dinput.ÉTAPE 2 : Calculez l'aire du cercle en utilisant, aire = (
 Trouver le nombre de paires uniques dans un tableau en utilisant C++
Sep 07, 2023 am 11:53 AM
Trouver le nombre de paires uniques dans un tableau en utilisant C++
Sep 07, 2023 am 11:53 AM
Nous avons besoin de connaissances appropriées pour créer plusieurs paires uniques dans la syntaxe des tableaux de C++. Tout en trouvant le nombre de paires uniques, nous comptons toutes les paires uniques dans le tableau donné, c'est-à-dire que toutes les paires possibles peuvent être formées où chaque paire doit être unique. Par exemple -Input:array[]={5,5,9}Output:4Explication:Thenumberoffalluniquepairsare(5,5),(5,9),(9,5)and(9,9).Input:array[] = {5,4,3,2,2}Sortie : 16 façons de trouver une solution Il existe deux façons de résoudre ce problème, ce sont -
 En Java, recherchez la somme maximale des sous-tableaux après avoir divisé un tableau en sous-tableaux en fonction d'une requête donnée.
Aug 29, 2023 am 11:21 AM
En Java, recherchez la somme maximale des sous-tableaux après avoir divisé un tableau en sous-tableaux en fonction d'une requête donnée.
Aug 29, 2023 am 11:21 AM
Nous avons deux tableaux d'entiers, l'un avec les éléments calculés et l'autre avec les points de division nécessaires pour diviser le tableau afin de générer des sous-ensembles, nous devons calculer la somme de chaque sous-ensemble dans chaque division et renvoyer le sous-ensemble maximum. Passons en revue l'exemple Comprendre : - input −intarr[]=intarr[]={9,4,5,6,7}intsplitPoints[]={0,2,3,1} ; sortie−la somme maximale du sous-tableau après chaque division [ 22, 13,9,9] Explication - Ici, nous décomposons le tableau en fonction de ses points de division et obtenons le sous-ensemble maximum après chaque division et après la première division → {9} et {4,5,6,7 }>> La somme maximale des sous-tableaux est de -22 après la deuxième division →{9},{4
 Écrivez un code en C++ pour trouver le nombre de sous-tableaux avec les mêmes valeurs minimales et maximales
Aug 25, 2023 pm 11:33 PM
Écrivez un code en C++ pour trouver le nombre de sous-tableaux avec les mêmes valeurs minimales et maximales
Aug 25, 2023 pm 11:33 PM
Dans cet article, nous utiliserons C++ pour résoudre le problème de trouver le nombre de sous-tableaux dont les valeurs maximales et minimales sont les mêmes. Voici un exemple du problème −Input:array={2,3,6,6,2,4,4,4}Output:12Explication :{2},{3},{6},{6}, {2 },{4},{4},{4},{6,6},{4,4},{4,4}et{4,4,4}sont les sous-tableaux qui peuvent être formés avec les mêmes éléments maximum et minimum. Entrée : tableau = {3, 3, 1,5,
 Inverser le regroupement de listes doublement chaînées par taille donnée en utilisant C++
Sep 04, 2023 am 09:49 AM
Inverser le regroupement de listes doublement chaînées par taille donnée en utilisant C++
Sep 04, 2023 am 09:49 AM
Dans ce problème, on nous donne un pointeur vers la tête de la liste chaînée et un entier k. Dans un groupe de taille k, nous devons inverser la liste chaînée. Par exemple -Input:1<->2<->3<->4<->5(doublelylinkedlist),k=3Output:3<->2<->1<->5<->4 à la recherche de solutions Méthode Dans ce problème, nous formulerons un algorithme récursif pour résoudre ce problème. Dans cette méthode, nous utiliserons la récursivité et résoudrons le problème en utilisant la récursivité. Exemple#include<iostream&
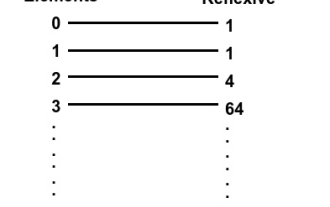 Écrit en C++, trouver le nombre de relations réflexives sur un ensemble
Aug 26, 2023 pm 08:17 PM
Écrit en C++, trouver le nombre de relations réflexives sur un ensemble
Aug 26, 2023 pm 08:17 PM
Dans cet article, nous expliquerons comment trouver des relations réflexives sur un ensemble. Dans ce problème, on nous donne un nombre n et un ensemble de n nombres naturels, et nous devons déterminer le nombre de relations réflexives. Relation réflexive - Une relation R est dite être une relation réflexive sur l'ensemble A si pour chaque 'a' dans l'ensemble A, (a, a) appartient à la relation R. Par exemple -Input:x=1Output:1Explanation:set={1},reflexiverelationsonA*A:{{1}}Input:x=2Output:4Explanation:set={1,2},reflexiverelationsonA*



