Programme C++ pour calculer la somme des diagonales d'une matrice

L'utilisation de tableaux ou de matrices bidimensionnels est extrêmement avantageuse pour plusieurs les applications. Les lignes et les colonnes matricielles sont utilisées pour contenir des nombres. Nous pouvons définir la 2D. Les tableaux multidimensionnels sont utilisés pour représenter des matrices en C++. Dans cet article, nous verrons comment mettre en œuvre utilisez C++ pour calculer la somme diagonale d'une matrice carrée donnée.
Les matrices ont deux diagonales, la diagonale principale et la diagonale secondaire (parfois appelées diagonales majeures et mineures). La diagonale majeure commence en haut à gauche. coin (index [0, 0]) vers le coin inférieur droit (index [n-1, n-1]) où n est l'ordre des Matrice carrée. La diagonale principale commence au coin supérieur droit (index [n-1, 0]) et se termine au coin inférieur gauche coin (index [0, n-1]). Voyons l'algorithme pour trouver la somme des éléments avec ces deux diagonales.
La traduction chinoise deMatrix Diagonal Sum
est :La somme des diagonales de la matrice
$$commencer{bmatrix} 8&5&3nouvelle ligne 6 & 7 & 1nouvelle ligne 2 & 4 & 9 fin{bmatrix},$$
Sum of all elements in major diagonal: (8 + 7 + 9) = 24 Sum of all elements in minor diagonal: (3 + 7 + 2) = 12
Dans l'exemple précédent, une matrice 3 x 3 a été utilisée. Nous avons scanné les diagonales. individuellement et calculé la somme. Voyons l'algorithme et la mise en œuvre pour un aperçu clair. vue.
Algorithme
- Lire la matrice M en entrée
- Considérez M avec n lignes et n colonnes
- sum_major := 0
- sum_minor := 0
- Pour la plage de i de 0 à n-1, exécutez
- pour j compris entre 0 et n - 1, faites
- si i et j sont identiques, alors
- sum_major := sum_major + M[ i ][ j ]
- fin si
- si (i + j) est identique à (N - 1), alors
- sum_minor := sum_minor + M[ i ][ j ]
- fin si
- si i et j sont identiques, alors
- fin pour
- fin pour
- somme de retour
Exemple
#include <iostream>
#include <cmath>
#define N 7
using namespace std;
float solve( int M[ N ][ N ] ){
int sum_major = 0;
int sum_minor = 0;
for ( int i = 0; i < N; i++ ) {
for ( int j = 0; j < N; j++ ) {
if( i == j ) {
sum_major = sum_major + M[ i ][ j ];
}
if( (i + j) == N - 1) {
sum_minor = sum_minor + M[ i ][ j ];
}
}
}
cout << "The sum of major diagonal: " << sum_major << endl;
cout << "The sum of minor diagonal: " << sum_minor << endl;
}
int main(){
int mat1[ N ][ N ] = {
{5, 8, 74, 21, 69, 78, 25},
{48, 2, 98, 6, 63, 52, 3},
{85, 12, 10, 6, 9, 47, 21},
{6, 12, 18, 32, 5, 10, 32},
{8, 45, 74, 69, 1, 14, 56},
{7, 69, 17, 25, 89, 23, 47},
{98, 23, 15, 20, 63, 21, 56},
};
cout << "For the first matrix: " << endl;
solve( mat1 );
int mat2[ N ][ N ] = {
{6, 8, 35, 21, 87, 8, 26},
{99, 2, 36, 326, 25, 24, 56},
{15, 215, 3, 157, 8, 41, 23},
{96, 115, 17, 5, 3, 10, 18},
{56, 4, 78, 5, 10, 22, 58},
{85, 41, 29, 65, 47, 36, 78},
{12, 23, 87, 45, 69, 96, 12}
};
cout << "\nFor the second matrix: " << endl;
solve( mat2 );
}
Sortie
For the first matrix: The sum of major diagonal: 129 The sum of minor diagonal: 359 For the second matrix: The sum of major diagonal: 74 The sum of minor diagonal: 194
Conclusion
Dans cet article, nous avons vu comment calculer les sommes diagonales d'une matrice carrée donnée. La diagonale principale s'étend du coin supérieur gauche au coin inférieur droit, tandis que la diagonale secondaire s'étend du coin inférieur gauche au coin supérieur droit. La ligne diagonale part du coin supérieur droit jusqu'au coin inférieur gauche. Pour trouver la somme de ceux-ci éléments diagonaux, nous parcourons tous les éléments lorsque les valeurs d'index de ligne et de colonne. Idem, il représente l'élément diagonal principal lorsque la somme des deux indices est Identique à l'ordre n-1 de la matrice, il sera ajouté à la sous-diagonale La procédure prend deux boucles imbriquées et nous parcourons tous les éléments présents dans le Tableau 2D. Par conséquent, calculer la somme de deux diagonales prendra un temps O(n2) matrice donnée.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment faire de Google Maps la carte par défaut sur iPhone
Apr 17, 2024 pm 07:34 PM
Comment faire de Google Maps la carte par défaut sur iPhone
Apr 17, 2024 pm 07:34 PM
La carte par défaut sur l'iPhone est Maps, le fournisseur de géolocalisation propriétaire d'Apple. Même si la carte s’améliore, elle ne fonctionne pas bien en dehors des États-Unis. Il n'a rien à offrir par rapport à Google Maps. Dans cet article, nous discutons des étapes réalisables pour utiliser Google Maps afin de devenir la carte par défaut sur votre iPhone. Comment faire de Google Maps la carte par défaut sur iPhone Définir Google Maps comme application cartographique par défaut sur votre téléphone est plus facile que vous ne le pensez. Suivez les étapes ci-dessous – Étapes préalables – Vous devez avoir Gmail installé sur votre téléphone. Étape 1 – Ouvrez l'AppStore. Étape 2 – Recherchez « Gmail ». Étape 3 – Cliquez à côté de l'application Gmail
 La multiplication matricielle universelle de CUDA : de l'entrée à la maîtrise !
Mar 25, 2024 pm 12:30 PM
La multiplication matricielle universelle de CUDA : de l'entrée à la maîtrise !
Mar 25, 2024 pm 12:30 PM
La multiplication matricielle générale (GEMM) est un élément essentiel de nombreuses applications et algorithmes, et constitue également l'un des indicateurs importants pour évaluer les performances du matériel informatique. Une recherche approfondie et l'optimisation de la mise en œuvre de GEMM peuvent nous aider à mieux comprendre le calcul haute performance et la relation entre les systèmes logiciels et matériels. En informatique, une optimisation efficace de GEMM peut augmenter la vitesse de calcul et économiser des ressources, ce qui est crucial pour améliorer les performances globales d’un système informatique. Une compréhension approfondie du principe de fonctionnement et de la méthode d'optimisation de GEMM nous aidera à mieux utiliser le potentiel du matériel informatique moderne et à fournir des solutions plus efficaces pour diverses tâches informatiques complexes. En optimisant les performances de GEMM
 Comment calculer l'addition, la soustraction, la multiplication et la division dans un document Word
Mar 19, 2024 pm 08:13 PM
Comment calculer l'addition, la soustraction, la multiplication et la division dans un document Word
Mar 19, 2024 pm 08:13 PM
WORD est un traitement de texte puissant. Nous pouvons utiliser Word pour éditer divers textes. Dans les tableaux Excel, nous maîtrisons les méthodes de calcul d'addition, de soustraction et de multiplicateurs. Ainsi, si nous avons besoin de calculer l'addition de valeurs numériques dans les tableaux Word, Comment soustraire le multiplicateur ? Puis-je utiliser uniquement une calculatrice pour le calculer ? La réponse est bien sûr non, WORD peut aussi le faire. Aujourd'hui, je vais vous apprendre à utiliser des formules pour calculer des opérations de base telles que l'addition, la soustraction, la multiplication et la division dans des tableaux dans des documents Word. Apprenons ensemble. Alors, aujourd'hui, permettez-moi de vous montrer en détail comment calculer l'addition, la soustraction, la multiplication et la division dans un document WORD ? Étape 1 : ouvrez un WORD, cliquez sur [Tableau] sous [Insérer] dans la barre d'outils et insérez un tableau dans le menu déroulant.
 Comment écrire un programme de compte à rebours simple en C++ ?
Nov 03, 2023 pm 01:39 PM
Comment écrire un programme de compte à rebours simple en C++ ?
Nov 03, 2023 pm 01:39 PM
C++ est un langage de programmation largement utilisé qui est très pratique pour écrire des programmes de compte à rebours. Le programme de compte à rebours est une application courante qui peut nous fournir des fonctions de calcul du temps et de compte à rebours très précises. Cet article explique comment utiliser C++ pour écrire un programme de compte à rebours simple. La clé pour mettre en œuvre un programme de compte à rebours est d’utiliser une minuterie pour calculer le passage du temps. En C++, nous pouvons utiliser les fonctions du fichier d'en-tête time.h pour implémenter la fonction timer. Ce qui suit est le code d'un simple programme de compte à rebours
 Application d'horloge manquante sur iPhone : comment y remédier
May 03, 2024 pm 09:19 PM
Application d'horloge manquante sur iPhone : comment y remédier
May 03, 2024 pm 09:19 PM
L'application horloge est-elle absente de votre téléphone ? La date et l'heure apparaîtront toujours sur la barre d'état de votre iPhone. Cependant, sans l'application Horloge, vous ne pourrez pas utiliser l'horloge mondiale, le chronomètre, le réveil et bien d'autres fonctionnalités. Par conséquent, réparer l’application d’horloge manquante devrait figurer en haut de votre liste de tâches. Ces solutions peuvent vous aider à résoudre ce problème. Correctif 1 – Placer l’application Horloge Si vous avez supprimé par erreur l’application Horloge de votre écran d’accueil, vous pouvez remettre l’application Horloge à sa place. Étape 1 – Déverrouillez votre iPhone et commencez à faire glisser votre doigt vers la gauche jusqu'à atteindre la page Bibliothèque d'applications. Étape 2 – Ensuite, recherchez « horloge » dans le champ de recherche. Étape 3 – Lorsque vous voyez « Horloge » ci-dessous dans les résultats de recherche, maintenez-la enfoncée et
 Comment ouvrir un site Web à l'aide du Planificateur de tâches
Oct 02, 2023 pm 11:13 PM
Comment ouvrir un site Web à l'aide du Planificateur de tâches
Oct 02, 2023 pm 11:13 PM
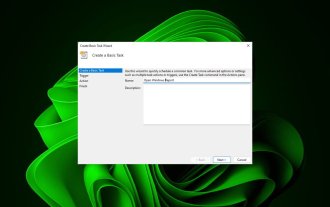
Visitez-vous fréquemment le même site Web à peu près à la même heure chaque jour ? Cela peut conduire à passer beaucoup de temps avec plusieurs onglets de navigateur ouverts et à encombrer le navigateur lors de l'exécution des tâches quotidiennes. Eh bien, que diriez-vous de l’ouvrir sans avoir à lancer le navigateur manuellement ? C'est très simple et ne nécessite pas de télécharger d'applications tierces, comme indiqué ci-dessous. Comment configurer le Planificateur de tâches pour ouvrir un site Web ? Appuyez sur la touche , tapez Planificateur de tâches dans la zone de recherche, puis cliquez sur Ouvrir. Windows Dans la barre latérale droite, cliquez sur l'option Créer une tâche de base. Dans le champ Nom, saisissez le nom du site Web que vous souhaitez ouvrir et cliquez sur Suivant. Ensuite, sous Déclencheurs, cliquez sur Fréquence temporelle, puis sur Suivant. Sélectionnez la durée pendant laquelle vous souhaitez que l'événement se répète et cliquez sur Suivant. Sélectionnez activer
 Comment compter le nombre d'éléments dans une liste à l'aide de la fonction count() de Python
Nov 18, 2023 pm 02:53 PM
Comment compter le nombre d'éléments dans une liste à l'aide de la fonction count() de Python
Nov 18, 2023 pm 02:53 PM
Comment utiliser la fonction count() de Python pour compter le nombre d'éléments dans une liste nécessite des exemples de code spécifiques. En tant que langage de programmation puissant et facile à apprendre, Python fournit de nombreuses fonctions intégrées pour gérer différentes structures de données. L'une d'elles est la fonction count(), qui peut être utilisée pour compter le nombre d'éléments dans une liste. Dans cet article, nous expliquerons en détail comment utiliser la fonction count() et fournirons des exemples de code spécifiques. La fonction count() est une fonction intégrée de Python, utilisée pour calculer un certain
 Impossible d'autoriser l'accès à la caméra et au microphone sur iPhone
Apr 23, 2024 am 11:13 AM
Impossible d'autoriser l'accès à la caméra et au microphone sur iPhone
Apr 23, 2024 am 11:13 AM
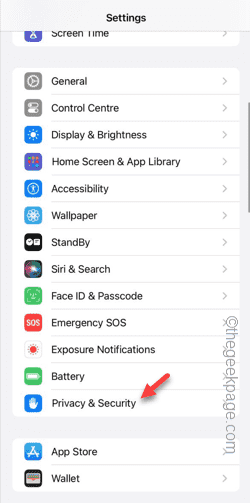
Le message « Impossible d'autoriser l'accès à la caméra et au microphone » s'affiche-t-il lorsque vous essayez d'utiliser l'application ? En règle générale, vous accordez des autorisations de caméra et de microphone à des personnes spécifiques en fonction de leurs besoins. Cependant, si vous refusez l'autorisation, la caméra et le microphone ne fonctionneront pas et afficheront ce message d'erreur à la place. Résoudre ce problème est très simple et vous pouvez le faire en une minute ou deux. Correctif 1 – Fournir les autorisations de caméra et de microphone Vous pouvez fournir les autorisations de caméra et de microphone nécessaires directement dans les paramètres. Étape 1 – Accédez à l'onglet Paramètres. Étape 2 – Ouvrez le panneau Confidentialité et sécurité. Étape 3 – Activez-y l’autorisation « Caméra ». Étape 4 – À l’intérieur, vous trouverez une liste des applications qui ont demandé l’autorisation d’accéder à l’appareil photo de votre téléphone. Étape 5 – Ouvrez la « Appareil photo » de l'application spécifiée






