 développement back-end
développement back-end
 C++
C++
 Quelle est l'aire d'un cercle à l'intérieur d'un rectangle inscrit dans un demi-cercle ?
Quelle est l'aire d'un cercle à l'intérieur d'un rectangle inscrit dans un demi-cercle ?
Quelle est l'aire d'un cercle à l'intérieur d'un rectangle inscrit dans un demi-cercle ?
Un cercle inscrit dans un rectangle est tangent au côté le plus long du rectangle, c'est-à-dire que la longueur est tangente au cercle.
Un rectangle inscrit dans un demi-cercle touche deux points sur l'arc du demi-cercle. La largeur du rectangle est égale au diamètre du cercle.
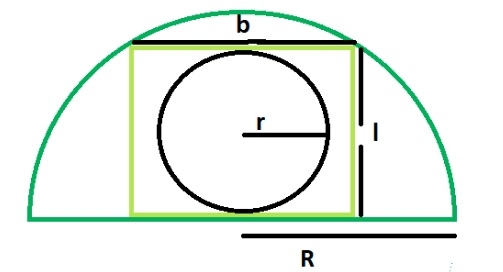
Si R est le rayon du demi-cercle.
La longueur du rectangle = √2R/2
La largeur du rectangle = R/√2
Le rayon du cercle inscrit est
r = b/2 = R/2 √2
En utilisant cette formule on peut calculer l'aire d'un cercle inscrit dans un rectangle inscrit dans un demi-cercle,
Aire = (π*r2) = π*R/8
Exemple
Démo
#include <stdio.h>
int main() {
float a = 5;
float area = 3.14 * a/ 8;
printf("The area of the circle inscribed in a rectangle inscribed in a semicircle of radius %f is %f", a , area);
return 0;
}Sortie
The area of the circle inscribed in a rectangle inscribed in a semicircle of radius 5.00000 is 1.962500
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Quelle est l'aire d'un cercle inscrit dans un losange ?
Sep 05, 2023 am 08:25 AM
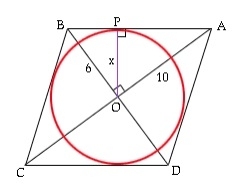
Quelle est l'aire d'un cercle inscrit dans un losange ?
Sep 05, 2023 am 08:25 AM
Le cercle inscrit d'un losange est tangent à ses quatre côtés et à ses quatre extrémités. Les côtés d'un losange sont tangents au cercle. Ici, r est le rayon trouvé en utilisant a et la diagonale de la valeur donnée. Maintenant, le triangle d'aire AOB = ½*OA*OB = ½*AB*r (tous deux utilisant la formule ½*b*h). ½*a/2*b/2=½*(√(a2/4+b2/4))*ra*b/8=√(a2+b2)*r/4r=a*b/2√(a2 +b2) Aire du cercle = π*r*r=π*(a2*b2)/4(a2support>+b2) Exemple des diagonales des losanges 5 et 10. La zone est 15,700000 Exemple de code Démonstration en temps réel #include<stdio.h>intma
 Comment marquer la zone en CAO
Mar 14, 2023 am 11:30 AM
Comment marquer la zone en CAO
Mar 14, 2023 am 11:30 AM
Méthode d'étiquetage des zones en CAO : 1. Ouvrez CAD, cliquez sur "Dessiner" pour dessiner des graphiques ; 2. Entrez la commande "ZONE" et appuyez sur Entrée ; 3. Sélectionnez la zone ; 4. Appuyez sur la barre d'espace pour afficher la zone de la zone ; 5. Entrez la commande "T" puis entrez la taille de la zone à l'intérieur de la zone.
 Quelle est l'aire d'un cercle à l'intérieur d'un rectangle inscrit dans un demi-cercle ?
Sep 13, 2023 am 08:45 AM
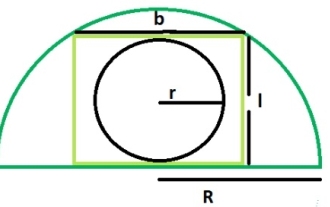
Quelle est l'aire d'un cercle à l'intérieur d'un rectangle inscrit dans un demi-cercle ?
Sep 13, 2023 am 08:45 AM
Un cercle inscrit dans un rectangle est tangent au côté le plus long du rectangle, c'est-à-dire que sa longueur est tangente au cercle. Un rectangle inscrit dans un demi-cercle touche deux points sur l'arc du demi-cercle. La largeur du rectangle est égale au diamètre du cercle. Si R est le rayon du demi-cercle. La longueur du rectangle = √2R/2 La largeur du rectangle = R/√2 Le rayon du cercle inscrit est r = b/2 = R/2√2 En utilisant cette formule on peut calculer le rectangle inscrit dans le demi-cercle L'aire d'un cercle, aire = (π*r2)=π*R/8 Exemple de démonstration #include<stdio.h>intmain(){&
 Quelle est la superficie du secteur circulaire ?
Aug 30, 2023 am 08:33 AM
Quelle est la superficie du secteur circulaire ?
Aug 30, 2023 am 08:33 AM
Un secteur circulaire, également appelé secteur circulaire/secteur de cercle, est une portion de cercle délimitée par un arc entre deux rayons. Cette zone est délimitée par deux rayons et un arc. Pour trouver la zone inscrite, nous devons trouver l’angle entre les deux rayons. La superficie totale est égale à 360 degrés d'angle. Pour trouver l’aire d’un angle, on multiplie l’aire par θ/360. Cela donne l'aire de la partie inscrite. où θ est l'angle entre les deux rayons (en degrés). L'aire du secteur circulaire = π*r*r*(θ/360). Par exemple, l'aire d'un secteur circulaire d'un rayon de 5 et d'un angle de 60 degrés est de 13,083. Zone=(3,14*5*5)*(60/360)=13,03Exemple de codeDémo#incl
 Comment fusionner un graphique après la dispersion des rectangles CAO
Feb 28, 2024 pm 12:10 PM
Comment fusionner un graphique après la dispersion des rectangles CAO
Feb 28, 2024 pm 12:10 PM
Lorsque nous utilisons un logiciel de CAO, nous rencontrons souvent des situations dans lesquelles nous devons recombiner des objets rectangulaires « dispersés » en un seul graphique. Ce besoin se fait sentir dans de nombreux domaines, comme l’aménagement de l’espace, la conception mécanique et les dessins architecturaux. Afin de répondre à cette demande, nous devons comprendre et maîtriser certaines fonctions clés des logiciels de CAO. Ensuite, l'éditeur de ce site vous présentera en détail comment réaliser cette tâche dans l'environnement CAO. Les utilisateurs qui ont des doutes peuvent venir suivre cet article pour apprendre. Méthode pour fusionner des rectangles CAO en un seul graphique après les avoir divisés : 1. Ouvrez le logiciel CAD2023, créez un rectangle, puis entrez la commande X et un espace. Comme indiqué ci-dessous : 2. Sélectionnez l'objet rectangulaire et espacez-le. Vous pouvez briser les objets. 3. Sélectionnez toutes les lignes ouvertes
 Comment mesurer la zone des graphiques dans CAD Viewer. Comment mesurer la zone des graphiques dans CAD Viewer.
Mar 13, 2024 pm 01:43 PM
Comment mesurer la zone des graphiques dans CAD Viewer. Comment mesurer la zone des graphiques dans CAD Viewer.
Mar 13, 2024 pm 01:43 PM
Comment mesurer la surface d'un graphique dans CAD Viewer ? CAD Viewer est un logiciel très simple à utiliser pour visualiser des dessins techniques. Ce logiciel a de nombreuses fonctions et des dessins dans différents formats peuvent être ouverts et visualisés. Si, lorsque nous regardons les dessins, nous constatons que la mesure de la surface de certains graphiques est erronée ou que certains graphiques oublient de mesurer la surface, nous pouvons utiliser ce logiciel pour mesurer la surface des graphiques. Alors, comment mesurer la surface des graphiques ? Ci-dessous, l'éditeur de ce site a compilé les étapes du roi du dessin CAO pour mesurer la surface des graphiques pour votre référence. Étapes pour mesurer la zone graphique dans CAD Viewer 1. Tout d'abord, ouvrez le fichier de dessin dans l'application CAD Viewer, prenez le dessin avec des graphiques en arc comme exemple et mesurez la zone du graphique. 2. Après avoir ouvert le dessin, allez en bas de l'interface du logiciel
 Écrire un programme Java pour calculer l'aire et le périmètre d'un rectangle en utilisant le concept de classes
Sep 03, 2023 am 11:37 AM
Écrire un programme Java pour calculer l'aire et le périmètre d'un rectangle en utilisant le concept de classes
Sep 03, 2023 am 11:37 AM
Le langage Java est aujourd’hui l’un des langages de programmation orientés objet les plus utilisés dans le monde. Le concept de classes est l’une des caractéristiques les plus importantes des langages orientés objet. Une classe est comme un modèle pour un objet. Par exemple, lorsque nous voulons construire une maison, nous créons d’abord un plan de la maison, en d’autres termes, nous créons un plan qui montre comment nous allons construire la maison. Selon ce plan, nous pouvons construire de nombreuses maisons. De même, en utilisant des classes, nous pouvons créer de nombreux objets. Les classes sont des plans pour créer de nombreux objets, où les objets sont des entités du monde réel telles que des voitures, des vélos, des stylos, etc. Une classe possède les caractéristiques de tous les objets, et les objets ont les valeurs de ces caractéristiques. Dans cet article, nous allons écrire un programme Java pour trouver le périmètre et les faces d'un rectangle en utilisant le concept de classes
 Trouver l'aire d'un cercle inscrit dans un carré en Java
Aug 19, 2023 pm 04:53 PM
Trouver l'aire d'un cercle inscrit dans un carré en Java
Aug 19, 2023 pm 04:53 PM
Un cercle est autour d'un diagramme bidimensionnel en forme qui n'a pas de coins. Chaque cercle a un point d'origine et chaque point du cercle maintient une distance égale par rapport à l'origine. La distance entre l'origine et le point dans un cercle est connue sous le nom de rayon du cercle. Et de même, si nous traçons une ligne à partir de





