 développement back-end
développement back-end
 C++
C++
 Quelle est la traduction en C du plus grand triangle de la Ruhr dans un carré inscrit dans un cercle ?
Quelle est la traduction en C du plus grand triangle de la Ruhr dans un carré inscrit dans un cercle ?
Quelle est la traduction en C du plus grand triangle de la Ruhr dans un carré inscrit dans un cercle ?
Le Triangle de Reuleaux est une forme formée par l'intersection de trois disques, le centre de chaque disque étant situé à la limite des deux autres disques. Sa limite est une courbe de largeur constante, qui est la courbe la plus simple et la plus connue après le cercle lui-même. Une largeur constante signifie que deux lignes de support parallèles sont également espacées, quelle que soit leur orientation. Parce que son diamètre est le même.
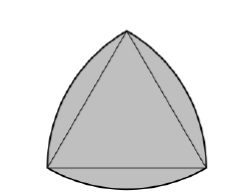
Les limites du triangle de Reuleaux sont des courbes d'égale largeur basées sur le triangle équilatéral. Tous les points d'un côté sont équidistants du sommet opposé.
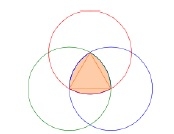
Construction d'un triangle de Reulo
Formule du triangle de Reulo
L'aire d'un triangle de Reulo, si la courbe est basée sur un triangle équilatéral et que le triangle latéral est h
A = (π * h<sup>2</sup>) / 2 – 2 * (Area of equilateral triangle) = (π – √3) * h<sup>2</sup> / 2 = 0.70477 * h<sup>2</sup>
Le plus grand triangle de Reulo dans le carré, inscrit dans le cercle
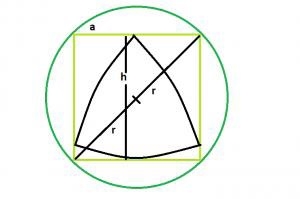
Figure 1. Le plus grand triangle de Reuleaux à l'intérieur du carré, inscrit dans le cercle
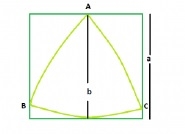
Le plus grand triangle de Reuleaux à l'intérieur du carré
L'aire du triangle de Reuleaux est 0,70477 * b2 où b est la distance entre les droites parallèles supportant le triangle de Reuleaux.
La distance entre les droites parallèles supportant le triangle de Reuleaux = les côtés du carré, soit a
L'aire du triangle de Reuleaux, A = 0,70477 * a2
Donnons un exemple pour l'améliorer Pour illustrer ce concept,
Input: r = 6 Output: 50.7434
montre que le côté du carré
est a, alors
a√2 = 2r
a = √2r
Dans le triangle de Reulo , h = a = √2r,
L'aire du triangle de Reuleaux est, A = 0,70477*h^2 = 0,70477*2*r^2
Exemple
#include <stdio.h>
#include<math.h>
int main() {
float r = 6;
float area = 0.70477 * 2 * pow(r, 2);
printf("The area is : %f",area);
return 0;
}Sortie
The area is : 50.743439
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
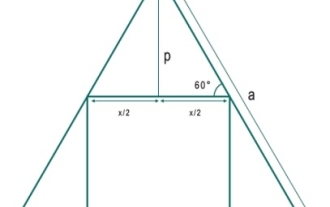 Quel est le plus grand carré pouvant être inscrit dans un triangle équilatéral ?
Sep 22, 2023 pm 06:21 PM
Quel est le plus grand carré pouvant être inscrit dans un triangle équilatéral ?
Sep 22, 2023 pm 06:21 PM
Nous verrons ici l'aire du plus grand carré pouvant être inscrit dans un triangle équilatéral. La longueur du côté du triangle est « a » et la longueur du côté du carré est x. La longueur du côté 'a' du triangle est − donc x est − Exemple #include<iostream>#include<cmath>usingnamespacestd;floatareaSquare(floata){//aissideoftriangle if(a<0)//ifaisnegative,thenthisisi
 Trouver l'aire d'un cercle inscrit dans un carré en Java
Aug 19, 2023 pm 04:53 PM
Trouver l'aire d'un cercle inscrit dans un carré en Java
Aug 19, 2023 pm 04:53 PM
Un cercle est autour d'un diagramme bidimensionnel en forme qui n'a pas de coins. Chaque cercle a un point d'origine et chaque point du cercle maintient une distance égale par rapport à l'origine. La distance entre l'origine et le point dans un cercle est connue sous le nom de rayon du cercle. Et de même, si nous traçons une ligne à partir de
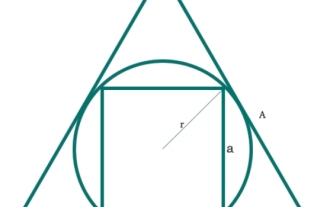 Dans un programme C, traduisez en chinois : Quelle est l'aire d'un carré inscrit dans un cercle inscrit dans un triangle équilatéral ?
Aug 31, 2023 pm 12:25 PM
Dans un programme C, traduisez en chinois : Quelle est l'aire d'un carré inscrit dans un cercle inscrit dans un triangle équilatéral ?
Aug 31, 2023 pm 12:25 PM
Nous verrons ici que l'aire d'un carré est inscrite dans un cercle, et que le cercle est inscrit dans un triangle équilatéral. Le côté du carré est "a". Le rayon du cercle est "r" et le côté de l'hexagone est "A". Le graphique est présenté ci-dessous. Donc la diagonale du carré est - donc l'aire du carré est - Exemple #include<iostream>#include<cmath>usingnamespacestd;floatarea(floatA){//Aisthesideofthetriangle if(A<0)//ifthevalueisne
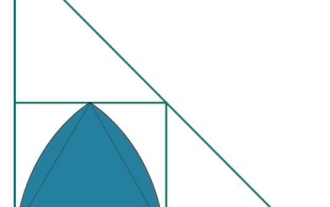 Quel est le plus grand triangle de Ruero inscrit dans un carré qui est un triangle rectangle ?
Sep 04, 2023 pm 10:29 PM
Quel est le plus grand triangle de Ruero inscrit dans un carré qui est un triangle rectangle ?
Sep 04, 2023 pm 10:29 PM
Ici, nous verrons l'aire du plus grand triangle de Reuleaux inscrite dans un carré, qui à son tour est inscrit dans un triangle rectangle. La longueur du côté du carré est « a ». La hauteur d'un triangle de Reuleaux est x. La base du triangle est b, la hauteur est l et l'hypoténuse est h. Nous savons qu'un carré inscrit dans un triangle rectangle de hauteur l et de base b a une longueur de côté - la hauteur d'un triangle de Reuleaux est la même que a. Donc a=x. Par conséquent, l'aire d'un triangle de Reuleaux est - Exemple#include<iostream>#include<cmath>usingnamespacestd;fl
 Programme C pour calculer l'aire d'un carré dans un cercle inscrit dans un hexagone
Aug 28, 2023 pm 08:41 PM
Programme C pour calculer l'aire d'un carré dans un cercle inscrit dans un hexagone
Aug 28, 2023 pm 08:41 PM
Étant donné un carré inscrit dans un cercle inscrit par un hexagone régulier, nous devons trouver l'aire du carré, et pour ce faire, nous devons trouver la relation entre les longueurs des côtés du carré et les longueurs des côtés de l'hexagone régulier . La formule mathématique du rayon du cercle inscrit d'un hexagone régulier est : r=A√3/2 Puisque la diagonale du carré est égale au diamètre du cercle, la relation entre le rayon et la longueur du côté est : a=√r Selon l'hexagone régulier Longueur du côté de, a=√3A/√2, Donc l'aire du carré, Area=a2=(√3A/√2)2 Exemple #include<stdio. h>#inclu
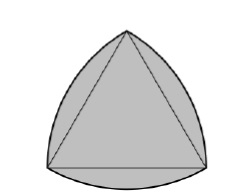 En C, le plus grand triangle de Reuleaux à l'intérieur d'un carré
Sep 07, 2023 pm 12:29 PM
En C, le plus grand triangle de Reuleaux à l'intérieur d'un carré
Sep 07, 2023 pm 12:29 PM
Un triangle de Lule est une forme formée par l'intersection de trois disques, le centre de chaque disque étant à la limite des deux autres disques. Sa limite est une courbe de largeur constante et, mis à part le cercle lui-même, c'est la courbe de ce type la plus simple et la plus connue. Une largeur constante signifie que l'espacement entre chacune des deux lignes de support parallèles est le même, quelle que soit leur orientation. Parce que tous ses diamètres sont les mêmes. Les limites d'un triangle de Lule sont des courbes de largeur constante basées sur des triangles équilatéraux. Tous les points d'une arête sont équidistants du sommet opposé. La formule pour construire un triangle de Lule Si la courbe est basée sur un triangle équilatéral et que la longueur du côté du triangle est h, alors l'aire du triangle de Lule est A=(π*h2)/2–2*( Zoneo
 Quelle est l'aire d'une feuille dans un carré ?
Aug 26, 2023 pm 05:13 PM
Quelle est l'aire d'une feuille dans un carré ?
Aug 26, 2023 pm 05:13 PM
Ici, nous verrons comment calculer l'aire d'un objet en forme de feuille qui se trouve dans un carré ABCD. Chaque côté du carré a une longueur « a ». La feuille comporte deux parties égales. L'aire de chaque partie est p, maintenant − l'aire de la feuille entière est 2p. Exemple #include<iostream>usingnamespacestd;floatleafArea(floata){ return(a*a*(3.1415/2-1));}intmain(){ floatsquare
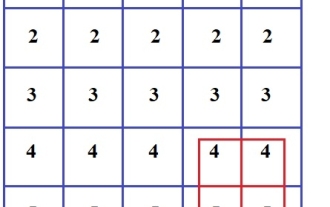 Imprimer la sous-matrice carrée de somme maximale d'une taille donnée dans le programme C
Sep 07, 2023 pm 01:53 PM
Imprimer la sous-matrice carrée de somme maximale d'une taille donnée dans le programme C
Sep 07, 2023 pm 01:53 PM
Étant donné une matrice NxN, trouver une sous-matrice MxM avec M=1 telle que la somme de tous les éléments de la matrice MxM soit maximale. L'entrée de la matrice NxN peut contenir des valeurs entières nulles, positives et négatives. Exemple d'entrée : {{1,1,1,1,1}, {2,2,2,2,2}, {3,3,3,3,3}, {4,4,4,4,4 }, {5,5,5,5,5}}Sortie :&





