Programme Python pour obtenir l'élément central d'une liste chaînée, complété en une seule itération

Les listes chaînées sont utilisées pour stocker des données dans des emplacements mémoire non contigus. Les nœuds contenant des éléments de données sont liés à l'aide de pointeurs. Chaque nœud se compose de deux champs. Le premier champ est utilisé pour stocker les données et le deuxième champ contient le lien vers le nœud suivant.

Technologie de fissuration par force brute

Pour trouver l'élément central d'une liste chaînée, la technique de la force brute consiste à trouver la longueur de la liste chaînée en parcourant toute la liste chaînée jusqu'à ce que NULL soit rencontré, puis en divisant la longueur par 2 pour obtenir l'élément central de la liste chaînée. l'index de la liste. Après avoir obtenu l'index de l'élément intermédiaire, parcourez à nouveau la liste chaînée depuis le début et arrêtez-vous lorsque l'index requis est atteint. La donnée à cet index donne l'élément intermédiaire.

• Prenez une variable nommée "temp" pointant vers HEAD et initialisez "len" à 0

• Utilisez temp pour parcourir la liste chaînée jusqu'à ce que NULL soit atteint, et incrémentez "len" de 1 à chaque nœud.

• Après avoir obtenu la longueur de la liste chaînée, initialisez à nouveau temp sur HEAD. Parcourez la liste chaînée jusqu'à len//2.

Utilisez des pointeurs lents et rapides (itération unique)

Nous utiliserons deux pointeurs pour parcourir la liste chaînée. L’un est appelé « pointeur lent » et l’autre « pointeur rapide ».

Le pointeur rapide se déplace deux fois plus vite que le pointeur lent.

Lorsque le pointeur rapide atteint la fin de la liste chaînée, le pointeur lent sera au nœud du milieu.

Par conséquent, nous pouvons imprimer directement le contenu des nœuds intermédiaires.

Exemple

Considérez la liste de liens ci-dessous. L'élément du milieu est 3.

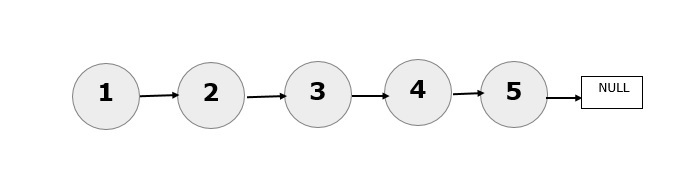
Le pointeur rapide a atteint le dernier nœud de la liste chaînée et le pointeur lent pointe désormais vers le nœud 3. Par conséquent, 3 est l’élément central de la liste chaînée donnée. Considérons maintenant 6 nœuds.

Exemple

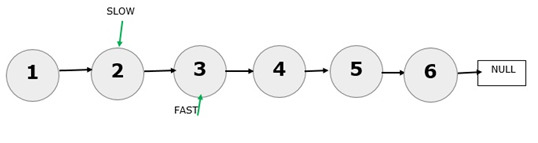
Le pointeur rapide a atteint NULL et le pointeur lent pointe vers le 4ème nœud. L’élément du milieu est donc 4.

Algorithme

• Faites pointer "lent" et "rapide" vers la TÊTE de la liste chaînée.

• Augmentez le pointeur rapide de 2 et le pointeur lent de 1 jusqu'à ce que le pointeur rapide et fast.next ne soient pas égaux à NULL

• Imprimez la valeur au niveau du pointeur lent.

• La complexité temporelle est O(n).

class Node:
  def __init__(self, val):
      self.val = val
      self.next = None
class LinkedList:
  def __init__(self):
      self.head = None

  def insert_at_the_beginning(self, newVal):
      newNode = Node(newVal)
      newNode.next = self.head
      self.head = newNode
  def print_middle_element(self):
      slow=self.head
      fast=self.head
      while fast is not None and fast.next is not None:
          slow=slow.next      #slow pointer moves one node
          fast=fast.next.next  #fast pointer moves two nodes
      print("\n\nthe middle element is ",slow.val)
  def Print_the_LL(self):
      temp = self.head
      if(temp != None):
        print("The linked list elements are:", end=" ")
        while (temp != None):
          print(temp.val, end=" ")
          temp = temp.next
      else:
        print("The list is empty.")
newList = LinkedList()
newList.insert_at_the_beginning(5)
newList.insert_at_the_beginning(4)
newList.insert_at_the_beginning(3)
newList.insert_at_the_beginning(2)
newList.insert_at_the_beginning(1)
newList.Print_the_LL()
newList.print_middle_element()

Sortie

The linked list elements are: 1 2 3 4 5 

the middle element is  3

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!