
Pour ceux qui sont dans le domaine de la recherche scientifique, vous avez plus ou moins entendu parler du problème P/NP. Ce problème a été inclus dans les problèmes du Prix du Millénaire par le Clay Institute of Mathematics. Il comporte sept problèmes majeurs. La conjecture bien connue de Poincaré, l'hypothèse de Riemann, etc. sont incluses. Et l’organisation a offert des millions de dollars en prix aux chercheurs qui parviendront à résoudre le problème.
Le problème P/NP a été proposé pour la première fois en 1971 respectivement par Stephen A. Cook et Leonid Levin. Au fil des années, de nombreuses personnes se sont consacrées à la recherche sur ce problème. Cependant, certaines personnes disent qu'il faudra peut-être une estimation prudente de 100 ans pour résoudre le problème P=NP
Ces dernières années, certaines personnes ont prétendu avoir prouvé que P est égal ou non à NP, mais là Il y a des erreurs dans ces processus de preuve. Cependant, jusqu'à présent, personne n'a été en mesure de donner une réponse définitive
Avec le développement de la technologie de l'intelligence artificielle, en particulier la mise à jour rapide des grands modèles de langage au cours de l'année écoulée, les chercheurs ont commencé à essayer d'utiliser la technologie de l'intelligence artificielle pour résoudre certains problèmes mondiaux
Des chercheurs de Microsoft Research, de l'Université de Pékin, de l'Université de Beihang et d'autres institutions ont proposé d'utiliser de grands modèles de langage (LLM) pour améliorer et accélérer la recherche sur les problèmes P versus NP
Cet article propose A Un cadre commun, le raisonnement socratique, est utilisé pour inciter le LLM à réfléchir profondément et à résoudre des problèmes complexes. Sur la base de ce cadre, LLM est capable de découvrir, résoudre et intégrer de manière récursive des problèmes, tout en effectuant également une auto-évaluation et une amélioration.
L'étude pilote de cet article sur le problème P vs. NP montre que GPT-4 génère avec succès un Prouvez le modèle et menez un raisonnement rigoureux au cours de 97 cycles de dialogue, pour arriver à la conclusion que « P≠ NP », ce qui est cohérent avec la conclusion de (Xu et Zhou, 2023).

Veuillez cliquer sur le lien suivant pour consulter l'article : https://arxiv.org/pdf/2309.05689.pdf
La principale contribution de cet article peut être résumée comme suit :
Contenu réécrit : ce paragraphe mentionne qu'ils ont nommé le cadre "Raisonnement socratique" après avoir été inspiré par l'ancien philosophe grec Socrate. Socrate a dit un jour : "Je ne peux rien enseigner à personne. Je peux seulement les faire réfléchir." Et l'idée globale de conception du cadre est la même. Il s'agit d'un cadre général de résolution de problèmes qui permet d'utiliser le LLM. un large éventail de Naviguez dans l'espace des solutions et obtenez des réponses efficacement
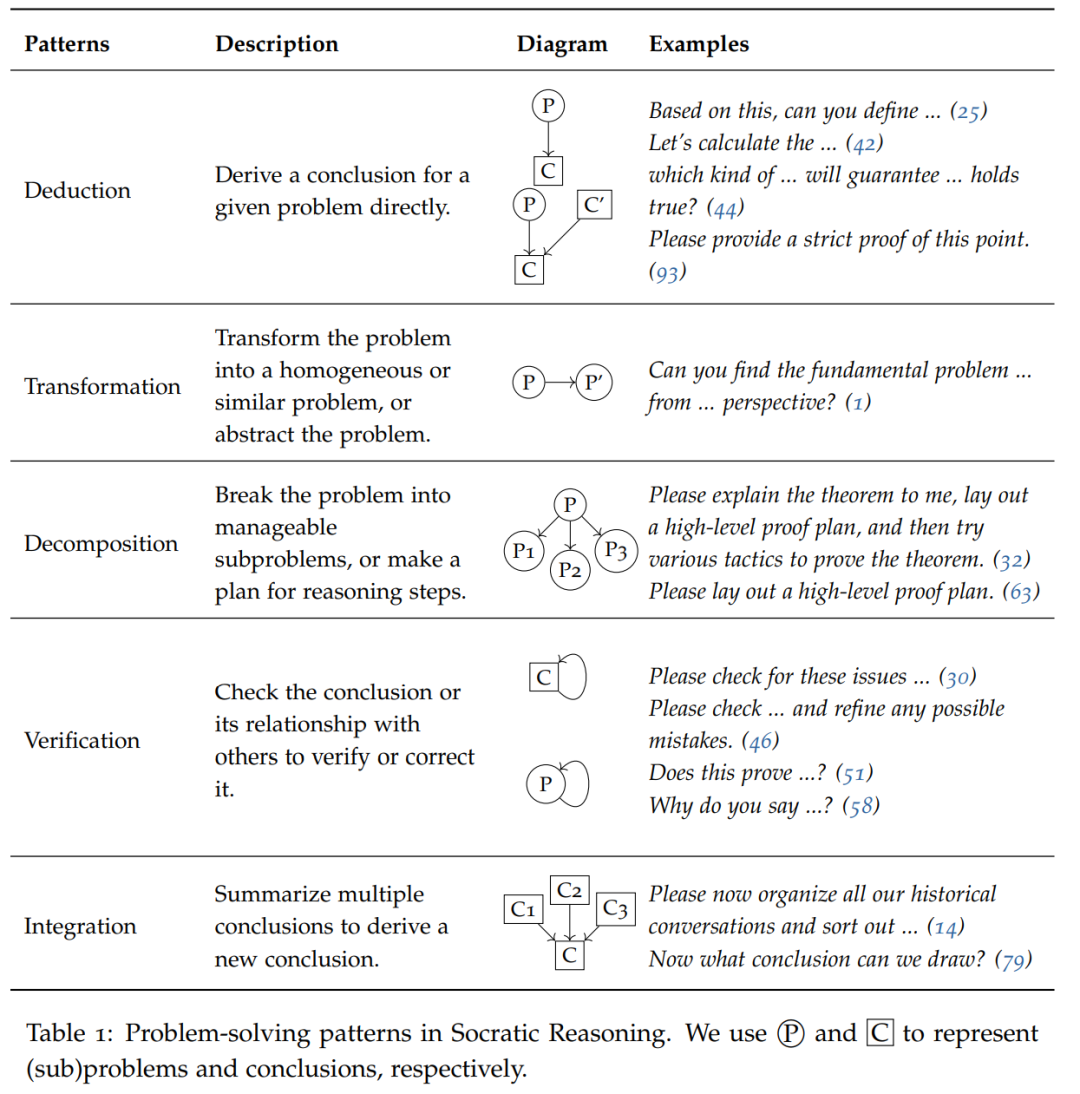
Le tableau 1 répertorie les cinq modes d'invite du « raisonnement socratique » : déduction, transformation, décomposition, vérification et fusion. Ces modèles sont utilisés pour découvrir de nouvelles idées et perspectives, décomposer des problèmes complexes en sous-problèmes ou petites étapes, et s'améliorer en remettant en question et en répondant aux réponses
Sur des problèmes plus petits (problèmes atomiques), le LLM peut directement Compte tenu des résultats du raisonnement , le mode déductif est utilisé (par exemple, l'invite est « Réfléchissons étape par étape... ») pour guider LLM afin de tirer directement des conclusions.
Pour des problèmes plus complexes, cet article demande d'abord au LLM de transformer le problème en un nouveau problème ou de le décomposer en plusieurs sous-problèmes. Ces modèles sont ensuite exécutés de manière récursive jusqu'à ce que le problème du ji atomique soit atteint.
Lorsque de nouveaux problèmes surviennent ou que de nouvelles conclusions sont tirées, le mode de vérification doit être adopté et les capacités d'auto-évaluation de LLM doivent être utilisées pour la vérification et l'amélioration
Enfin, le mode fusion nécessite que le LLM synthétise les conclusions basées sur les résultats des sous-problèmes
Motiver récursivement le LLM à travers une série de conversations pour continuer le processus ci-dessus jusqu'à ce que le problème cible soit résolu
Dans cet ouvrage, "Sucra "Socratic Reasoning" fournit un cadre d'invite systématique pour les problèmes difficiles
L'image ci-dessous est un exemple de dialogue utilisé pour résoudre les problèmes P vs. NP dans "Socratic Reasoning". L'API GPT-4 est utilisée dans l'étude de cas et l'article trie les processus en fonction de l'index rond.

Au cours du processus d'exploration, cet article présente cinq rôles différents en tant que prouveurs auxiliaires, tels que les mathématiciens maîtrisant la théorie des probabilités. L'expérience a mené un total de 97 tours de dialogue, divisés en 14 tours avant et 83 tours après
Par exemple, l'invite du premier tour : Vous pouvez trouver P!=NP d'un point de vue philosophique plutôt que d'une théorie informatique. perspective. Le problème sous-jacent ?示 Voici d'autres conseils :

Le dialogue est en constante évolution, et le dernier tour de dialogue est le suivant : Enfin, conclusion P 

NP

est intéressé. Les lecteurs peuvent consulter l'article original pour en savoir plus.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 À quelle marque appartient le téléphone mobile OnePlus ?
À quelle marque appartient le téléphone mobile OnePlus ?
 La différence entre front-end et back-end
La différence entre front-end et back-end
 Comment résoudre le problème selon lequel WLAN n'a pas de configuration IP valide
Comment résoudre le problème selon lequel WLAN n'a pas de configuration IP valide
 Dernier prix d'ondulation
Dernier prix d'ondulation
 Utilisation de la fonction isalpha
Utilisation de la fonction isalpha
 Comment écrire un triangle en CSS
Comment écrire un triangle en CSS
 fonction de balise span
fonction de balise span
 méthode de pagination mysql
méthode de pagination mysql