Utilisez l'addition ou la soustraction pour obtenir le nombre minimum d'étapes pour N à chaque étape

À partir de l'énoncé du problème ci-dessus, notre tâche est d'obtenir le nombre minimum d'étapes dans chacune desquelles nous pouvons obtenir le nombre N donné en utilisant l'addition ou la soustraction. Nous pouvons comprendre que nous devons imprimer le nombre minimum d'étapes pouvant être effectuées et l'ordre des étapes pour tout entier N donné, en ajoutant et en soustrayant les numéros d'étape pour arriver à un nombre commençant à 0.

Dans cet ensemble de problèmes, nous pouvons ajouter ou soustraire un nombre égal au nombre d'étapes jusqu'à la position actuelle à chaque étape. Par exemple, nous pouvons ajouter 1 ou -1 à l'étape 1. De plus, nous pouvons ajouter 2 ou -2 à l'étape 2 et ainsi de suite. Nous pouvons ajouter ou soustraire des nombres à chaque étape en fonction de la situation.

Le principal défi de ce problème est que nous devons effectuer le nombre minimum d'étapes en partant de 0 pour atteindre N. Comprenons mieux ce problème avec un exemple.

L'exemple ci-dessous vous montrera tous les nombres que nous pouvons obtenir en 2 étapes à partir de 0 en effectuant les opérations ci-dessus.

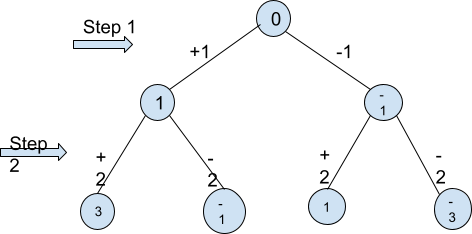
Par exemple, supposons que nous ayons N=1.

Sortie

Minimum no of steps: 1
Sequence of steps: 1

Instructions

Nous pouvons atteindre 1 de deux manières -

• Ajoutez simplement 1 à l'étape 1 pour passer de 0 à 1, ce qui prend 1 étape.

• Soustrayez 1 à l'étape 1 pour passer de 0 à -1, puis ajoutez 2 à l'étape 2 pour passer de -1 à 1, ce qui prend 2 étapes.

Puisque la question indique que nous avons besoin du nombre minimum d'étapes pour atteindre n'importe quel nombre N, la sortie souhaitée pour cette entrée sera 1.

Pour, N=3

Sortie

Minimum no of steps: 2
Sequence of steps: 1 2

Instructions

On ajoute 1 à l'étape 1 pour passer de 0 à 1, puis on ajoute 2 à l'étape 2 pour passer de 1 à 3.

Méthode

La meilleure façon de résoudre le problème est d’abord de déterminer si N est positif ou négatif. Nous devons respectivement ajouter ou soustraire le nombre approprié d’étapes pour résoudre le problème.

• Si N est un nombre positif, continuez à ajouter des étapes jusqu'à ce que la somme soit supérieure ou égale à N.

• De même, si N est négatif, continuez à soustraire le nombre de pas jusqu'à ce que la somme soit supérieure ou égale à N.

• Si la somme est égale à N dans le cas ci-dessus, renvoie le nombre d'étapes et l'ordre des étapes. Le principal problème est de gérer la situation lorsque N est dépassé.

Une fois que la somme dépasse N, vérifiez si (somme-N) est paire ou impaire.

• Si (somme-N) est paire, alors nous devons effectuer une soustraction par étapes de (somme-N)/2 pour atteindre N.

  Comprenons mieux ce cas avec un exemple approprié.

  Pour, N=8

  1+2+3+4=10, ce qui est supérieur à 8.

  Parce que 10-8=2 est un nombre pair. Nous allons donc soustraire par pas de 2/2, soit

  Étape 1. L'ordre des étapes sera donc -1 2 3 4 et le minimum

  Le nombre d'étapes pour atteindre N sera de 4.

• Si (somme-N) est un nombre impair, déterminez d'abord si le nombre dont la somme dépasse N à l'étape précédente est pair ou impair.

  Si l'étape précédente était impaire, effectuez une étape en ajoutant le numéro de l'étape suivante qui rendra notre (somme-N) paire, puis effectuez les étapes ci-dessus pour obtenir le résultat souhaité.

  Par exemple, N=9

  1+2+3+4=10, ce qui est supérieur à 9.

  Parce que 10-9=1, c'est un nombre impair. L'étape suivante est 5, qui est un nombre impair, nous faisons donc simplement une étape et ajoutons 5 à la somme pour obtenir 15, ce qui fait (somme-N)=6. Effectuer la soustraction à l'étape 3 vous donnera la séquence 1 2 -3 4 5, qui est le résultat souhaité.

  Supposons que l'étape précédente soit un nombre pair, dans ce cas, nous devons effectuer deux étapes, ajouter la i-ème étape et soustraire l'étape (i+1) pour obtenir (somme-N) sous forme de nombre pair pour obtenir la séquence d’étapes souhaitée.

  Pour N=5

  1+2+3=6, plus de 5.

  Puisque (somme-N) =1, nous considérerons la dernière étape lorsque su dépasse le nombre N. Puisqu'il s'agit d'un nombre pair, nous effectuerons deux étapes, l'étape 4 et l'étape 5. Notre tâche est de faire (somme-N) quand même, en ajoutant à l'étape 4 et en soustrayant à l'étape 5, nous pouvons faire (somme-N) même si 1 est soustrait de la somme. Puisque (somme-N) est égale à 0, on obtient N. Par conséquent, la séquence est 1 2 3 4 -5.

Exemple

Voici le code C++ de la méthode -

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
void minimumStep(int n){
   vector <int> steps; // for storing the sequence
   int totalSum=0; 
   int temp=0;
   if(n>=0){   // if n is positive then temp will store positive
      temp=1;
   } else {
      temp=-1;  // n is negative then temp will store negative
   }
   n=abs(n);
   int step=0;
   for(step=1;totalSum<n;step++){  // for storing the steps till sum is not greater than n
      steps.push_back(temp*step);
   
      totalSum=totalSum+step;
   }
   if(totalSum>temp*n) {  //when sum greater than n 
      if(step%2==0) {   //when step is even 
         totalSum=totalSum-n; 
         if((totalSum)%2!=0) { // when totalSum-n is odd
            steps.push_back(temp*step);  //store the addition of next step 
            steps.push_back((temp*-1)*(step+1));  // store the subtraction of next step 
            totalSum--;  //make totalSum even
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1; 
		} else {        //when step is odd
         totalSum=totalSum-n;
         if((totalSum)%2!=0)  {  // when totalSum-n is odd 
            steps.push_back(temp*step);   //store the next addition value 
            totalSum+=step; 
            step++;
         }
         int check=(totalSum)/2;
         check--;
         steps[check]=steps[check]*-1;
   
      }
   }
   //print the minimum number of steps taken 
   cout<<"The minimum number of steps : "<<steps.size()<<endl;
   //print the steps is stored in vector
      cout<<"Sequence of steps : ";
   for(int i=0;i<steps.size();i++){
      cout<<steps[i]<<" ";
   }
   
}
int main(){
   int m=17;
   minimumStep(m);
   
   return 0;
}

Sortie

The minimum number of steps : 6
Sequence of steps : 1 -2 3 4 5 6

Complexité temporelle : O(sqrt(N))

Complexité spatiale : O(sqrt(N))

Conclusion

Dans cet article, nous essayons d'expliquer la méthode pour trouver le nombre minimum d'étapes pour atteindre N en ajoutant ou en soustrayant à chaque étape et en imprimant la séquence. J'espère que cet article vous aidera à mieux apprendre ce concept.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!