 développement back-end
développement back-end
 C++
C++
 Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Ici, nous verrons un problème intéressant, nous ajouterons une valeur plus grande à chaque nœud dans un arbre de recherche binaire donné. Ainsi, l'arbre initial et final ressemblera à ceci -
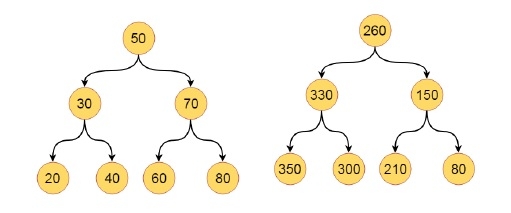
Algorithme
bstUpdate(root, sum) -
Begin if root is null, then stop bstUpdate(right of room, sum) sum := sum + value of root update root value using sum bstUpdate(left of room, sum) End
Example
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node *getNode(int item) {
Node *newNode = new Node();
newNode->data = item;
newNode->left = newNode->right = NULL;
return newNode;
}
void updateBST(Node *root, int *sum) {
if (root == NULL)
return;
updateBST(root->right, sum); //update right sub tree
*sum = *sum + root->data;
root->data = *sum; //update root data
updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
int sum = 0;
updateBST(root, &sum);
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
Node* insert(Node* node, int data) {
if (node == NULL)
return getNode(data);
if (data <= node->data) //go to left
node->left = insert(node->left, data);
else //go to right
node->right = insert(node->right, data);
return node;
}
int main() {
int data[] = {50, 30, 20, 40, 70, 60, 80};
int n = sizeof(data)/sizeof(data[0]);
Node *root = NULL;
for(int i = 0; i < n; i++) {
root = insert(root, data[i]);
}
BSTUpdate(root);
inorder(root);
}output
350 330 300 260 210 150 80
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Code C++ pour inverser les chemins dans un arbre de recherche binaire à l'aide de files d'attente
Sep 14, 2023 pm 07:21 PM
Code C++ pour inverser les chemins dans un arbre de recherche binaire à l'aide de files d'attente
Sep 14, 2023 pm 07:21 PM
Par exemple, étant donné un arbre de recherche binaire, nous devons inverser son chemin à partir d'une clé spécifique. Façons de trouver la solution Dans cette approche, nous allons créer une file d'attente et pousser tous les nœuds jusqu'à ce que nous obtenions le nœud racine. p>Exemple #include<bits/stdc++.h>usingnamespacestd;structnode{ intkey; structnode*left,*right;};structnode*newNode(intitem){&nb
 Comment implémenter un arbre de recherche binaire en Python
Jun 10, 2023 am 08:57 AM
Comment implémenter un arbre de recherche binaire en Python
Jun 10, 2023 am 08:57 AM
Binary Search Tree (BST) est un algorithme de recherche basé sur des arbres binaires. Sa caractéristique est que la valeur dans le sous-arbre gauche de chaque nœud de l'arbre est inférieure à la valeur de ce nœud, tandis que la valeur dans le sous-arbre droit est supérieure à la valeur de ce nœud. Par conséquent, la complexité temporelle des opérations de recherche et d’insertion BST est O(logN). La méthode d'implémentation d'un arbre de recherche binaire en Python est relativement simple, car Python possède deux structures de données intégrées, des listes et des dictionnaires, qui peuvent toutes deux être utilisées pour implémenter des arbres binaires. ici
 Tas binaire et arbre de recherche binaire en C++
Aug 22, 2023 pm 04:10 PM
Tas binaire et arbre de recherche binaire en C++
Aug 22, 2023 pm 04:10 PM
En programmation C++, le tas binaire et l'arbre de recherche binaire sont deux structures de données couramment utilisées. Elles présentent des similitudes, mais elles présentent également des différences. Cet article présentera respectivement les concepts, les opérations de base et les scénarios d'application des tas binaires et des arbres de recherche binaires. 1. Concept du tas binaire 1.1 Le tas binaire est un arbre binaire complet qui satisfait aux deux propriétés suivantes : 1.1.1 Ordre du tas L'ordre du tas signifie que dans un tas binaire, la valeur de chaque nœud n'est pas supérieure (ou inférieure) à la valeur de son nœud parent. Ici, nous prenons le tas maximum comme exemple, c'est-à-dire que la valeur du nœud racine est la plus grande valeur de tout l'arbre, et
 Java utilise la fonction max() de la classe Math pour obtenir le plus grand de deux nombres
Jul 24, 2023 pm 11:17 PM
Java utilise la fonction max() de la classe Math pour obtenir le plus grand de deux nombres
Jul 24, 2023 pm 11:17 PM
Java utilise la fonction max() de la classe Math pour obtenir la plus grande valeur de deux nombres. En programmation Java, nous devons souvent comparer les tailles de deux nombres, puis sélectionner le plus grand nombre pour effectuer certaines opérations. La classe Math en Java fournit de nombreuses fonctions pour les opérations mathématiques, parmi lesquelles la fonction max() peut nous aider à obtenir la plus grande valeur de deux nombres. La fonction Math.max() est définie comme suit : publicstaticintmax(inta,intb) Cette fonction accepte deux entiers
 Comment écrire un algorithme d'arbre de recherche binaire en utilisant C#
Sep 19, 2023 pm 01:03 PM
Comment écrire un algorithme d'arbre de recherche binaire en utilisant C#
Sep 19, 2023 pm 01:03 PM
Comment utiliser C# pour écrire un algorithme d'arbre de recherche binaire nécessite des exemples de code spécifiques. L'arbre de recherche binaire (BinarySearchTree, appelé BST) est une structure de données couramment utilisée qui présente les caractéristiques d'opérations d'insertion, de recherche et de suppression rapides. En C#, nous pouvons utiliser une approche orientée objet pour écrire un algorithme d'arbre de recherche binaire. Tout d’abord, nous devons définir une classe pour un nœud d’arbre de recherche binaire qui contient une valeur et deux pointeurs vers les nœuds enfants gauche et droit. Le code ressemble à ceci : publicclassBST
 Comment implémenter un algorithme d'arbre de recherche binaire à l'aide de Java
Sep 19, 2023 am 08:48 AM
Comment implémenter un algorithme d'arbre de recherche binaire à l'aide de Java
Sep 19, 2023 am 08:48 AM
Comment utiliser Java pour implémenter l'algorithme d'arbre de recherche binaire L'arbre de recherche binaire (BinarySearchTree, BST en abrégé) est une structure de données couramment utilisée qui peut implémenter efficacement des opérations telles que l'insertion, la suppression et la recherche. Cet article explique comment utiliser Java pour implémenter un arbre de recherche binaire et fournit des exemples de code correspondants. 1. Définition de l'arbre de recherche binaire Un arbre de recherche binaire est un arbre ordonné avec les caractéristiques suivantes : Chaque nœud a une valeur clé unique. La valeur clé du sous-arbre gauche est inférieure à la valeur clé du nœud et la valeur clé du sous-arbre droit est supérieure à la valeur clé du nœud.
 Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Sep 16, 2023 pm 08:45 PM
Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Sep 16, 2023 pm 08:45 PM
Ici, nous verrons un problème intéressant, nous ajouterons une valeur plus grande à chaque nœud dans un arbre de recherche binaire donné. Par conséquent, les arbres initial et final ressembleront à ceci - Algorithme bstUpdate(root,sum) -Begin ifrootisnull,thenstop bstUpdate(rightofroom,sum) sum:=sum+valueofroot updaterootvalueus
 Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Sep 07, 2023 pm 12:17 PM
Ajoutez toutes les valeurs plus grandes dans l'arbre de recherche binaire donné à chaque nœud
Sep 07, 2023 pm 12:17 PM
BST ou Binary Search Tree est une forme d'arbre binaire dans lequel tous les nœuds de gauche ont des valeurs inférieures à la valeur du nœud racine et tous les nœuds de droite ont des valeurs supérieures à la valeur du nœud racine. Pour ce problème, nous prendrons un arbre binaire et y ajouterons toutes les valeurs supérieures à la valeur actuelle du nœud. Le problème "ajouter toutes les valeurs plus grandes à chaque nœud d'un BST" est simplifié pour, pour un BST, ajouter toutes les valeurs de nœud supérieures à la valeur de nœud actuelle à cette valeur de nœud. Ajoutez tous les nœuds de valeur plus grande à chaque nœud dans l'énoncé du problème BST : étant donné un arbre de recherche binaire (BST), nous devons ajouter pour chaque nœud la somme de tous les nœuds de valeur plus grande. Entrez 10 /&nb





