 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Écoutez-moi, Transformer est une machine à vecteurs de support
Écoutez-moi, Transformer est une machine à vecteurs de support
Écoutez-moi, Transformer est une machine à vecteurs de support
Transformer est une machine à vecteurs de support (SVM), une nouvelle théorie qui a déclenché des discussions au sein de la communauté universitaire.
Le week-end dernier, un article de l'Université de Pennsylvanie et de l'Université de Californie à Riverside a tenté d'étudier les principes de la structure Transformer basée sur de grands modèles, sa géométrie optimisée dans la couche d'attention et la séparation des jetons d'entrée optimaux de jetons non optimaux. Une équivalence formelle est établie entre les problèmes SVM limités.
L'auteur a déclaré sur hackernews que cette théorie résout le problème du SVM séparant les « bons » jetons des « mauvais » jetons dans chaque séquence d'entrée. En tant que sélecteur de jetons offrant d'excellentes performances, ce SVM est essentiellement différent du SVM traditionnel qui attribue des étiquettes 0-1 à l'entrée.
Cette théorie explique également comment l'attention induit la parcimonie via softmax : les "mauvais" jetons qui tombent du mauvais côté de la limite de décision SVM sont supprimés par la fonction softmax, tandis que les "bons" jetons sont ceux qui se retrouvent avec des non- jeton de probabilité softmax zéro. Il convient également de mentionner que ce SVM dérive des propriétés exponentielles de softmax.
Après le téléchargement de l'article sur arXiv, les gens ont exprimé leurs opinions les uns après les autres. Certaines personnes ont dit : La direction de la recherche sur l'IA est vraiment en spirale, est-ce qu'elle va revenir en arrière ?
Après avoir bouclé la boucle, les machines à vecteurs de support ne sont toujours pas obsolètes.
Depuis la publication de l'article classique « Attention is All You Need », l'architecture Transformer a apporté des progrès révolutionnaires dans le domaine du traitement du langage naturel (NLP). La couche d'attention de Transformer accepte une série de jetons d'entrée X et évalue la corrélation entre les jetons en calculant 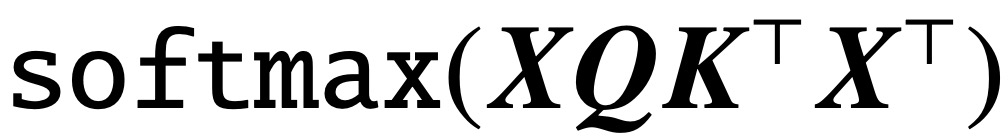 , où (K, Q) sont des paramètres de requête clé pouvant être entraînés, capturant finalement efficacement les dépendances distantes.
, où (K, Q) sont des paramètres de requête clé pouvant être entraînés, capturant finalement efficacement les dépendances distantes.
Maintenant, un nouvel article intitulé "Transformers as Support Vector Machines" établit une équivalence formelle entre la géométrie d'optimisation de l'attention personnelle et le problème SVM à marge dure, en utilisant le produit externe linéaire des paires de jetons. Les contraintes séparent les jetons d'entrée optimaux. à partir de jetons non optimaux.

Lien papier : https://arxiv.org/pdf/2308.16898.pdf
Cette équivalence formelle est basée sur l'article "Max-Margin Token Selection in Attention Mechanism" de Davoud Ataee Tarzanagh et al. "Sur la base de la régularisation Vanishing, convergeant vers une solution SVM qui minimise la norme nucléaire des paramètres combinés
. En revanche, le paramétrage directement via W minimise l'objectif de la norme Frobenius SVM. L'article décrit cette convergence et souligne qu'elle peut se produire dans le sens d'un optimum local plutôt que d'un optimum global. 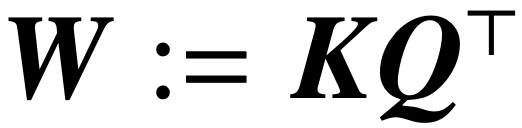 (2) L'article démontre également la convergence directionnelle locale/globale de la descente de gradient de paramétrage W dans des conditions géométriques appropriées. Il est important de noter que la surparamétrage catalyse la convergence globale en garantissant la faisabilité du problème SVM et en garantissant un environnement d'optimisation bénin sans points stationnaires.
(2) L'article démontre également la convergence directionnelle locale/globale de la descente de gradient de paramétrage W dans des conditions géométriques appropriées. Il est important de noter que la surparamétrage catalyse la convergence globale en garantissant la faisabilité du problème SVM et en garantissant un environnement d'optimisation bénin sans points stationnaires.
(3) Bien que la théorie de cette étude s'applique principalement aux têtes de prédiction linéaires, l'équipe de recherche propose un équivalent SVM plus général qui peut prédire la polarisation implicite des transformateurs à 1 couche avec des têtes/MLP non linéaires.
En général, les résultats de cette étude sont applicables aux ensembles de données généraux et peuvent être étendus aux couches d'attention croisée, et la validité pratique des conclusions de l'étude a été vérifiée grâce à des expériences numériques approfondies. Cette étude établit une nouvelle perspective de recherche qui considère les transformateurs multicouches comme des hiérarchies SVM qui séparent et sélectionnent les meilleurs jetons.
Plus précisément, étant donné une séquence d'entrée de longueur T et de dimension d'intégration d
, cette étude analyse les principaux modèles d'attention croisée et d'auto-attention :

où K, Q, V sont respectivement des matrices de clé, de requête et de valeur entraînables, 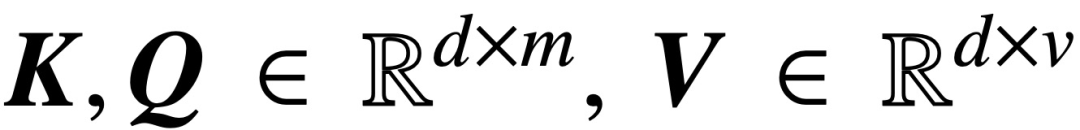 S (・) représente la non-linéarité softmax, qui est appliquée ligne par ligne
S (・) représente la non-linéarité softmax, qui est appliquée ligne par ligne 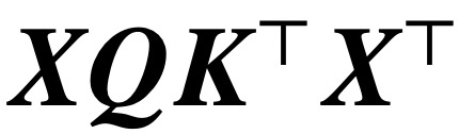 ; L'étude suppose que le premier jeton de Z (noté z) est utilisé pour la prédiction. Plus précisément, étant donné un ensemble de données d'entraînement
; L'étude suppose que le premier jeton de Z (noté z) est utilisé pour la prédiction. Plus précisément, étant donné un ensemble de données d'entraînement 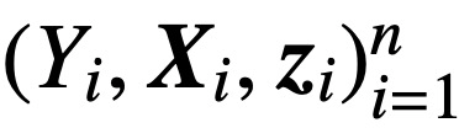 ,
, 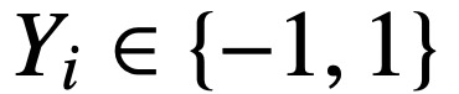 ,
, 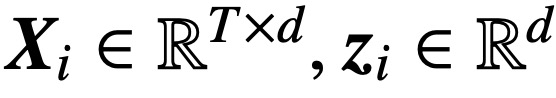 , cette étude utilise la fonction de perte décroissante
, cette étude utilise la fonction de perte décroissante  pour minimiser :
pour minimiser :
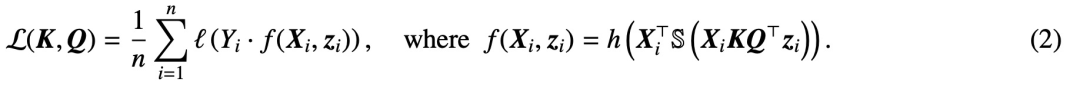
Ici, h (・) : 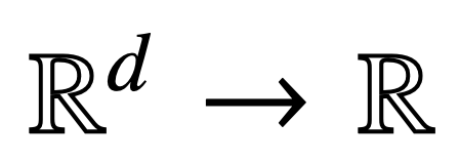 est l'en-tête de prédiction contenant la valeur poids V. Dans cette formulation, le modèle f (・) représente avec précision un transformateur monocouche où la couche d'attention est suivie d'un MLP. L'auteur restaure l'auto-attention dans (2) en posant
est l'en-tête de prédiction contenant la valeur poids V. Dans cette formulation, le modèle f (・) représente avec précision un transformateur monocouche où la couche d'attention est suivie d'un MLP. L'auteur restaure l'auto-attention dans (2) en posant 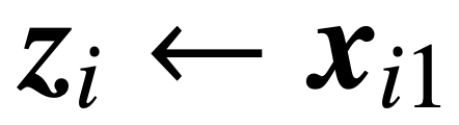 , où x_i représente le premier jeton de la séquence X_i. En raison de la nature non linéaire de l’opération softmax, elle pose un énorme défi en matière d’optimisation. Même si la tête de prédiction est fixe et linéaire, le problème est non convexe et non linéaire. Dans cette étude, les auteurs se concentrent sur l’optimisation des poids d’attention (K, Q ou W) et sur la résolution de ces défis pour établir l’équivalence de base des SVM.
, où x_i représente le premier jeton de la séquence X_i. En raison de la nature non linéaire de l’opération softmax, elle pose un énorme défi en matière d’optimisation. Même si la tête de prédiction est fixe et linéaire, le problème est non convexe et non linéaire. Dans cette étude, les auteurs se concentrent sur l’optimisation des poids d’attention (K, Q ou W) et sur la résolution de ces défis pour établir l’équivalence de base des SVM.
La structure de l'article est la suivante : le chapitre 2 introduit les connaissances préliminaires sur l'auto-attention et l'optimisation ; le chapitre 3 analyse la géométrie d'optimisation de l'auto-attention, montrant que le paramètre d'attention RP converge vers la solution marginale maximale ; Le chapitre 4 et le chapitre 5 présentent respectivement l'analyse de descente de gradient globale et locale, montrant que la variable de requête clé W converge vers la solution de (Att-SVM) ; le chapitre 6 fournit des résultats sur l'équivalence des têtes de prédiction non linéaires et du chapitre SVM généralisé ; Le chapitre 7 étend la théorie à la prédiction séquentielle et causale ; le chapitre 8 discute de la littérature connexe. Enfin, le chapitre 9 conclut en proposant des questions ouvertes et des orientations de recherche futures.
Le contenu principal de l'article est le suivant :
Biais implicite dans la couche d'attention (Chapitre 2-3)
Optimisation des paramètres d'attention (K, Q) lorsque la régularisation disparaît, convergera vers la solution marginale maximale de  dans la direction, et sa norme nucléaire cible est le paramètre de combinaison
dans la direction, et sa norme nucléaire cible est le paramètre de combinaison 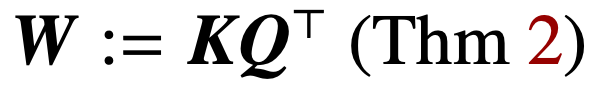 . Dans le cas du paramétrage direct de l'attention croisée avec le paramètre combiné W, le chemin de régularisation (RP) converge directionnellement vers la solution (Att-SVM) ciblant la norme de Frobenius.
. Dans le cas du paramétrage direct de l'attention croisée avec le paramètre combiné W, le chemin de régularisation (RP) converge directionnellement vers la solution (Att-SVM) ciblant la norme de Frobenius.
Il s'agit du premier résultat permettant de distinguer formellement les dynamiques d'optimisation paramétrique W versus (K, Q), révélant des biais d'ordre inférieur dans cette dernière. La théorie de cette étude décrit clairement l’optimalité des jetons sélectionnés et s’étend naturellement aux paramètres de classification séquence à séquence ou causale.
Convergence de la descente de gradient (Chapitre 4-5)
Avec une initialisation appropriée et une tête linéaire h (・), les itérations de descente de gradient (GD) de la variable de requête clé combinée W convergent dans la direction vers la solution optimale locale de (Att-SVM) (Section 5). Pour atteindre un optimum local, le jeton sélectionné doit avoir un score plus élevé que les jetons adjacents.
La direction optimale locale n'est pas nécessairement unique et peut être déterminée en fonction des caractéristiques géométriques du problème [TLZO23]. Comme contribution importante, les auteurs identifient les conditions géométriques qui garantissent la convergence vers l'optimum global (chapitre 4). Ces conditions incluent :
- Le meilleur jeton a une nette différence de score
- La direction initiale du dégradé est cohérente avec le meilleur jeton ;
De plus, l'article montre également que le surparamétrage (c'est-à-dire que la dimension d est grande et les mêmes conditions) en garantissant la faisabilité de (1) (Att-SVM) et (2) un effet bénin paysage d’optimisation (c’est-à-dire qu’il n’y a pas de points stationnaires ni de directions optimales locales parasites) pour catalyser la convergence globale (voir Section 5.2).
Les figures 1 et 2 illustrent cela.
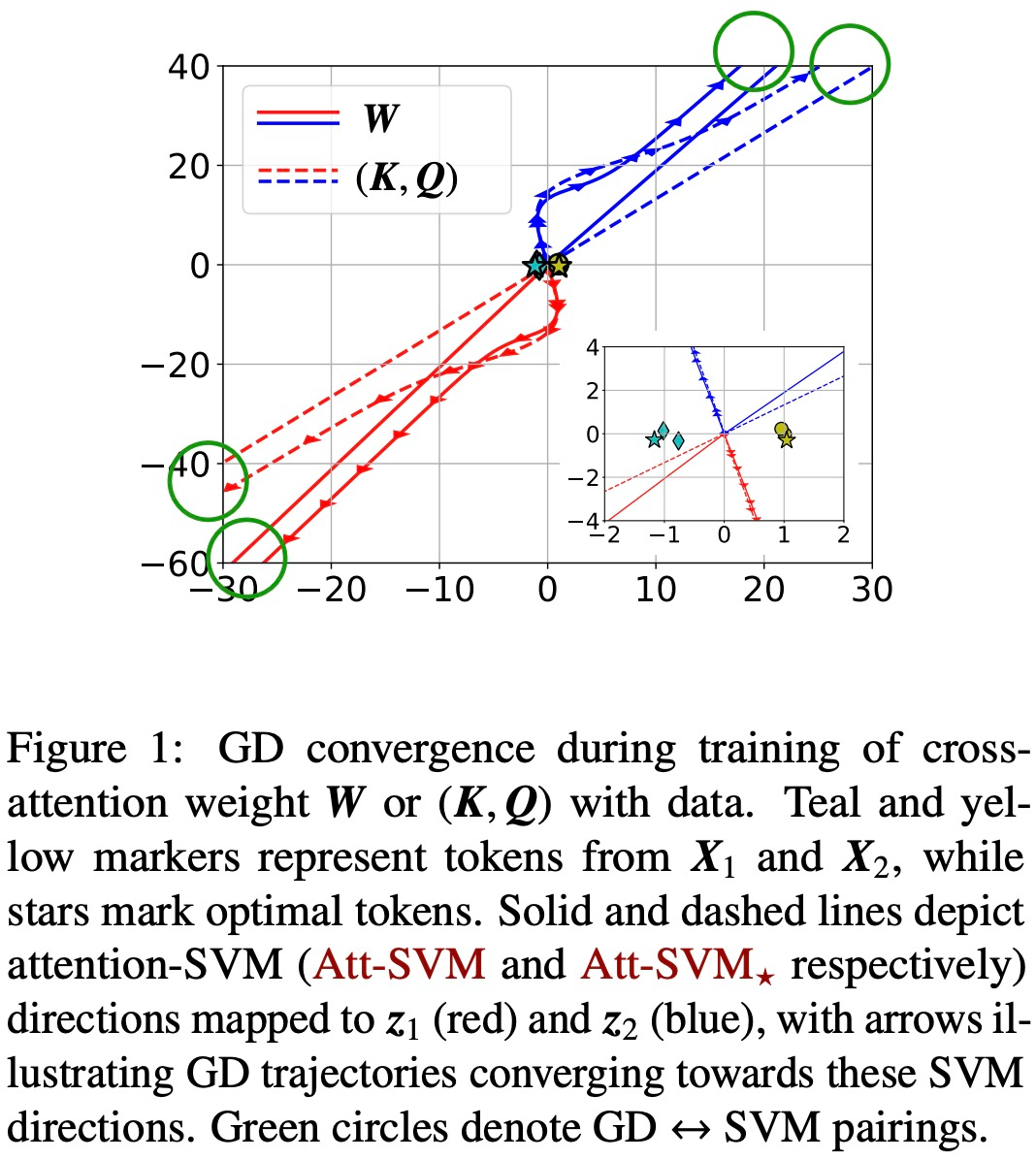
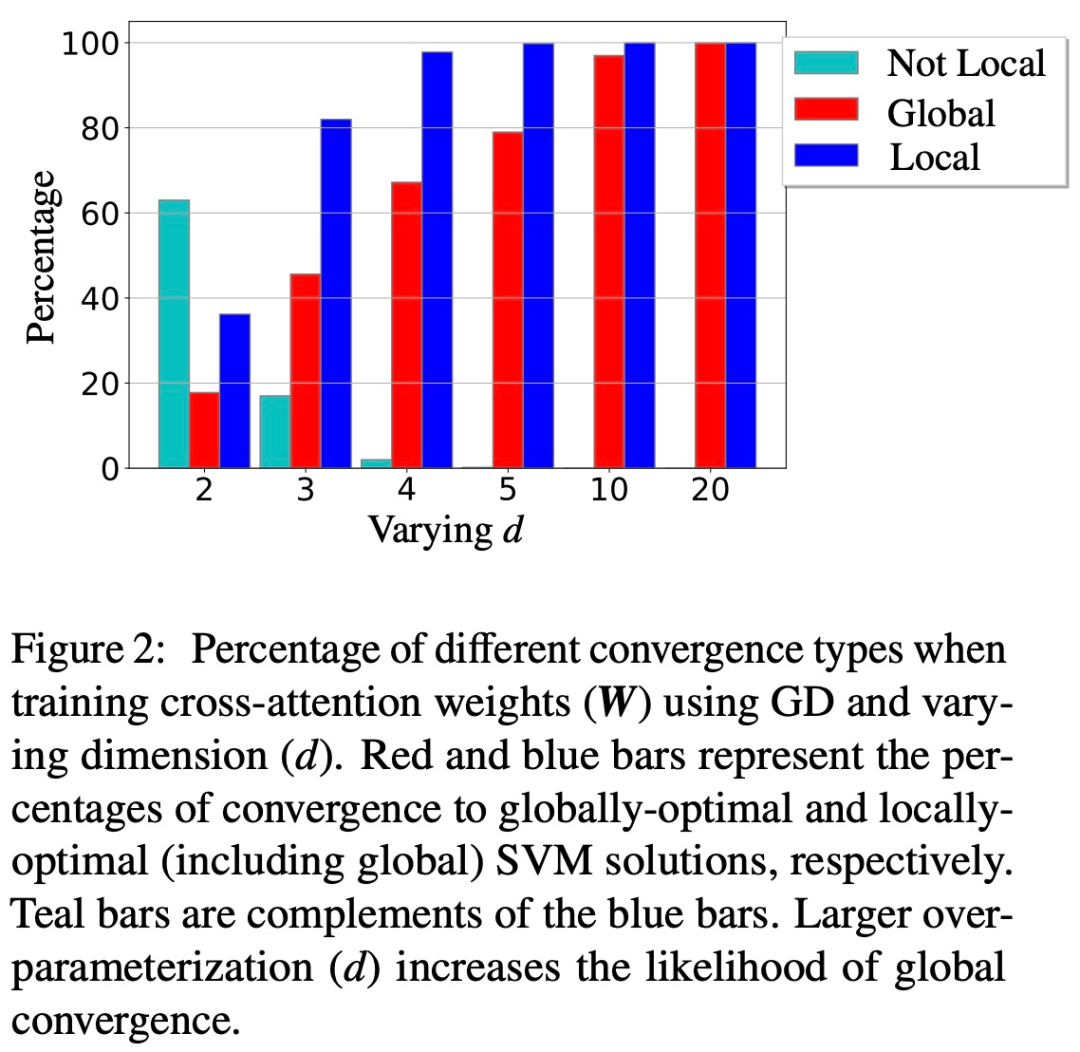
Généralité de l'équivalent SVM (Chapitre 6)
La couche d'attention est inhérente lors de l'optimisation avec h linéaire (・) Biais au sol pour sélectionner un jeton chaque séquence (c'est-à-dire une grande attention). Cela se reflète dans (Att-SVM), où le jeton de sortie est une combinaison convexe des jetons d'entrée. En revanche, les auteurs montrent que les têtes non linéaires doivent être composées de plusieurs jetons, soulignant ainsi leur importance dans la dynamique des transformateurs (Section 6.1). En utilisant les enseignements tirés de la théorie, les auteurs proposent une approche équivalente plus générale du SVM.
Notamment, ils démontrent que notre méthode peut prédire avec précision le biais implicite de l'attention entraînée via la descente de gradient dans des cas généraux non couverts par la théorie (par exemple, h (・) est un MLP). Plus précisément, notre formule générale découple le poids d'attention en deux parties : une partie directionnelle contrôlée par SVM, qui sélectionne les marqueurs en appliquant un masque 0-1 et une partie finie, qui ajuste la probabilité softmax pour déterminer la composition précise du jeton sélectionné ;
Une caractéristique importante de ces résultats est qu'ils s'appliquent à des ensembles de données arbitraires (tant que la SVM est réalisable) et peuvent être vérifiés numériquement. Les auteurs ont vérifié expérimentalement de manière approfondie l'équivalence marginale maximale et la polarisation implicite du transformateur. Les auteurs pensent que ces résultats contribuent à la compréhension des transformateurs en tant que mécanisme hiérarchique de sélection de jetons à marge maximale et peuvent jeter les bases des recherches à venir sur leur dynamique d’optimisation et de généralisation.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Open source! Au-delà de ZoeDepth ! DepthFM : estimation rapide et précise de la profondeur monoculaire !
Apr 03, 2024 pm 12:04 PM
Open source! Au-delà de ZoeDepth ! DepthFM : estimation rapide et précise de la profondeur monoculaire !
Apr 03, 2024 pm 12:04 PM
0. À quoi sert cet article ? Nous proposons DepthFM : un modèle d'estimation de profondeur monoculaire génératif de pointe, polyvalent et rapide. En plus des tâches traditionnelles d'estimation de la profondeur, DepthFM démontre également des capacités de pointe dans les tâches en aval telles que l'inpainting en profondeur. DepthFM est efficace et peut synthétiser des cartes de profondeur en quelques étapes d'inférence. Lisons ce travail ensemble ~ 1. Titre des informations sur l'article : DepthFM : FastMonocularDepthEstimationwithFlowMatching Auteur : MingGui, JohannesS.Fischer, UlrichPrestel, PingchuanMa, Dmytr
 Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Imaginez un modèle d'intelligence artificielle qui non seulement a la capacité de surpasser l'informatique traditionnelle, mais qui permet également d'obtenir des performances plus efficaces à moindre coût. Ce n'est pas de la science-fiction, DeepSeek-V2[1], le modèle MoE open source le plus puissant au monde est ici. DeepSeek-V2 est un puissant mélange de modèle de langage d'experts (MoE) présentant les caractéristiques d'une formation économique et d'une inférence efficace. Il est constitué de 236B paramètres, dont 21B servent à activer chaque marqueur. Par rapport à DeepSeek67B, DeepSeek-V2 offre des performances plus élevées, tout en économisant 42,5 % des coûts de formation, en réduisant le cache KV de 93,3 % et en augmentant le débit de génération maximal à 5,76 fois. DeepSeek est une entreprise explorant l'intelligence artificielle générale
 L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L’IA change effectivement les mathématiques. Récemment, Tao Zhexuan, qui a prêté une attention particulière à cette question, a transmis le dernier numéro du « Bulletin de l'American Mathematical Society » (Bulletin de l'American Mathematical Society). En se concentrant sur le thème « Les machines changeront-elles les mathématiques ? », de nombreux mathématiciens ont exprimé leurs opinions. L'ensemble du processus a été plein d'étincelles, intense et passionnant. L'auteur dispose d'une équipe solide, comprenant Akshay Venkatesh, lauréat de la médaille Fields, le mathématicien chinois Zheng Lejun, l'informaticien de l'Université de New York Ernest Davis et de nombreux autres universitaires bien connus du secteur. Le monde de l’IA a radicalement changé. Vous savez, bon nombre de ces articles ont été soumis il y a un an.
 Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Bonjour, Atlas électrique ! Le robot Boston Dynamics revient à la vie, des mouvements étranges à 180 degrés effraient Musk
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas entre officiellement dans l’ère des robots électriques ! Hier, l'Atlas hydraulique s'est retiré "en larmes" de la scène de l'histoire. Aujourd'hui, Boston Dynamics a annoncé que l'Atlas électrique était au travail. Il semble que dans le domaine des robots humanoïdes commerciaux, Boston Dynamics soit déterminé à concurrencer Tesla. Après la sortie de la nouvelle vidéo, elle a déjà été visionnée par plus d’un million de personnes en seulement dix heures. Les personnes âgées partent et de nouveaux rôles apparaissent. C'est une nécessité historique. Il ne fait aucun doute que cette année est l’année explosive des robots humanoïdes. Les internautes ont commenté : Les progrès des robots ont fait ressembler la cérémonie d'ouverture de cette année à des êtres humains, et le degré de liberté est bien plus grand que celui des humains. Mais n'est-ce vraiment pas un film d'horreur ? Au début de la vidéo, Atlas est allongé calmement sur le sol, apparemment sur le dos. Ce qui suit est à couper le souffle
 KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
Plus tôt ce mois-ci, des chercheurs du MIT et d'autres institutions ont proposé une alternative très prometteuse au MLP – KAN. KAN surpasse MLP en termes de précision et d’interprétabilité. Et il peut surpasser le MLP fonctionnant avec un plus grand nombre de paramètres avec un très petit nombre de paramètres. Par exemple, les auteurs ont déclaré avoir utilisé KAN pour reproduire les résultats de DeepMind avec un réseau plus petit et un degré d'automatisation plus élevé. Plus précisément, le MLP de DeepMind compte environ 300 000 paramètres, tandis que le KAN n'en compte qu'environ 200. KAN a une base mathématique solide comme MLP est basé sur le théorème d'approximation universelle, tandis que KAN est basé sur le théorème de représentation de Kolmogorov-Arnold. Comme le montre la figure ci-dessous, KAN a
 Vitesse Internet lente des données cellulaires sur iPhone : correctifs
May 03, 2024 pm 09:01 PM
Vitesse Internet lente des données cellulaires sur iPhone : correctifs
May 03, 2024 pm 09:01 PM
Vous êtes confronté à un décalage et à une connexion de données mobile lente sur iPhone ? En règle générale, la puissance de l'Internet cellulaire sur votre téléphone dépend de plusieurs facteurs tels que la région, le type de réseau cellulaire, le type d'itinérance, etc. Vous pouvez prendre certaines mesures pour obtenir une connexion Internet cellulaire plus rapide et plus fiable. Correctif 1 – Forcer le redémarrage de l'iPhone Parfois, le redémarrage forcé de votre appareil réinitialise simplement beaucoup de choses, y compris la connexion cellulaire. Étape 1 – Appuyez simplement une fois sur la touche d’augmentation du volume et relâchez-la. Ensuite, appuyez sur la touche de réduction du volume et relâchez-la à nouveau. Étape 2 – La partie suivante du processus consiste à maintenir le bouton sur le côté droit. Laissez l'iPhone finir de redémarrer. Activez les données cellulaires et vérifiez la vitesse du réseau. Vérifiez à nouveau Correctif 2 – Changer le mode de données Bien que la 5G offre de meilleures vitesses de réseau, elle fonctionne mieux lorsque le signal est plus faible
 La vitalité de la super intelligence s'éveille ! Mais avec l'arrivée de l'IA qui se met à jour automatiquement, les mères n'ont plus à se soucier des goulots d'étranglement des données.
Apr 29, 2024 pm 06:55 PM
La vitalité de la super intelligence s'éveille ! Mais avec l'arrivée de l'IA qui se met à jour automatiquement, les mères n'ont plus à se soucier des goulots d'étranglement des données.
Apr 29, 2024 pm 06:55 PM
Je pleure à mort. Le monde construit à la folie de grands modèles. Les données sur Internet ne suffisent pas du tout. Le modèle de formation ressemble à « The Hunger Games », et les chercheurs en IA du monde entier se demandent comment nourrir ces personnes avides de données. Ce problème est particulièrement important dans les tâches multimodales. À une époque où rien ne pouvait être fait, une équipe de start-up du département de l'Université Renmin de Chine a utilisé son propre nouveau modèle pour devenir la première en Chine à faire de « l'auto-alimentation des données générées par le modèle » une réalité. De plus, il s’agit d’une approche à deux volets, du côté compréhension et du côté génération, les deux côtés peuvent générer de nouvelles données multimodales de haute qualité et fournir un retour de données au modèle lui-même. Qu'est-ce qu'un modèle ? Awaker 1.0, un grand modèle multimodal qui vient d'apparaître sur le Forum Zhongguancun. Qui est l'équipe ? Moteur Sophon. Fondé par Gao Yizhao, doctorant à la Hillhouse School of Artificial Intelligence de l’Université Renmin.
 L'US Air Force présente son premier avion de combat IA de grande envergure ! Le ministre a personnellement effectué l'essai routier sans intervenir pendant tout le processus, et 100 000 lignes de code ont été testées 21 fois.
May 07, 2024 pm 05:00 PM
L'US Air Force présente son premier avion de combat IA de grande envergure ! Le ministre a personnellement effectué l'essai routier sans intervenir pendant tout le processus, et 100 000 lignes de code ont été testées 21 fois.
May 07, 2024 pm 05:00 PM
Récemment, le milieu militaire a été submergé par la nouvelle : les avions de combat militaires américains peuvent désormais mener des combats aériens entièrement automatiques grâce à l'IA. Oui, tout récemment, l’avion de combat IA de l’armée américaine a été rendu public pour la première fois, dévoilant ainsi son mystère. Le nom complet de ce chasseur est Variable Stability Simulator Test Aircraft (VISTA). Il a été personnellement piloté par le secrétaire de l'US Air Force pour simuler une bataille aérienne en tête-à-tête. Le 2 mai, le secrétaire de l'US Air Force, Frank Kendall, a décollé à bord d'un X-62AVISTA à la base aérienne d'Edwards. Notez que pendant le vol d'une heure, toutes les actions de vol ont été effectuées de manière autonome par l'IA ! Kendall a déclaré : "Au cours des dernières décennies, nous avons réfléchi au potentiel illimité du combat air-air autonome, mais cela a toujours semblé hors de portée." Mais maintenant,





