 Périphériques technologiques
Périphériques technologiques
 IA
IA
 ICCV 2023 Oral | Comment réaliser une formation de segments de test en monde ouvert ? Méthode d'auto-formation basée sur l'expansion dynamique de prototypes
ICCV 2023 Oral | Comment réaliser une formation de segments de test en monde ouvert ? Méthode d'auto-formation basée sur l'expansion dynamique de prototypes
ICCV 2023 Oral | Comment réaliser une formation de segments de test en monde ouvert ? Méthode d'auto-formation basée sur l'expansion dynamique de prototypes
Lors de la promotion de la mise en œuvre de méthodes de perception basées sur la vision, l'amélioration de la capacité de généralisation du modèle est une base importante. Formation/adaptation au moment du test (Test-Time Training/Adaptation) permet au modèle de s'adapter à la distribution des données du domaine cible inconnue en ajustant les poids des paramètres du modèle pendant la phase de test. Les méthodes TTT/TTA existantes se concentrent généralement sur l'amélioration des performances de formation des segments de test sous les données du domaine cible dans un environnement fermé. Cependant, dans de nombreux scénarios d'application, le domaine cible est facilement contaminé par des données hors domaine fortes (Strong OOD par exemple). , catégories de données sémantiquement non pertinentes. Dans ce cas, également connu sous le nom d'Open World Test Segment Training (OWTTT), les TTT/TTA existants classent généralement de force les données hors domaine fortes dans des catégories connues, interférant finalement avec les données hors domaine faibles (Weak OOD) telles que Capacité de reconnaissance des images perturbées par le bruit
Récemment, l'Université de technologie de Chine du Sud et l'équipe A*STAR ont proposé pour la première fois la mise en place d'une formation de segment de test en monde ouvert et ont lancé la méthode de formation correspondante

- Papier : https:/ /arxiv.org/abs/2308.09942
- Le contenu à réécrire est : Lien de code : https://github.com/Yushu-Li/OWTTT
- Cet article propose d'abord un seuil adaptatif fort La méthode de filtrage des échantillons de données hors domaine améliore la robustesse de la méthode TTT d'auto-formation dans le monde ouvert. Le procédé propose en outre une méthode pour caractériser des échantillons forts hors domaine sur la base de prototypes étendus dynamiquement afin d'améliorer l'effet de séparation de données hors domaine faible/fort. Enfin, l’autoformation est limitée par l’alignement de la distribution.
La méthode présentée dans cet article atteint des performances optimales sur 5 benchmarks OWTTT différents et fournit une nouvelle direction pour les recherches ultérieures sur le TTT afin d'explorer des méthodes TTT plus robustes. La recherche a été acceptée comme article oral à l’ICCV 2023.
IntroductionLa formation sur les segments de test (TTT) peut accéder aux données du domaine cible uniquement pendant la phase d'inférence et effectuer une inférence à la volée sur les données de test avec des changements de distribution. Le succès du TTT a été démontré sur un certain nombre de données de domaine cible artificiellement sélectionnées et corrompues. Cependant, les limites des capacités des méthodes TTT existantes n’ont pas été entièrement explorées.
Pour promouvoir les applications TTT dans des scénarios ouverts, la recherche s'est déplacée vers l'étude des scénarios dans lesquels les méthodes TTT peuvent échouer. De nombreux efforts ont été déployés pour développer des méthodes TTT stables et robustes dans des environnements de monde ouvert plus réalistes. Dans ce travail, nous explorons un scénario de monde ouvert courant mais négligé, dans lequel le domaine cible peut contenir des distributions de données de test tirées d'environnements significativement différents, tels que des catégories sémantiques différentes de celles du domaine source, ou simplement du bruit aléatoire.
Nous appelons les données de test ci-dessus des données fortes hors distribution (strong OOD). Ce que l'on appelle dans ce travail des données OOD faibles sont des données de test avec des changements de distribution, tels que des dommages synthétiques courants. Par conséquent, le manque de travaux existants sur cet environnement réel nous motive à explorer l'amélioration de la robustesse de l'Open World Test Segment Training (OWTTT), où les données de test sont contaminées par de forts échantillons OOD. être réécrit Il s'agit de : Figure 1 : Les résultats de l'évaluation de la méthode TTT existante dans le cadre OWTTT
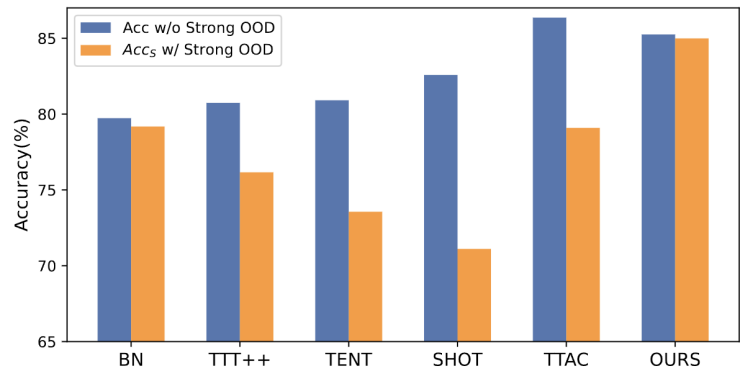
Le TTT basé sur l'auto-formation a du mal à gérer des échantillons OOD forts car il doit attribuer des échantillons de test à des classes connues. Bien que certains échantillons peu fiables puissent être filtrés en appliquant le seuil utilisé dans l’apprentissage semi-supervisé, il n’y a toujours aucune garantie que tous les échantillons OOD forts seront filtrés.
Les méthodes basées sur l'alignement de la distribution seront affectées lorsque des échantillons OOD forts sont calculés pour estimer la distribution du domaine cible. L'alignement de la distribution globale [1] et l'alignement de la distribution des classes [2] peuvent être affectés et conduire à un alignement inexact de la distribution des fonctionnalités.- Afin d'améliorer la robustesse du TTT en monde ouvert dans le cadre d'auto-formation, nous avons examiné les raisons potentielles de l'échec des méthodes TTT existantes et proposé une solution combinant deux technologiesTout d'abord, nous établirons le base de référence de TTT basée sur la variante, c'est-à-dire utiliser le prototype du domaine source comme centre de cluster pour le clustering dans le domaine cible. Pour atténuer le fort impact OOD de l'auto-entraînement à partir de faux pseudo-étiquettes, nous proposons une méthode sans hyperparamètres pour rejeter les échantillons OOD forts
- Pour séparer davantage les caractéristiques des échantillons OOD faibles et des échantillons OOD forts, nous autorisons le regroupement de prototypes pour isoler par sélection Une extension d'échantillon OOD forte. Par conséquent, l’auto-formation permettra aux échantillons OOD forts de former des groupes serrés autour du prototype OOD fort nouvellement développé. Cela facilitera l’alignement de la distribution entre les domaines source et cible. Nous proposons en outre de régulariser l'auto-formation grâce à un alignement de la distribution mondiale afin de réduire le risque de biais de confirmation
Enfin, afin de synthétiser le scénario TTT en monde ouvert, nous adoptons les ensembles de données CIFAR10-C, CIFAR100-C, ImageNet-C, VisDA-C, ImageNet-R, Tiny-ImageNet, MNIST et SVHN, et utilisons un data réglé sur Weak OOD, d’autres établissent des ensembles de données de référence pour une forte OOD. Nous appelons cette référence l'Open World Test Segment Training Benchmark et espérons que cela encouragera davantage de travaux futurs à se concentrer sur la robustesse de la formation des segments de test dans des scénarios plus réalistes.
Méthode
L'article est divisé en quatre parties pour présenter la méthode proposée.
1) Aperçu des paramètres des tâches de formation dans le segment de test en monde ouvert.
2) Présente comment utiliserLe clustering de prototypes est un algorithme d'apprentissage non supervisé utilisé pour regrouper des échantillons d'un ensemble de données en différentes catégories. Dans le clustering de prototypes, chaque catégorie est représentée par un ou plusieurs prototypes, qui peuvent être des échantillons dans l'ensemble de données ou générés selon certaines règles. Le but du clustering de prototypes est de réaliser un clustering en minimisant la distance entre les échantillons et les prototypes des catégories auxquelles ils appartiennent. Les algorithmes de clustering de prototypes courants incluent le clustering K-means et les modèles de mélange gaussien. Ces algorithmes sont largement utilisés dans des domaines tels que l'exploration de données, la reconnaissance de formes et le traitement d'images. Implémenter TTT et comment étendre le prototype pour la formation au temps de test en monde ouvert.
3) Présente comment utiliser les données du domaine cibleLe contenu qui doit être réécrit est : l'extension de prototype dynamique .
4) Présentation deDistribution Alignment avec Prototype Clustering est un algorithme d'apprentissage non supervisé utilisé pour regrouper des échantillons d'un ensemble de données en différentes catégories. Dans le clustering de prototypes, chaque catégorie est représentée par un ou plusieurs prototypes, qui peuvent être des échantillons dans l'ensemble de données ou générés selon certaines règles. Le but du clustering de prototypes est de réaliser un clustering en minimisant la distance entre les échantillons et les prototypes des catégories auxquelles ils appartiennent. Les algorithmes de clustering de prototypes courants incluent le clustering K-means et les modèles de mélange gaussien. Ces algorithmes, largement utilisés dans des domaines tels que l’exploration de données, la reconnaissance de formes et le traitement d’images, sont combinés pour permettre une formation puissante en temps de test en monde ouvert.

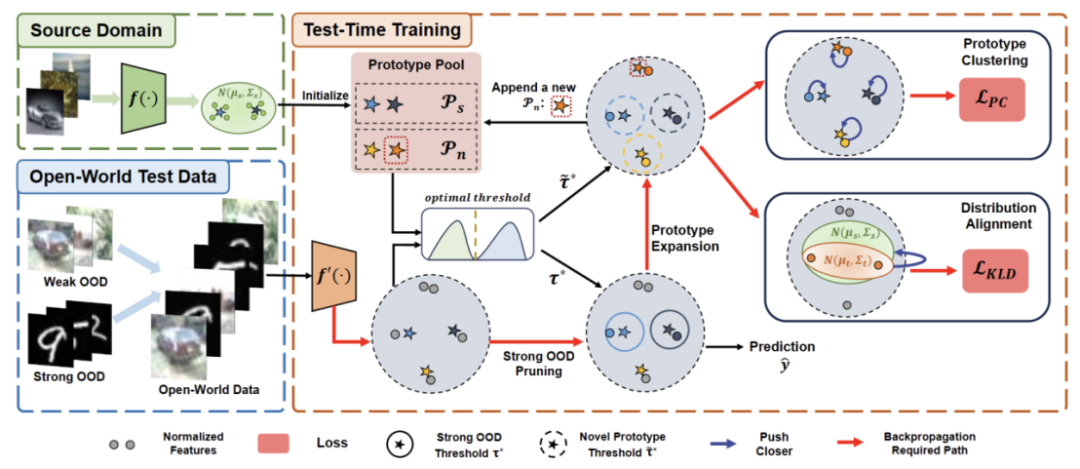
Le contenu qui doit être réécrit est : Figure 2 : Diagramme de présentation de la méthode
Paramètre de la tâche
L'objectif de TTT est d'adapter le modèle pré-entraîné du domaine source au domaine cible , où le domaine cible peut être relativement Il y a une migration de distribution dans le domaine source. Dans le TTT standard en monde fermé, les espaces d'étiquettes des domaines source et cible sont les mêmes. Cependant, dans le TTT en monde ouvert, l'espace d'étiquettes du domaine cible contient l'espace cible du domaine source, ce qui signifie que le domaine cible a de nouvelles catégories sémantiques inéditesPour éviter toute confusion entre les définitions de TTT, nous adoptons TTAC [2] Le protocole de formation au temps de test séquentiel (sTTT) proposé est évalué. Dans le cadre du protocole sTTT, les échantillons de test sont testés séquentiellement et les mises à jour du modèle sont effectuées après avoir observé de petits lots d'échantillons de test. La prédiction pour tout échantillon de test arrivant à l'horodatage t n'est pas affectée par tout échantillon de test arrivant à t+k (dont k est supérieur à 0).Le clustering de prototypes est un algorithme d'apprentissage non supervisé utilisé pour regrouper des échantillons d'un ensemble de données en différentes catégories. Dans le clustering de prototypes, chaque catégorie est représentée par un ou plusieurs prototypes, qui peuvent être des échantillons dans l'ensemble de données ou générés selon certaines règles. Le but du clustering de prototypes est de réaliser un clustering en minimisant la distance entre les échantillons et les prototypes des catégories auxquelles ils appartiennent. Les algorithmes de clustering de prototypes courants incluent le clustering K-means et les modèles de mélange gaussien. Ces algorithmes sont largement utilisés dans des domaines tels que l'exploration de données, la reconnaissance de formes et le traitement d'images.
Inspirés par les travaux utilisant le clustering dans les tâches d'adaptation de domaine [3,4], nous traitons la formation de segments de test comme la découverte de clusters dans la structure de données du domaine cible. . En identifiant des prototypes représentatifs en tant que centres de cluster, les structures de cluster sont identifiées dans le domaine cible et les échantillons de test sont encouragés à s'intégrer à proximité de l'un des prototypes. Le clustering de prototypes est un algorithme d'apprentissage non supervisé utilisé pour regrouper des échantillons d'un ensemble de données en différentes catégories. Dans le clustering de prototypes, chaque catégorie est représentée par un ou plusieurs prototypes, qui peuvent être des échantillons dans l'ensemble de données ou générés selon certaines règles. Le but du clustering de prototypes est de réaliser un clustering en minimisant la distance entre les échantillons et les prototypes des catégories auxquelles ils appartiennent. Les algorithmes de clustering de prototypes courants incluent le clustering K-means et les modèles de mélange gaussien. L'objectif de ces algorithmes, largement utilisés dans des domaines tels que l'exploration de données, la reconnaissance de formes et le traitement d'images, est défini comme minimisant la perte de log-vraisemblance négative de la similarité cosinus entre l'échantillon et le centre de l'amas, comme le montre le équation suivante.
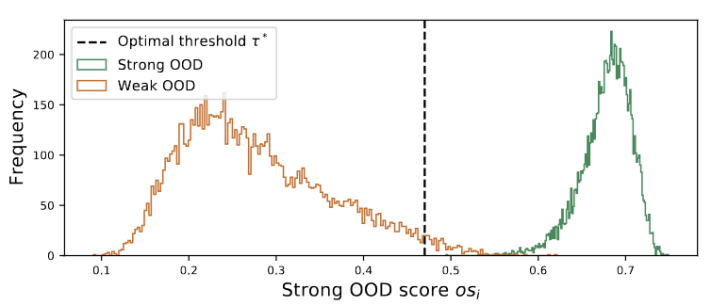
Figure 3 La valeur du groupe est distribuée en doubles pics

Nous observons que la valeur du groupe obéit à la distribution des doubles pics, comme le montre la figure 3. Par conséquent, au lieu de spécifier un seuil fixe, nous définissons le seuil optimal comme la meilleure valeur séparant les deux distributions. Plus précisément, le problème peut être formulé en divisant les valeurs aberrantes en deux groupes, et le seuil optimal minimisera la variance au sein du groupe. L'optimisation de l'équation suivante peut être réalisée efficacement en recherchant de manière exhaustive tous les seuils possibles de 0 à 1 par pas de 0,01. 
Ce qui doit être réécrit est : Extension de prototype dynamique
L'expansion du pool de prototypes OOD forts doit prendre en compte à la fois le domaine source et le prototype OOD fort pour évaluer l'échantillon de test. Pour estimer dynamiquement le nombre de clusters à partir des données, des études antérieures ont étudié des problèmes similaires. L'algorithme déterministe de clustering dur DP-means [5] a été développé en mesurant la distance des points de données aux centres de cluster connus, et un nouveau cluster est initialisé lorsque la distance est supérieure à un seuil. DP-means s'avère équivalent à l'optimisation de l'objectif K-means, mais avec une pénalité supplémentaire sur le nombre de clusters, fournissant une solution réalisable pour l'expansion dynamique de prototypes où une réécriture est nécessaire.
Pour atténuer la difficulté d'estimer des hyperparamètres supplémentaires, nous définissons d'abord un échantillon de test avec un score OOD fort étendu comme la distance la plus proche du prototype de domaine source existant et du prototype OOD fort, comme suit. Par conséquent, tester des échantillons au-dessus de ce seuil permettra de construire un nouveau prototype. Pour éviter d'ajouter des échantillons de test à proximité, nous répétons progressivement ce processus d'expansion du prototype. 
Avec d'autres prototypes OOD solides identifiés, nous avons défini des prototypes pour tester des échantillons. Le clustering est un algorithme d'apprentissage non supervisé utilisé pour regrouper des échantillons dans un ensemble de données en différentes catégories. Dans le clustering de prototypes, chaque catégorie est représentée par un ou plusieurs prototypes, qui peuvent être des échantillons dans l'ensemble de données ou générés selon certaines règles. Le but du clustering de prototypes est de réaliser un clustering en minimisant la distance entre les échantillons et les prototypes des catégories auxquelles ils appartiennent. Les algorithmes de clustering de prototypes courants incluent le clustering K-means et les modèles de mélange gaussien. Ces algorithmes sont largement utilisés dans des domaines tels que l'exploration de données, la reconnaissance de formes et le traitement d'images. La perte prend en compte deux facteurs. Premièrement, les échantillons de test classés dans des classes connues doivent être intégrés plus près des prototypes et plus éloignés des autres prototypes, ce qui définit la tâche de classification en classe K. Deuxièmement, les échantillons de test classés comme prototypes OOD forts doivent être éloignés de tout prototype du domaine source, ce qui définit la tâche de classification de classe K+1. En gardant ces objectifs à l’esprit, nous prototypons le clustering, un algorithme d’apprentissage non supervisé utilisé pour regrouper les échantillons d’un ensemble de données en catégories distinctes. Dans le clustering de prototypes, chaque catégorie est représentée par un ou plusieurs prototypes, qui peuvent être des échantillons dans l'ensemble de données ou générés selon certaines règles. Le but du clustering de prototypes est de réaliser un clustering en minimisant la distance entre les échantillons et les prototypes des catégories auxquelles ils appartiennent. Les algorithmes de clustering de prototypes courants incluent le clustering K-means et les modèles de mélange gaussien. Ces algorithmes sont largement utilisés dans des domaines tels que l'exploration de données, la reconnaissance de formes et le traitement d'images. La perte est définie comme suit.
Contraintes d'alignement de distribution

Il est bien connu que l'auto-formation est sensible aux pseudo-étiquettes erronées. La situation est aggravée lorsque le domaine cible est constitué d'échantillons OOD. Pour réduire le risque d'échec, nous utilisons en outre l'alignement de distribution [1] comme régularisation pour l'auto-formation, comme suit.

Expériences Nous testons sur 5 ensembles de données de référence OWTTT différents, y compris des ensembles de données synthétiques corrompus et des ensembles de données de style variable. L'expérience utilise principalement trois indicateurs d'évaluation : une faible précision de classification OOD ACCS, une forte précision de classification OOD ACCN et la moyenne harmonique des deux ACCH. Tableau 2 Performances des différentes méthodes sur l'ensemble de données Cifar100-C 
3 Performances des différentes méthodes sur l'ensemble de données ImageNet-C 
Tableau 4 Performances des différentes méthodes sur l'ensemble de données ImageNet-R 
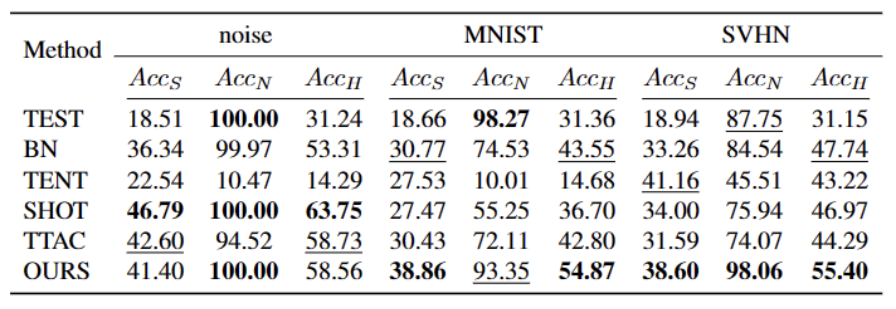
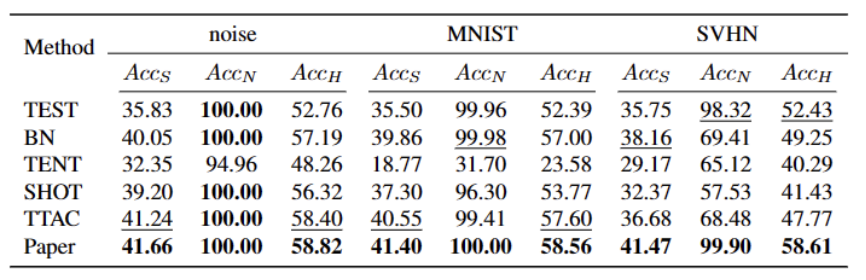
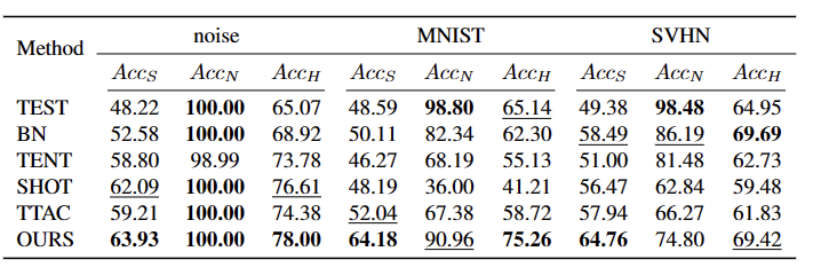
Tableau 5 Données VisDA-C des différentes méthodes Les performances de l'ensemble 
Comme le montre le tableau ci-dessus, notre méthode s'est grandement améliorée par rapport à la les meilleures méthodes actuelles sur presque tous les ensembles de données, et peuvent identifier efficacement les échantillons OOD forts et réduire leur impact sur la classification des échantillons OOD faibles. Notre méthode peut obtenir un TTT plus robuste dans des scénarios de monde ouvert. Lorsque vous résumez le contenu, vous devez conserver le sens original inchangé et réécrire la langue en chinois  Cet article propose pour la première fois les problèmes et les paramètres de l'Open World Test Segment Training (OWTTT), soulignant que les les méthodes sont inefficaces pour traiter les domaines contenant et source.Les données du domaine cible des échantillons OOD forts avec un décalage sémantique rencontreront souvent des difficultés, et une méthode d'auto-apprentissage basée sur la nécessité de réécrire le contenu est proposée pour résoudre les problèmes ci-dessus. Nous espérons que ce travail pourra fournir de nouvelles orientations pour les recherches ultérieures sur le TTT afin d'explorer des méthodes TTT plus robustes.
Cet article propose pour la première fois les problèmes et les paramètres de l'Open World Test Segment Training (OWTTT), soulignant que les les méthodes sont inefficaces pour traiter les domaines contenant et source.Les données du domaine cible des échantillons OOD forts avec un décalage sémantique rencontreront souvent des difficultés, et une méthode d'auto-apprentissage basée sur la nécessité de réécrire le contenu est proposée pour résoudre les problèmes ci-dessus. Nous espérons que ce travail pourra fournir de nouvelles orientations pour les recherches ultérieures sur le TTT afin d'explorer des méthodes TTT plus robustes. Références : [2] Yongyi Su, Xun Xu et Kui Jia Revisiter la formation réaliste au moment du test : inférence séquentielle et adaptation par clustering ancré dans Avancées dans les systèmes de traitement de l'information neuronale, 2022. .
[1] Yuejiang Liu, Parth Kothari, Bastien van Delft, Baptiste Bellot-Gurlet, Taylor Mordan et Alexandre Alahi : Quand la formation auto-supervisée pendant les tests échoue-t-elle ou réussit-elle ? Avancées dans les systèmes de traitement de l'information neuronale, 2021.[3] Tang Hui et Jia Kui. Adaptation discriminante du domaine contradictoire. Dans Actes de la conférence AAAI sur l'intelligence artificielle, volume 34, pages 5940-5947, 2020
[4] Kuniaki Saito, Shohei Yamamoto, Yoshitaka Ushiku et Tatsuya Harada Adaptation de domaine ouvert par rétropropagation. Vision par ordinateur, 2018.
[5] Brian Kulis et Michael I Jordan. Les k-means revisités : un nouvel algorithme via des méthodes bayésiennes non paramétriques. Lors de la Conférence internationale sur l'apprentissage automatique, 2012
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Un didacticiel sur le modèle de diffusion qui vaut votre temps, de l'Université Purdue
Apr 07, 2024 am 09:01 AM
Un didacticiel sur le modèle de diffusion qui vaut votre temps, de l'Université Purdue
Apr 07, 2024 am 09:01 AM
La diffusion permet non seulement de mieux imiter, mais aussi de « créer ». Le modèle de diffusion (DiffusionModel) est un modèle de génération d'images. Par rapport aux algorithmes bien connus tels que GAN et VAE dans le domaine de l’IA, le modèle de diffusion adopte une approche différente. Son idée principale est un processus consistant à ajouter d’abord du bruit à l’image, puis à la débruiter progressivement. Comment débruiter et restaurer l’image originale est la partie centrale de l’algorithme. L'algorithme final est capable de générer une image à partir d'une image bruitée aléatoirement. Ces dernières années, la croissance phénoménale de l’IA générative a permis de nombreuses applications passionnantes dans la génération de texte en image, la génération de vidéos, et bien plus encore. Le principe de base de ces outils génératifs est le concept de diffusion, un mécanisme d'échantillonnage spécial qui surmonte les limites des méthodes précédentes.
 Générez du PPT en un seul clic ! Kimi : Que les « travailleurs migrants PPT » deviennent d'abord populaires
Aug 01, 2024 pm 03:28 PM
Générez du PPT en un seul clic ! Kimi : Que les « travailleurs migrants PPT » deviennent d'abord populaires
Aug 01, 2024 pm 03:28 PM
Kimi : En une seule phrase, un PPT est prêt en seulement dix secondes. PPT est tellement ennuyeux ! Pour tenir une réunion, vous devez avoir un PPT ; pour rédiger un rapport hebdomadaire, vous devez avoir un PPT ; pour solliciter des investissements, vous devez présenter un PPT ; même pour accuser quelqu'un de tricherie, vous devez envoyer un PPT ; L'université ressemble plus à une spécialisation PPT. Vous regardez le PPT en classe et faites le PPT après les cours. Peut-être que lorsque Dennis Austin a inventé le PPT il y a 37 ans, il ne s'attendait pas à ce qu'un jour le PPT devienne aussi répandu. Parler de notre dure expérience de création de PPT nous fait monter les larmes aux yeux. "Il m'a fallu trois mois pour réaliser un PPT de plus de 20 pages, et je l'ai révisé des dizaines de fois. J'avais envie de vomir quand j'ai vu le PPT." "À mon apogée, je faisais cinq PPT par jour, et même ma respiration." était PPT." Si vous avez une réunion impromptue, vous devriez le faire
 Tous les prix CVPR 2024 annoncés ! Près de 10 000 personnes ont assisté à la conférence hors ligne et un chercheur chinois de Google a remporté le prix du meilleur article.
Jun 20, 2024 pm 05:43 PM
Tous les prix CVPR 2024 annoncés ! Près de 10 000 personnes ont assisté à la conférence hors ligne et un chercheur chinois de Google a remporté le prix du meilleur article.
Jun 20, 2024 pm 05:43 PM
Tôt le matin du 20 juin, heure de Pékin, CVPR2024, la plus grande conférence internationale sur la vision par ordinateur qui s'est tenue à Seattle, a officiellement annoncé le meilleur article et d'autres récompenses. Cette année, un total de 10 articles ont remporté des prix, dont 2 meilleurs articles et 2 meilleurs articles étudiants. De plus, il y a eu 2 nominations pour les meilleurs articles et 4 nominations pour les meilleurs articles étudiants. La conférence la plus importante dans le domaine de la vision par ordinateur (CV) est la CVPR, qui attire chaque année un grand nombre d'instituts de recherche et d'universités. Selon les statistiques, un total de 11 532 articles ont été soumis cette année, dont 2 719 ont été acceptés, avec un taux d'acceptation de 23,6 %. Selon l'analyse statistique des données CVPR2024 du Georgia Institute of Technology, du point de vue des sujets de recherche, le plus grand nombre d'articles est la synthèse et la génération d'images et de vidéos (Imageandvideosyn
 Du bare metal au grand modèle avec 70 milliards de paramètres, voici un tutoriel et des scripts prêts à l'emploi
Jul 24, 2024 pm 08:13 PM
Du bare metal au grand modèle avec 70 milliards de paramètres, voici un tutoriel et des scripts prêts à l'emploi
Jul 24, 2024 pm 08:13 PM
Nous savons que le LLM est formé sur des clusters informatiques à grande échelle utilisant des données massives. Ce site a présenté de nombreuses méthodes et technologies utilisées pour aider et améliorer le processus de formation LLM. Aujourd'hui, ce que nous souhaitons partager est un article qui approfondit la technologie sous-jacente et présente comment transformer un ensemble de « bare metals » sans même un système d'exploitation en un cluster informatique pour la formation LLM. Cet article provient d'Imbue, une startup d'IA qui s'efforce d'atteindre une intelligence générale en comprenant comment les machines pensent. Bien sûr, transformer un tas de « bare metal » sans système d'exploitation en un cluster informatique pour la formation LLM n'est pas un processus facile, plein d'exploration et d'essais et d'erreurs, mais Imbue a finalement réussi à former un LLM avec 70 milliards de paramètres et dans. le processus s'accumule
 Guide d'installation de PyCharm Community Edition : maîtrisez rapidement toutes les étapes
Jan 27, 2024 am 09:10 AM
Guide d'installation de PyCharm Community Edition : maîtrisez rapidement toutes les étapes
Jan 27, 2024 am 09:10 AM
Démarrage rapide avec PyCharm Community Edition : Tutoriel d'installation détaillé Analyse complète Introduction : PyCharm est un puissant environnement de développement intégré (IDE) Python qui fournit un ensemble complet d'outils pour aider les développeurs à écrire du code Python plus efficacement. Cet article présentera en détail comment installer PyCharm Community Edition et fournira des exemples de code spécifiques pour aider les débutants à démarrer rapidement. Étape 1 : Téléchargez et installez PyCharm Community Edition Pour utiliser PyCharm, vous devez d'abord le télécharger depuis son site officiel
 Cinq logiciels de programmation pour débuter l'apprentissage du langage C
Feb 19, 2024 pm 04:51 PM
Cinq logiciels de programmation pour débuter l'apprentissage du langage C
Feb 19, 2024 pm 04:51 PM
En tant que langage de programmation largement utilisé, le langage C est l'un des langages de base qui doivent être appris pour ceux qui souhaitent se lancer dans la programmation informatique. Cependant, pour les débutants, l’apprentissage d’un nouveau langage de programmation peut s’avérer quelque peu difficile, notamment en raison du manque d’outils d’apprentissage et de matériel pédagogique pertinents. Dans cet article, je présenterai cinq logiciels de programmation pour aider les débutants à démarrer avec le langage C et vous aider à démarrer rapidement. Le premier logiciel de programmation était Code :: Blocks. Code::Blocks est un environnement de développement intégré (IDE) gratuit et open source pour
 A lire absolument pour les débutants en technique : Analyse des niveaux de difficulté du langage C et Python
Mar 22, 2024 am 10:21 AM
A lire absolument pour les débutants en technique : Analyse des niveaux de difficulté du langage C et Python
Mar 22, 2024 am 10:21 AM
Titre : Une lecture incontournable pour les débutants en technique : Analyse des difficultés du langage C et de Python, nécessitant des exemples de code spécifiques. À l'ère numérique d'aujourd'hui, la technologie de programmation est devenue une capacité de plus en plus importante. Que vous souhaitiez travailler dans des domaines tels que le développement de logiciels, l'analyse de données, l'intelligence artificielle ou simplement apprendre la programmation par intérêt, choisir un langage de programmation adapté est la première étape. Parmi les nombreux langages de programmation, le langage C et Python sont deux langages de programmation largement utilisés, chacun ayant ses propres caractéristiques. Cet article analysera les niveaux de difficulté du langage C et Python
 L'IA utilisée | L'IA a créé un vlog sur la vie d'une fille vivant seule, qui a reçu des dizaines de milliers de likes en 3 jours
Aug 07, 2024 pm 10:53 PM
L'IA utilisée | L'IA a créé un vlog sur la vie d'une fille vivant seule, qui a reçu des dizaines de milliers de likes en 3 jours
Aug 07, 2024 pm 10:53 PM
Rédacteur du Machine Power Report : Yang Wen La vague d’intelligence artificielle représentée par les grands modèles et l’AIGC a discrètement changé notre façon de vivre et de travailler, mais la plupart des gens ne savent toujours pas comment l’utiliser. C'est pourquoi nous avons lancé la rubrique « AI in Use » pour présenter en détail comment utiliser l'IA à travers des cas d'utilisation de l'intelligence artificielle intuitifs, intéressants et concis et stimuler la réflexion de chacun. Nous invitons également les lecteurs à soumettre des cas d'utilisation innovants et pratiques. Lien vidéo : https://mp.weixin.qq.com/s/2hX_i7li3RqdE4u016yGhQ Récemment, le vlog de la vie d'une fille vivant seule est devenu populaire sur Xiaohongshu. Une animation de style illustration, associée à quelques mots de guérison, peut être facilement récupérée en quelques jours seulement.



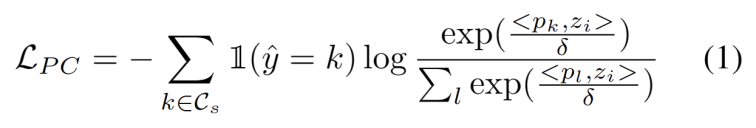
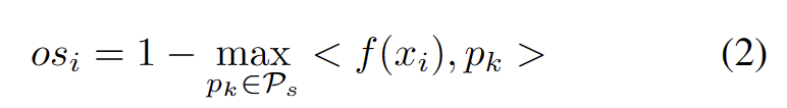
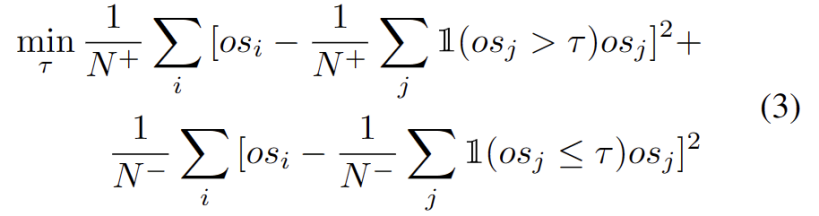
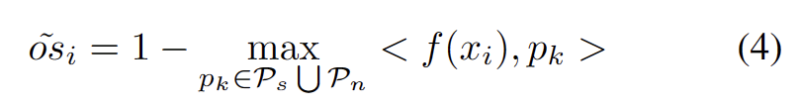
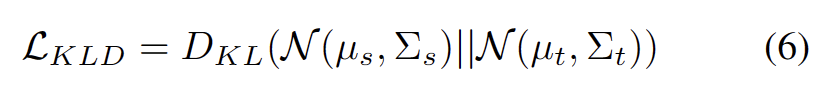


 Cet article propose pour la première fois les problèmes et les paramètres de l'Open World Test Segment Training (OWTTT), soulignant que les les méthodes sont inefficaces pour traiter les domaines contenant et source.Les données du domaine cible des échantillons OOD forts avec un décalage sémantique rencontreront souvent des difficultés, et une méthode d'auto-apprentissage basée sur la nécessité de réécrire le contenu est proposée pour résoudre les problèmes ci-dessus. Nous espérons que ce travail pourra fournir de nouvelles orientations pour les recherches ultérieures sur le TTT afin d'explorer des méthodes TTT plus robustes.
Cet article propose pour la première fois les problèmes et les paramètres de l'Open World Test Segment Training (OWTTT), soulignant que les les méthodes sont inefficaces pour traiter les domaines contenant et source.Les données du domaine cible des échantillons OOD forts avec un décalage sémantique rencontreront souvent des difficultés, et une méthode d'auto-apprentissage basée sur la nécessité de réécrire le contenu est proposée pour résoudre les problèmes ci-dessus. Nous espérons que ce travail pourra fournir de nouvelles orientations pour les recherches ultérieures sur le TTT afin d'explorer des méthodes TTT plus robustes. 

