 interface Web
interface Web
 js tutoriel
js tutoriel
 Programme JavaScript pour calculer efficacement la somme des diagonales de la matrice
Programme JavaScript pour calculer efficacement la somme des diagonales de la matrice
Programme JavaScript pour calculer efficacement la somme des diagonales de la matrice

Nous allons écrire un programme en JavaScript pour calculer efficacement la somme des diagonales d'une matrice. Pour ce faire, nous utiliserons une structure de boucle pour parcourir la matrice et ajouter des éléments situés aux positions correspondant aux diagonales. En tirant parti des propriétés mathématiques des matrices, nous pouvons minimiser la quantité de calculs nécessaires pour additionner les diagonales. Avec cette approche, nous serons capables de gérer des matrices de différentes tailles de manière efficace sur le plan informatique.
Méthode
Pour calculer la somme des diagonales d'une matrice, il faut additionner les valeurs des éléments de la diagonale principale (en haut à gauche vers en bas à droite) et de la diagonale secondaire (en haut à droite vers en bas - gauche)
Vous pouvez utiliser une approche à double boucle où une boucle traverse les lignes et la deuxième boucle traverse les colonnes pour accéder aux éléments en diagonale.
Nous pouvons conserver deux variables pour stocker la somme des éléments respectivement sur la diagonale principale et la sous-diagonale.
-
Pour accéder aux éléments de la diagonale principale, nous devons ajouter l'index de ligne et l'index de colonne actuels, tandis que pour les éléments de la diagonale secondaire, nous devons soustraire l'index de colonne de l'index de ligne.
李> Enfin, nous renvoyons la somme des deux variables comme résultat, ce qui donnera la somme des éléments sur les deux diagonales de la matrice.
Exemple
Voici un exemple de programme JavaScript qui calcule efficacement la somme des diagonales d'une matrice -
function diagonalSum(matrix) {
let sum = 0;
let n = matrix.length;
for (let i = 0; i < n; i++) {
sum += matrix[i][i];
sum += matrix[i][n - i - 1];
}
if (n % 2 !== 0) {
let mid = Math.floor(n / 2);
sum -= matrix[mid][mid];
}
return sum;
}
const matrix = [[1, 2, 3],[4, 5, 6], [7, 8, 9]];
console.log(diagonalSum(matrix));
Instructions
Initialisez la variable sum pour stocker la somme des diagonales, et initialisez la variable n pour stocker le nombre de lignes dans la matrice.
Utilisez une boucle for pour parcourir la matrice, en ajoutant les valeurs diagonales à sum. Pour chaque itération i, on ajoute la diagonale principale matrix[ i][i] et l'anti-diagonale matrix[i][n - i - 1].
Si le nombre de lignes de la matrice est impair, on soustrait la valeur du milieu matrix[mid][mid] (où mid est l'indice de la ligne du milieu, calculé à l'aide de Math.floor(n / 2 )) car il sera ajouté deux fois.
Renvoie la valeur de la somme.
La complexité temporelle de cet algorithme est O(n), ce qui en fait une solution efficace pour calculer la somme des diagonales de la matrice.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Remplacer les caractères de chaîne en javascript
Mar 11, 2025 am 12:07 AM
Remplacer les caractères de chaîne en javascript
Mar 11, 2025 am 12:07 AM
Explication détaillée de la méthode de remplacement de la chaîne JavaScript et de la FAQ Cet article explorera deux façons de remplacer les caractères de chaîne dans JavaScript: le code JavaScript interne et le HTML interne pour les pages Web. Remplacer la chaîne dans le code JavaScript Le moyen le plus direct consiste à utiliser la méthode Remplace (): str = str.replace ("trouver", "remplacer"); Cette méthode remplace uniquement la première correspondance. Pour remplacer toutes les correspondances, utilisez une expression régulière et ajoutez le drapeau global G: str = str.replace (/ fi
 Tutoriel de configuration de l'API de recherche Google personnalisé
Mar 04, 2025 am 01:06 AM
Tutoriel de configuration de l'API de recherche Google personnalisé
Mar 04, 2025 am 01:06 AM
Ce tutoriel vous montre comment intégrer une API de recherche Google personnalisée dans votre blog ou site Web, offrant une expérience de recherche plus raffinée que les fonctions de recherche de thème WordPress standard. C'est étonnamment facile! Vous pourrez restreindre les recherches à Y
 8 Superbes plugins de mise en page JQuery Page
Mar 06, 2025 am 12:48 AM
8 Superbes plugins de mise en page JQuery Page
Mar 06, 2025 am 12:48 AM
Tirez parti de jQuery pour les dispositions de page Web sans effort: 8 plugins essentiels JQuery simplifie considérablement la mise en page de la page Web. Cet article met en évidence huit puissants plugins jQuery qui rationalisent le processus, particulièrement utile pour la création de sites Web manuels
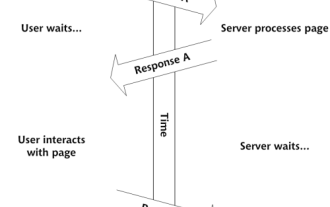 Créez vos propres applications Web Ajax
Mar 09, 2025 am 12:11 AM
Créez vos propres applications Web Ajax
Mar 09, 2025 am 12:11 AM
Vous voici donc, prêt à tout savoir sur cette chose appelée Ajax. Mais qu'est-ce que c'est exactement? Le terme Ajax fait référence à un regroupement lâche de technologies utilisées pour créer un contenu Web interactif dynamique. Le terme Ajax, inventé à l'origine par Jesse J
 Qu'est-ce que & # x27; ceci & # x27; en javascript?
Mar 04, 2025 am 01:15 AM
Qu'est-ce que & # x27; ceci & # x27; en javascript?
Mar 04, 2025 am 01:15 AM
Points de base Ceci dans JavaScript fait généralement référence à un objet qui "possède" la méthode, mais cela dépend de la façon dont la fonction est appelée. Lorsqu'il n'y a pas d'objet actuel, cela fait référence à l'objet global. Dans un navigateur Web, il est représenté par Window. Lorsque vous appelez une fonction, cela maintient l'objet global; mais lors de l'appel d'un constructeur d'objets ou de l'une de ses méthodes, cela fait référence à une instance de l'objet. Vous pouvez modifier le contexte de ceci en utilisant des méthodes telles que Call (), Appliquer () et Bind (). Ces méthodes appellent la fonction en utilisant la valeur et les paramètres donnés. JavaScript est un excellent langage de programmation. Il y a quelques années, cette phrase était
 10 feuilles de triche mobiles pour le développement mobile
Mar 05, 2025 am 12:43 AM
10 feuilles de triche mobiles pour le développement mobile
Mar 05, 2025 am 12:43 AM
Ce message compile des feuilles de triche utiles, des guides de référence, des recettes rapides et des extraits de code pour le développement d'Android, BlackBerry et Iphone. Aucun développeur ne devrait être sans eux! Guide de référence sur les gestes touchés (PDF) Une ressource précieuse pour Desig
 Améliorez vos connaissances jQuery avec le spectateur source
Mar 05, 2025 am 12:54 AM
Améliorez vos connaissances jQuery avec le spectateur source
Mar 05, 2025 am 12:54 AM
JQuery est un excellent cadre JavaScript. Cependant, comme pour n'importe quelle bibliothèque, il est parfois nécessaire de passer sous le capot pour découvrir ce qui se passe. C'est peut-être parce que vous tracez un bug ou que vous êtes simplement curieux de savoir comment jQuery réalise une interface utilisateur particulière
 Comment créer et publier mes propres bibliothèques JavaScript?
Mar 18, 2025 pm 03:12 PM
Comment créer et publier mes propres bibliothèques JavaScript?
Mar 18, 2025 pm 03:12 PM
L'article discute de la création, de la publication et du maintien des bibliothèques JavaScript, en se concentrant sur la planification, le développement, les tests, la documentation et les stratégies de promotion.





