 développement back-end
développement back-end
 tutoriel php
tutoriel php
 Analyse de l'algorithme PHP : Comment utiliser un algorithme de programmation dynamique pour résoudre le problème du sac à dos 0-1 ?
Analyse de l'algorithme PHP : Comment utiliser un algorithme de programmation dynamique pour résoudre le problème du sac à dos 0-1 ?
Analyse de l'algorithme PHP : Comment utiliser un algorithme de programmation dynamique pour résoudre le problème du sac à dos 0-1 ?

Analyse de l'algorithme PHP : Comment utiliser un algorithme de programmation dynamique pour résoudre le problème du sac à dos 0-1 ?
Introduction :
La programmation dynamique est une idée algorithmique couramment utilisée pour résoudre des problèmes d'optimisation. Dans le développement de programmes, le problème du sac à dos 0-1 est un scénario classique d’application de programmation dynamique. Cet article explique comment utiliser PHP pour écrire un algorithme de programmation dynamique afin de résoudre le problème du sac à dos 0-1 et fournit des exemples de code spécifiques.
Quel est le problème du sac à dos 0-1 ?
Le problème du sac à dos 0-1 est un problème d'optimisation combinatoire classique. Le problème se pose comme suit : Il existe un sac à dos d’une capacité de C. Il y a n éléments, chaque élément a un poids w[i] et une valeur v[i]. Il est nécessaire de choisir une combinaison d’articles pour maximiser la valeur totale sans dépasser la capacité du sac à dos.
Solution de programmation dynamique
L'algorithme de programmation dynamique consiste à diviser le problème donné en une série de sous-problèmes et à stocker les solutions optimales des sous-problèmes, et enfin à résoudre la solution optimale de l'ensemble du problème. Pour le problème du sac à dos 0-1, nous pouvons utiliser un algorithme de programmation dynamique pour le résoudre.
Idée d'algorithme :
- Créez un tableau bidimensionnel dp, dpi représente la valeur maximale lorsque seuls les i premiers éléments sont pris en compte et que la capacité du sac à dos est j.
- Initialisez le tableau dp en définissant tous les éléments sur 0.
-
Articles de traversée :
- Pour chaque article, si son poids est inférieur ou égal à la capacité du sac à dos j, vous devez comparer la valeur lorsque l'article est mis et lorsque l'article n'est pas mis, et choisir la solution la plus large pour mettre à jour le tableau dp.
- Si le poids de l'article est supérieur à la capacité du sac à dos j, vous pouvez seulement choisir de ne pas mettre l'article dedans, c'est-à-dire dpi = dpi-1.
- Une fois le cycle terminé, dpn est la valeur maximale lorsque la capacité du sac à dos est C.
Exemple de code spécifique :
function knapsack($C, $weight, $value, $n) {
$dp = array();
for ($i = 0; $i <= $n; $i++) {
for ($j = 0; $j <= $C; $j++) {
$dp[$i][$j] = 0;
}
}
for ($i = 1; $i <= $n; $i++) {
for ($j = 1; $j <= $C; $j++) {
if ($weight[$i-1] <= $j) {
$dp[$i][$j] = max($value[$i-1] + $dp[$i-1][$j-$weight[$i-1]], $dp[$i-1][$j]);
} else {
$dp[$i][$j] = $dp[$i-1][$j];
}
}
}
return $dp[$n][$C];
}
// 示例输入
$C = 10; // 背包容量
$weight = array(2, 3, 4, 5); // 物品重量
$value = array(3, 4, 5, 6); // 物品价值
$n = count($weight); // 物品数量
// 输出最大价值
echo "背包容量为 " . $C . " 时的最大价值为:" . knapsack($C, $weight, $value, $n);Analyse du code :
- fonction
knapsackaccepte quatre paramètres : capacité du sac à dos C, poids du tableau de poids de l'article, valeur du tableau de valeurs de l'article et quantité d'article n. - Créez un tableau bidimensionnel $dp pour stocker la solution optimale au sous-problème.
- Initialisez le tableau dp en définissant tous les éléments sur 0.
- Parcourez les éléments et effectuez des jugements et des mises à jour basés sur l'équation de transition d'état de la programmation dynamique.
- Une fois la boucle terminée, le dpn renvoyé est la valeur maximale lorsque la capacité du sac à dos est C.
Conclusion :
En utilisant un algorithme de programmation dynamique pour résoudre le problème du sac à dos 0-1, la valeur maximale que le sac à dos peut contenir peut être résolue efficacement. En PHP, cet algorithme peut être implémenté en écrivant du code approprié. Cette idée algorithmique n’est pas seulement applicable au problème du sac à dos 0-1, mais peut également être appliquée à d’autres problèmes d’optimisation combinatoire similaires.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment écrire un algorithme de programmation dynamique en utilisant C#
Sep 20, 2023 pm 04:03 PM
Comment écrire un algorithme de programmation dynamique en utilisant C#
Sep 20, 2023 pm 04:03 PM
Comment utiliser C# pour écrire un algorithme de programmation dynamique Résumé : La programmation dynamique est un algorithme courant pour résoudre des problèmes d'optimisation et convient à une variété de scénarios. Cet article explique comment utiliser C# pour écrire des algorithmes de programmation dynamique et fournit des exemples de code spécifiques. 1. Qu'est-ce qu'un algorithme de programmation dynamique ? La programmation dynamique (DP) est une idée algorithmique utilisée pour résoudre des problèmes avec des sous-problèmes qui se chevauchent et des propriétés de sous-structure optimales. La programmation dynamique décompose le problème en plusieurs sous-problèmes à résoudre et enregistre la solution à chaque sous-problème.
 Analyse d'algorithme PHP : Comment utiliser un algorithme de programmation dynamique pour résoudre le problème de sous-chaîne palindrome la plus longue ?
Sep 19, 2023 pm 12:19 PM
Analyse d'algorithme PHP : Comment utiliser un algorithme de programmation dynamique pour résoudre le problème de sous-chaîne palindrome la plus longue ?
Sep 19, 2023 pm 12:19 PM
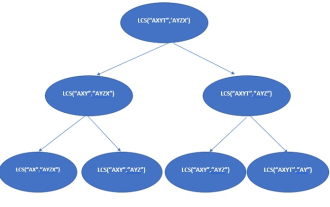
Analyse d'algorithme PHP : Comment utiliser un algorithme de programmation dynamique pour résoudre le problème de sous-chaîne palindrome la plus longue ? La programmation dynamique (programmation dynamique) est une idée d'algorithme couramment utilisée qui peut résoudre de nombreux problèmes complexes. L’un d’eux est le problème de la sous-chaîne palindrome la plus longue, qui consiste à trouver la longueur de la sous-chaîne palindrome la plus longue dans une chaîne. Cet article explique comment utiliser PHP pour écrire un algorithme de programmation dynamique afin de résoudre ce problème et fournit des exemples de code spécifiques. Définissons d’abord la sous-chaîne palindrome la plus longue. Une chaîne palindrome fait référence à une chaîne qui lit la même chose vers l'avant et vers l'arrière, et la chaîne palindrome
 Comment utiliser l'algorithme du problème du sac à dos en C++
Sep 21, 2023 pm 02:18 PM
Comment utiliser l'algorithme du problème du sac à dos en C++
Sep 21, 2023 pm 02:18 PM
Comment utiliser l'algorithme du problème du sac à dos en C++ Le problème du sac à dos est l'un des problèmes classiques des algorithmes informatiques. Il implique la manière de sélectionner certains éléments à mettre dans le sac à dos en fonction d'une capacité donnée du sac à dos afin de maximiser la valeur totale des éléments. Cet article présentera en détail comment utiliser l'algorithme de programmation dynamique en C++ pour résoudre le problème du sac à dos et donnera des exemples de code spécifiques. Tout d’abord, nous devons définir l’entrée et la sortie du problème du sac à dos. L'entrée inclut le tableau de poids wt[] de l'article, le tableau de valeurs val[] de l'article et la capacité W du sac à dos. Le résultat est quels objets sont sélectionnés
 Quels sont les algorithmes courants dans la programmation PHP ?
Jun 12, 2023 am 08:30 AM
Quels sont les algorithmes courants dans la programmation PHP ?
Jun 12, 2023 am 08:30 AM
En programmation PHP, les algorithmes font partie intégrante. La maîtrise des algorithmes courants peut non seulement améliorer l’efficacité du code, mais également faciliter la conception ultérieure des programmes. Les algorithmes suivants sont courants dans la programmation PHP : Algorithme de tri L'algorithme de tri fait référence à l'organisation d'un ensemble de données dans une séquence ordonnée selon certaines règles. Dans la programmation PHP, les algorithmes de tri couramment utilisés incluent le tri à bulles, le tri par insertion, le tri par sélection, le tri rapide, etc. Parmi eux, le tri rapide est l'algorithme de tri ayant la complexité temporelle la plus faible et convient au traitement de données à grande échelle. algorithme de recherche algorithme de recherche
 Comment résoudre le problème du sac à dos en PHP en utilisant un algorithme de programmation dynamique et obtenir une solution optimale ?
Sep 21, 2023 am 10:33 AM
Comment résoudre le problème du sac à dos en PHP en utilisant un algorithme de programmation dynamique et obtenir une solution optimale ?
Sep 21, 2023 am 10:33 AM
Comment résoudre le problème du sac à dos en PHP en utilisant un algorithme de programmation dynamique et obtenir une solution optimale ? Le problème du sac à dos est l’un des problèmes d’optimisation combinatoire classiques en informatique. Étant donné un ensemble d'articles et la capacité d'un sac à dos, la manière de sélectionner les articles à mettre dans le sac à dos afin de maximiser la valeur totale des articles dans le sac à dos est au cœur du problème du sac à dos qui doit être résolu. La programmation dynamique est l'une des méthodes courantes pour résoudre le problème du sac à dos. Il obtient finalement la solution optimale en divisant le problème en sous-problèmes et en enregistrant les solutions des sous-problèmes. Ci-dessous, nous expliquerons en détail comment utiliser l'algorithme de programmation dynamique en PHP
 Programmation dynamique de mémisation (1D, 2D et 3D) en Java
Aug 23, 2023 pm 02:13 PM
Programmation dynamique de mémisation (1D, 2D et 3D) en Java
Aug 23, 2023 pm 02:13 PM
La mémorisation est une technique basée sur la programmation dynamique utilisée pour améliorer les performances des algorithmes récursifs en garantissant qu'une méthode ne s'exécute pas plusieurs fois sur le même ensemble d'entrées, en enregistrant les résultats (stockés dans un tableau) pour les entrées fournies. La mémorisation peut être réalisée grâce à une approche descendante qui met en œuvre des méthodes récursives. Comprenons cette situation à travers un exemple de base de séquence de Fibonacci. Mémoïsation 1-D Nous considérerons un algorithme récursif avec un seul paramètre non constant (un seul paramètre change de valeur), cette méthode est donc appelée mémoïsation 1-D. Le code suivant permet de trouver le Nième (tous les termes jusqu'à N) dans la séquence de Fibonacci. Exemple publicintfibonacci(intn){ &nb
 Explication détaillée de l'algorithme de programmation dynamique en PHP
Jul 07, 2023 am 10:48 AM
Explication détaillée de l'algorithme de programmation dynamique en PHP
Jul 07, 2023 am 10:48 AM
Explication détaillée de l'algorithme de programmation dynamique en PHP La programmation dynamique (programmation dynamique) est une idée algorithmique pour résoudre des problèmes. Elle résout le problème global en décomposant le problème en sous-problèmes plus petits et en utilisant les résultats des sous-problèmes résolus. En PHP, les algorithmes de programmation dynamique peuvent être largement utilisés dans de nombreux domaines de l'informatique et des mathématiques, tels que les chemins les plus courts, la correspondance de chaînes et les problèmes de sac à dos. Cet article présentera en détail les principes de l'algorithme de programmation dynamique en PHP et fournira des exemples de code pour illustrer. 1. Calcul de programmation dynamique
 Algorithme de tri et de recherche de tableaux en PHP
Jun 23, 2023 am 09:45 AM
Algorithme de tri et de recherche de tableaux en PHP
Jun 23, 2023 am 09:45 AM
PHP est un langage de programmation très populaire qui prend en charge divers types de données et algorithmes, dont les algorithmes de tri de tableaux et de recherche sont des éléments fondamentaux et importants. Cet article présentera les algorithmes de tri et de recherche de tableaux couramment utilisés en PHP, ainsi que leurs scénarios d'application et leur analyse d'efficacité. 1. Tri de tableaux PHP propose une variété de méthodes de tri de tableaux, notamment le tri à bulles, le tri par insertion, le tri par sélection, le tri rapide, le tri par fusion, etc. Ce qui suit est une introduction et un exemple de code pour plusieurs algorithmes couramment utilisés : Tri à bulles (BubbleSort)





