Prouver que l'ensemble dominant d'un graphe est NP-complet

Un ensemble dominant d'un graphe est un problème NP-complet, qui est un sous-ensemble de sommets tel que chaque sommet ou sommet adjacent du sous-ensemble se trouve dans le sous-ensemble. La forme complète de NP est « polynôme non déterministe » qui vérifiera le problème en temps polynomial, ce qui signifie que nous pouvons vérifier en temps polynomial si la solution est correcte. Le temps polynomial a la meilleure complexité pour des codes comme la complexité du temps de recherche linéaire – n, recherche binaire – logn, tri par fusion - n(log)n etc. Les graphiques NP-complets fournissent une bonne solution dans un délai raisonnable. Cette application est utilisée dans des domaines tels que le contrôle de réseau, la création de topologie dans les laboratoires informatiques, les réseaux sociaux et l'informatique distribuée.

Comprenons et vérifions si un nœud a l'ensemble dominant d'un graphe NP complet.

On dit qu’un sommet se domine lui-même ainsi que chacun de ses voisins.

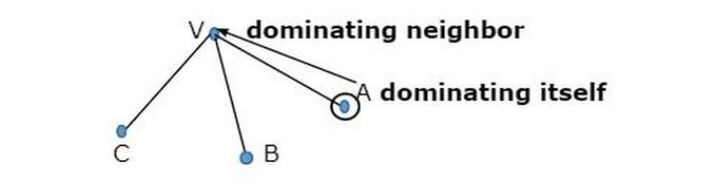
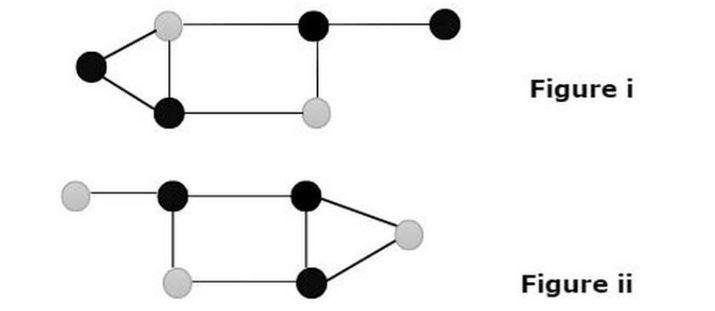
Nous voyons deux graphiques montrant les nœuds du graphique où la couleur grise domine dans la nature.

G = V, E

Paramètres

G est considéré comme un graphe, V est considéré comme un sommet et E est considéré comme une arête.

Étant donné un graphe G(V, E) et un entier k, déterminez si le graphe a un ensemble dominant de taille k. Une entrée spécifiée comme problème est considérée comme une instance du problème. Le graphe G(V, E) et l'entier k servent d'exemples du problème de l'ensemble dominant, qui demande si le graphe G peut avoir un ensemble dominant dans G. Puisque la définition du problème NP-complet est un problème à la fois NP et NP-difficile, prouver qu’un problème est NP-complet comporte deux composantes −

Dominator définit des problèmes NP-complets

S'il existe un problème NP Y qui se réduit à X en temps polynomial, alors X est un problème NP-complet. Les problèmes NP-complets sont tout aussi difficiles que les problèmes NP. Un problème est NP-Complet s’il fait à la fois partie d’un problème NP et d’un problème NP-Difficile. Les machines de Turing non déterministes peuvent résoudre des problèmes NP-complets en temps polynomial. Lorsqu'un problème est np-complet, il comporte à la fois des combinaisons np et np-difficiles.

Cela signifie que les problèmes avec les solutions np peuvent être vérifiés en temps polynomial.

De vrais exemples de NP complets ont des ensembles dominants tels que -

• Problème de prise de décision.

• Les graphismes sont cohérents.

Algorithme de recherche non déterministe

NP_search( key ) {
   arraylist[100];
   i = array_check(key);
   if(list[i]==key) {
      searching found at index i.
   } else {
      searching found at index i.
   }
}

Donc, la complexité temporelle totale de cet algorithme est O(1), mais nous ne savons pas quelle technique de recherche est la plus utile pour résoudre ce problème, c'est ce qu'on appelle un algorithme non déterministe.

Dominator défini dans des problèmes NP-difficiles

Un problème X est NP-difficile s'il existe un problème NP-complet Y qui se réduit au problème X en temps polynomial. Les problèmes NP-difficiles sont aussi difficiles que les problèmes NP-complets. Un problème NP-difficile n’appartient pas nécessairement à la catégorie NP.

Si chaque problème NP peut être résolu en temps polynomial, on l'appelle NP-Hard. Souvent, un problème spécifique est utilisé pour résoudre et réduire d’autres problèmes.

De vrais exemples de

NP-hard ont des ensembles dominants tels que -

• Cycle hamiltonien

• Problèmes d'optimisation

• Itinéraire le plus court

Conclusion

Nous avons appris le concept selon lequel l'ensemble dominant d'un graphe est NP-complet. Nous voyons à quel point les mathématiques discrètes sont un aspect important reliant ces problèmes, tels que les cycles de Hamilton, les chemins les plus courts, etc. En termes de programmation, les problèmes NP-complets sont une classe de problèmes dont les solutions sont difficiles à trouver mais dont les solutions peuvent être directement vérifiées en temps polynomial.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!