Comment utiliser l'algorithme de Kruskal en C++

Comment utiliser l'algorithme de Kruskal en C++
L'algorithme de Kruskal est un algorithme glouton couramment utilisé pour résoudre le problème de l'arbre couvrant minimum. En programmation en C++, nous pouvons comprendre et utiliser l'algorithme de Kruskal à travers des exemples de code simples.
L'idée de base de l'algorithme de Kruskal est de sélectionner en continu l'arête ayant le plus petit poids d'arête et qui ne forme pas de boucle tant que tous les sommets ne sont pas inclus dans l'arbre couvrant. Ci-dessous, nous présenterons étape par étape comment utiliser C++ pour implémenter l'algorithme de Kruskal.
Étape 1 : Préparation des données
Tout d'abord, nous devons préparer une structure de données graphique pour représenter le problème. En C++, les graphiques peuvent être représentés à l'aide de matrices de contiguïté ou de listes de contiguïté. Ici, nous choisissons d'utiliser des listes de contiguïté pour représenter des graphiques non orientés.
Les listes de contiguïté peuvent être implémentées en utilisant une combinaison de vecteurs et de listes chaînées. Nous définissons deux structures pour représenter les sommets et les arêtes du graphe.
// 图的顶点结构体
struct Vertex {
int id; // 顶点的唯一标识符
// ...
};
// 图的边结构体
struct Edge {
int start; // 边的起始顶点
int end; // 边的结束顶点
int weight; // 边的权重
// ...
};
// 定义一个无向图的类
class Graph {
public:
// 添加顶点和边的函数
void addVertex(Vertex v);
void addEdge(Edge e);
// ...
private:
// 保存顶点和边的数据结构
vector<Vertex> vertices;
list<Edge> edges;
// ...
};Étape 2 : Implémenter l'algorithme Kruskal
Après avoir préparé la structure des données du graphique, nous pouvons commencer à implémenter l'algorithme Kruskal. Tout d’abord, nous devons trier les bords du graphique de petit à grand en poids. Ensuite, nous utilisons Union-Find pour déterminer si les arêtes sélectionnées formeront un cycle. Enfin, nous ajoutons les arêtes sélectionnées à l'arbre couvrant minimum.
Ce qui suit est le code d'implémentation spécifique de l'algorithme Kruskal :
// 定义并查集结构体
struct UnionFind {
vector<int> parent;
// ...
};
// 初始化并查集
void initUnionFind(UnionFind& uf, int n) {
uf.parent.resize(n);
// ...
}
// 查找根节点
int findRoot(UnionFind& uf, int x) {
if (uf.parent[x] != x) {
uf.parent[x] = findRoot(uf, uf.parent[x]);
}
return uf.parent[x];
}
// 合并两个集合
void mergeSets(UnionFind& uf, int x, int y) {
int rootX = findRoot(uf, x);
int rootY = findRoot(uf, y);
if (rootX != rootY) {
uf.parent[rootX] = rootY;
}
}
// Kruskal算法主函数
list<Edge> kruskal(Graph& graph) {
list<Edge> minSpanningTree;
// 将图的边按照权重从小到大排序
graph.edges.sort([](const Edge& e1, const Edge& e2) {
return e1.weight < e2.weight;
});
int numVertices = graph.vertices.size();
UnionFind uf;
initUnionFind(uf, numVertices);
for (const Edge& edge : graph.edges) {
int startRoot = findRoot(uf, edge.start);
int endRoot = findRoot(uf, edge.end);
// 如果两个顶点不在同一个集合中,则添加该边到最小生成树中
if (startRoot != endRoot) {
minSpanningTree.push_back(edge);
mergeSets(uf, startRoot, endRoot);
}
}
return minSpanningTree;
}Étape 3 : tester le code
Écrivez une fonction de test, créez un graphique et appelez l'algorithme Kruskal, et affichez l'arbre couvrant minimum :
void testKruskal() {
Graph graph;
// 添加顶点和边
// ...
list<Edge> minSpanningTree = kruskal(graph);
// 输出最小生成树
for (const Edge& edge : minSpanningTree) {
cout << edge.start << " -> " << edge.end << ", weight: " << edge.weight << endl;
}
}
int main() {
testKruskal();
return 0;
}Ce qui précède est l'implémentation de l'algorithme Kruskal en utilisant C++ Un exemple simple. Grâce à cet exemple, vous pouvez mieux comprendre et utiliser l'algorithme de Kruskal pour résoudre le problème de l'arbre couvrant minimum.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment utiliser C++ pour implémenter la fonction de tâche planifiée des systèmes embarqués
Aug 27, 2023 pm 12:05 PM
Comment utiliser C++ pour implémenter la fonction de tâche planifiée des systèmes embarqués
Aug 27, 2023 pm 12:05 PM
Comment utiliser C++ pour implémenter la fonction de tâche planifiée des systèmes embarqués Les systèmes embarqués doivent souvent implémenter la fonction de tâche planifiée, c'est-à-dire exécuter certaines tâches dans un intervalle de temps spécifique. En tant que langage de programmation puissant, C++ nous fournit de nombreux outils et bibliothèques pour réaliser de telles fonctions. Cet article explique comment utiliser le langage de programmation C++ pour implémenter des fonctions de tâches planifiées dans les systèmes embarqués et fournit quelques exemples de code. Utilisation des interruptions de minuterie Dans les systèmes embarqués, nous pouvons utiliser des interruptions de minuterie pour implémenter des fonctions de tâches planifiées. En réglant la minuterie
 Comment utiliser l'algorithme de Kruskal en C++
Sep 19, 2023 pm 04:10 PM
Comment utiliser l'algorithme de Kruskal en C++
Sep 19, 2023 pm 04:10 PM
Comment utiliser l'algorithme de Kruskal en C++ L'algorithme de Kruskal est un algorithme glouton couramment utilisé pour résoudre le problème de l'arbre couvrant minimum. En programmation en C++, nous pouvons comprendre et utiliser l'algorithme de Kruskal à travers des exemples de code simples. L'idée de base de l'algorithme de Kruskal est de sélectionner en continu l'arête ayant le plus petit poids d'arête et qui ne forme pas de boucle tant que tous les sommets ne sont pas inclus dans l'arbre couvrant. Ci-dessous, nous présenterons étape par étape comment utiliser C++ pour implémenter l'algorithme de Kruskal. Première étape : préparation des données Tout d'abord, je
 Pourquoi l'algorithme d'arbre couvrant minimum de Prim et Kruskal échoue-t-il dans les graphes orientés ?
Sep 02, 2023 pm 05:29 PM
Pourquoi l'algorithme d'arbre couvrant minimum de Prim et Kruskal échoue-t-il dans les graphes orientés ?
Sep 02, 2023 pm 05:29 PM
La méthode de Prim et l'algorithme de Kruskal sont deux méthodes courantes pour localiser le MST (minimum spanning tree) dans des graphiques non orientés. Cependant, ces techniques ne peuvent pas générer un MST correct pour les graphes orientés. En effet, les graphes orientés ne correspondent pas aux hypothèses et méthodes de base utilisées par les algorithmes de Prim et Kruskal. L'algorithme de Prim Tout d'abord, il y a l'algorithme de Prim, qui consiste à ajouter des arêtes à un arbre couvrant minimum en expansion de manière gourmande jusqu'à ce que tous les sommets soient couverts. Les sommets à l'intérieur du MST sont connectés aux sommets à l'extérieur du MST via l'arête ayant le poids le plus faible. Puisque toutes les arêtes d’un graphe non orienté peuvent se déplacer dans n’importe quelle direction, le chemin le plus court entre le MST et les sommets externes est facile à trouver. Cependant, dans un graphe orienté, les arêtes pointent toujours dans une direction et il peut ne pas y avoir de ligne droite.
 Algorithme de récupération à grande vitesse et son application en PHP
Jun 22, 2023 pm 05:31 PM
Algorithme de récupération à grande vitesse et son application en PHP
Jun 22, 2023 pm 05:31 PM
En tant que langage de programmation côté serveur populaire, PHP joue un rôle indispensable dans le développement d'applications Web. Dans le développement réel, nous devons souvent effectuer des opérations telles que la récupération et la recherche sur de grandes quantités de données. À l'heure actuelle, les algorithmes de récupération à grande vitesse sont devenus une direction très importante. Cet article présentera les algorithmes de récupération à grande vitesse couramment utilisés en PHP et leurs applications. 1. Présentation Dans la structure des données, la récupération fait référence à la recherche d'enregistrements de données avec des conditions spécifiées dans la collecte de données. Les méthodes de récupération courantes incluent la recherche linéaire, la recherche binaire, la recherche par hachage, etc. recherche linéaire
 Comment implémenter des systèmes de conduite autonome et de transport intelligents en C++ ?
Aug 26, 2023 am 08:58 AM
Comment implémenter des systèmes de conduite autonome et de transport intelligents en C++ ?
Aug 26, 2023 am 08:58 AM
Comment implémenter des systèmes de conduite autonome et de transport intelligents en C++ ? La conduite autonome et les systèmes de transport intelligents sont actuellement des sujets brûlants dans le domaine de l'intelligence artificielle, et leurs domaines d'application impliquent de nombreux aspects tels que les transports, la protection de la sécurité et l'urbanisme. Cet article explorera comment utiliser le langage de programmation C++ pour mettre en œuvre des systèmes de conduite autonome et de transport intelligents, et fournira des exemples de code pertinents. Comprendre les principes de base de la conduite autonome et des systèmes de transport intelligents. Les systèmes de conduite autonome font référence à une technologie qui utilise des ordinateurs, des capteurs et d'autres équipements pour naviguer et conduire des véhicules de manière autonome. il faut qu'il soit perçu en temps réel
 Comment utiliser C++ pour implémenter un système embarqué avec des fonctionnalités temps réel
Aug 25, 2023 pm 03:18 PM
Comment utiliser C++ pour implémenter un système embarqué avec des fonctionnalités temps réel
Aug 25, 2023 pm 03:18 PM
Comment utiliser C++ pour implémenter un système embarqué avec des fonctions temps réel Introduction : Avec le développement continu de la technologie, les systèmes embarqués ont été largement utilisés dans divers domaines. La fonctionnalité en temps réel est une fonctionnalité cruciale dans les systèmes embarqués, en particulier dans les scénarios nécessitant une réponse immédiate à des événements externes. Cet article présentera comment utiliser le langage C++ pour implémenter un système embarqué avec des fonctions temps réel et donnera des exemples de code. Système d'exploitation en temps réel (RTOS) Le système d'exploitation en temps réel (RTOS) est la clé pour obtenir une fonctionnalité en temps réel. RTOS a une planification des tâches,
 Algorithme d'arbre couvrant minimum de Kruskal - Algorithme gourmand en C++
Aug 28, 2023 pm 03:05 PM
Algorithme d'arbre couvrant minimum de Kruskal - Algorithme gourmand en C++
Aug 28, 2023 pm 03:05 PM
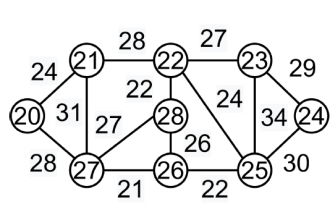
Un arbre couvrant est un sous-graphe d'un graphe orienté non orienté qui relie tous les sommets. Il peut y avoir plusieurs arbres couvrants dans un graphique. L'arbre couvrant minimum (MST) sur chaque graphique a un poids identique ou inférieur à celui de tous les autres arbres couvrant. Des poids sont attribués aux arêtes du spanning tree, et la somme correspond au poids attribué à chaque arête. Puisque V est le nombre de sommets dans le graphe, le nombre d’arêtes de l’arbre couvrant minimum est (V-1), où V est le nombre d’arêtes. Utilisez l'algorithme de Kruskal pour trouver l'arbre couvrant minimum. Toutes les arêtes doivent être disposées dans un ordre non décroissant par poids. Choisissez le plus petit côté. Si aucune boucle n'est formée, le bord est inclus. L'étape 2 doit être effectuée jusqu'à ce que l'arbre couvrant ait des bords (V-1). Dans ce cas, on nous dit d’utiliser l’approche gourmande. L’option gourmande est de choisir le bord avec le plus petit poids. Par exemple : l'arbre couvrant minimum de ce graphique est (9-1)=8
 Comment implémenter l'algorithme Kruskal en Java
May 11, 2023 pm 10:19 PM
Comment implémenter l'algorithme Kruskal en Java
May 11, 2023 pm 10:19 PM
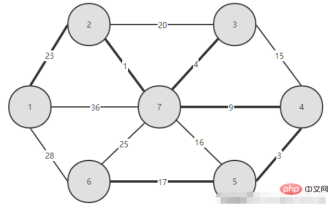
Présentation d'un autre algorithme pour construire un arbre couvrant minimum, l'algorithme de Kruskal : Soit le graphe G = (V, E) un graphe pondéré connecté non orienté, V = {1, 2,...n} soit l'arbre couvrant minimum T ; = (V, TE), l'état initial de l'arbre est un graphe non connecté avec seulement n nœuds et aucune arête T = (V, {}). L'algorithme de Kruskal traite ces n nœuds comme n branches connectées isolées. Il trie d'abord toutes les arêtes en fonction de leurs poids de petit à grand, puis si le nombre d'arêtes à sélectionner dans T est inférieur à n-1, il effectue une sélection gloutonne comme celle-ci : sélectionne l'arête (i, j) avec le plus petit poids dans l'ensemble d'arêtes E ), si l'ajout d'arête (i, j) à l'ensemble TE ne produit pas de cycle, alors ajoutez l'arête (i, j) à l'ensemble d'arêtes TE, c'est-à-dire utilisez l'arête (i , j) pour fusionner les deux branches en une seule






