Trouvez le chemin le plus court entre deux nœuds à l'aide de l'algorithme Floyd-Warshal

C++ a une macro, qui est définie comme un morceau de code ou une valeur attendue, et elle sera réutilisée chaque fois que l'utilisateur en aura besoin. L'algorithme de Floyd-Walshall est le processus permettant de trouver le chemin le plus court entre toutes les paires de sommets dans un graphe pondéré donné. L'algorithme suit une approche de programmation dynamique pour trouver le graphique de poids minimum.

Comprenons la signification de l'algorithme de Freud-Walshire à travers des diagrammes -

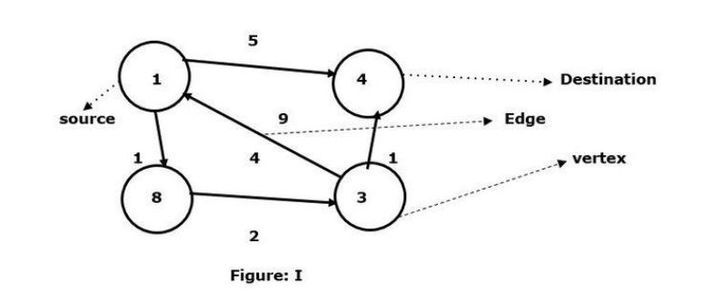
Avec le sommet 1 comme source et le sommet 4 comme destination, trouvez le chemin le plus court entre eux.

Nous avons vu qu'il existe deux chemins qui peuvent être connectés au sommet cible 4.

• 1 -> 4 – Le bord a un poids de 5

• 1 -> 8 -> 3 -> 4 – Le poids du bord (1+2+1) est de 4.

Dans le graphique I donné, nous voyons l'arête minimale reliant deux sommets. Voici donc le chemin du sommet 8 au sommet 3 reliant le sommet 1 au sommet 4 et l'arête est 4. D’un autre côté, il existe une arête dirigée du sommet 1 au sommet 4, et le poids de l’arête est 5.

Maintenant, nous comparons deux poids, à savoir 4 et 5. Par conséquent, voici 4 est le poids minimum du graphique calculé selon l'algorithme de Floyd Warshall.

Dans cet article, nous utiliserons l'algorithme de Floyd Warshall pour trouver le chemin le plus court entre deux nœuds donnés.

Grammaire

La syntaxe suivante est utilisée dans le programme -

data_type[][] array_name;

Paramètres

data_type[][] - Le type de données mentionné par l'utilisateur. Le premier tableau représente les lignes et le deuxième tableau représente les colonnes. Cela représente donc un tableau à deux dimensions.

array_name - Le nom donné au tableau.

Algorithme

• Nous allons démarrer le programme avec le fichier d'en-tête 'iostream' et définir l'emplacement de la macro comme 'INF' (infini) car plus tard, il satisfera la matrice de tableau 2D et l'instruction if-else.

• Ensuite, nous créons une définition de fonction globale appelée 'printPath' et acceptons trois paramètres, 'parent[]', 'i' et 'j' pour vérifier que le chemin existe.

• Ensuite, nous démarrons la fonction principale et stockons la valeur ‘4’ dans la variable ‘V’, qui représente le nombre de sommets. Deuxièmement, stockez la valeur sous la forme d’une matrice de contiguïté dans la variable ‘dist[V][V]’. Comme nous le savons, dist[i][j] représente une matrice 2D, qui définit le poids de l'arête de 'i' à 'j', en stockant la matrice de contiguïté.

• Ensuite, nous initialisons un tableau 2D pour la variable ‘parent’, de taille [V][V].

Dans cette variable, nous utilisons pour afficher chaque paire de sommets 'i' et 'j' par rapport à 'parent[i][j]'< /b>.

• En utilisant deux boucles for imbriquées, nous trouverons le chemin le plus court. La première boucle for parcourt les lignes de la matrice. Ensuite, parcourez les colonnes de la matrice à travers la deuxième boucle for, puis nous vérifierons la condition suivante en utilisant l'instruction if-else -

• Si (dist[i][j] != INF && i != j) { La traduction chinoise de parent[i][j] = i;}

  est : parent[i][j] = i;}

  Dans l'instruction if, nous utilisons l'opérateur 'and' (&&) pour exprimer deux conditions si les deux conditions sont remplies, alors 'i' sera stocké dans 'parent[i][j]' , vérifiant ainsi que. le chemin existe.

• Autres{ La traduction chinoise de parent[i][j] = -1;}

  est : parent[i][j] = -1;}

  Dans l'instruction else, nous initialisons "-1" à "parent[i][j]" pour vérifier que le chemin n'existe pas.

• Maintenant, nous commençons avec trois boucles for imbriquées et appliquons k sommets compris entre 0 et V-1, avec l'aide de cette plage, notre distance et notre chemin les plus courts seront mis à jour. Dans la troisième boucle imbriquée, nous utilisons la condition suivante comme

if (dist[i][j] < dist[i][k] + dist[k][j]){
   dist[i][j] = dist[i][k] + dist[k][j]; 
   parent[i][j] = parent[k][j];	
}

Ici, K met à jour les parties de ligne et de colonne de la matrice de tableau 2D, qui vérifie le chemin et la distance les plus courts récemment mis à jour.

• Ensuite, nous imprimons la distance et le chemin les plus courts de toutes les paires de sommets en donnant les conditions suivantes

• En utilisant deux boucles for imbriquées, nous imprimons la distance et le chemin les plus courts.

• En utilisant l'instruction if sous la deuxième boucle for, nous vérifierons si dist[i][j] est égal à l'infini. S'il s'avère être l'infini, imprimez "INF", sinon imprimez le chemin le plus court.

• Enfin, nous appelons la fonction appelée 'printPath()' en passant trois paramètres (parent[i], i et j.

Exemple

Dans ce programme, nous utiliserons l'algorithme Floyd Warshall pour calculer le chemin le plus court entre deux nœuds quelconques.

#include <iostream> 
using namespace std; 
#define INF 1000000000 // Infinity

void printPath(int parent[], int i, int j) {
   if (i == j) 
      cout << i << " "; 
   else if (parent[j] == -1) 
     cout << "No path exists"; 
   else
   { 
      printPath(parent, i, parent[j]); 
      cout << j << " "; 
   }
} 

int main() 
{
   int V = 4; 
   // V represent number of vertices
   int dist[V][V] = {{0, 2, INF, 4}, 
      {6, 0, 5, 3}, 
      {INF, 10, 0, 1}, 
      {7, 9, 8, 0}}; 
   // Represent the graph using adjacency matrix

   // Apply the Floyd Warshall algorithm to find the shortest paths
   int parent[V][V];
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      {
         if (dist[i][j] != INF && i != j)
         parent[i][j] = i;
         else
         parent[i][j] = -1;
      }
   }
   // update the path and distance using the k vertex range from 0 to V-1.
   for (int k = 0; k < V; k++) 
   { 
      for (int i = 0; i < V; i++) 
      { 
         for (int j = 0; j < V; j++) 
         { 
            if (dist[i][j] > dist[i][k] + dist[k][j]) 
            {
               dist[i][j] = dist[i][k] + dist[k][j];
               parent[i][j] = parent[k][j];	
            }
         }
      }
   }

   // Print shortest distances and paths between all pairs of vertices
   for (int i = 0; i < V; i++) 
   { 
      for (int j = 0; j < V; j++) 
      { 
         cout << "The Shortest distance between " << i << " and " << j << " is ";
         if (dist[i][j] == INF) 
            cout << "INF "; 
         else
            cout << dist[i][j] << " ";

         cout << "and the shortest path is:- ";
         printPath(parent[i], i, j);
         cout << endl;
      } 
   } 

   return 0; 
}

输出

The Shortest distance between 0 and 0 is 0 and the shortest path is:- 0 
The Shortest distance between 0 and 1 is 2 and the shortest path is:- 0 1 
The Shortest distance between 0 and 2 is 7 and the shortest path is:- 0 1 2 
The Shortest distance between 0 and 3 is 4 and the shortest path is:- 0 3 
The Shortest distance between 1 and 0 is 6 and the shortest path is:- 1 0 
The Shortest distance between 1 and 1 is 0 and the shortest path is:- 1 
The Shortest distance between 1 and 2 is 5 and the shortest path is:- 1 2 
The Shortest distance between 1 and 3 is 3 and the shortest path is:- 1 3 
The Shortest distance between 2 and 0 is 8 and the shortest path is:- 2 3 0 
The Shortest distance between 2 and 1 is 10 and the shortest path is:- 2 1 
The Shortest distance between 2 and 2 is 0 and the shortest path is:- 2 
The Shortest distance between 2 and 3 is 1 and the shortest path is:- 2 3 
The Shortest distance between 3 and 0 is 7 and the shortest path is:- 3 0 
The Shortest distance between 3 and 1 is 9 and the shortest path is:- 3 1 
The Shortest distance between 3 and 2 is 8 and the shortest path is:- 3 2 
The Shortest distance between 3 and 3 is 0 and the shortest path is:- 3 

结论

我们学习了使用Floyd Warshall算法找到任意两个节点之间的最短路径的概念。我们使用邻接矩阵作为程序的输入，通过它我们找到了最短路径和距离。此外，为了更新路径和距离，我们使用了k个顶点来更新行和列。在我们的日常生活中，我们在谷歌地图上搜索最短路线或路径，从一个起点到目的地。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!