nombre heptagonal
Un nombre heptagonal est un nombre qui peut être représenté comme un heptagone. Un nombre heptagonal peut être représenté comme une combinaison de couches successives d'heptagone (polygone à 7 côtés expliqué avec les figures ci-dessous).
 Le premier nombre heptagonal est 1. Il peut donc être représenté par un petit point.
Le premier nombre heptagonal est 1. Il peut donc être représenté par un petit point.
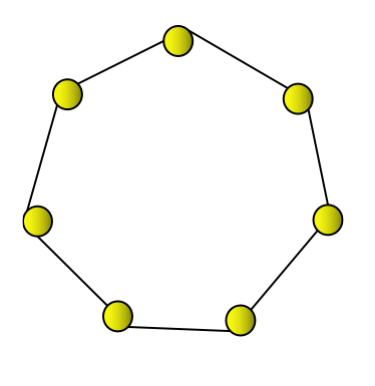 Le deuxième nombre heptagonal est 7, qui peut être représenté par un heptagone.
Le deuxième nombre heptagonal est 7, qui peut être représenté par un heptagone.
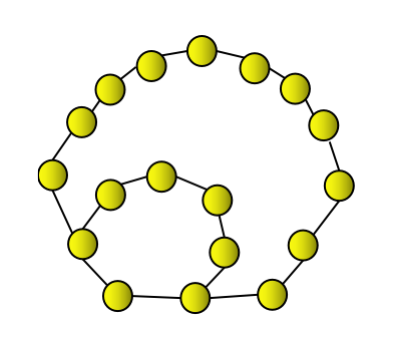 Le troisième nombre d'heptagone est 18, qui peut être représenté par un heptagone et combiné avec une couche d'heptagone continue.
Le troisième nombre d'heptagone est 18, qui peut être représenté par un heptagone et combiné avec une couche d'heptagone continue.
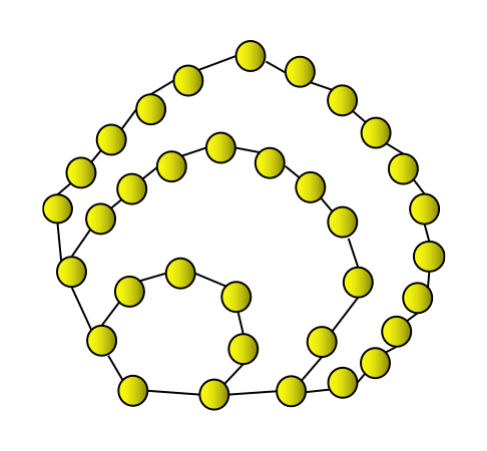 Le quatrième nombre heptagonal est 34. Il peut être représenté de la manière indiquée ci-dessus comme un heptagone plus deux couches consécutives d'heptagones, ce qui donne 34.
Le quatrième nombre heptagonal est 34. Il peut être représenté de la manière indiquée ci-dessus comme un heptagone plus deux couches consécutives d'heptagones, ce qui donne 34. Des concepts similaires seront utilisés pour d’autres nombres heptagonaux. Suivant la même logique, les premiers nombres heptagonaux sont
1, 7, 18, 34, 55, 81, 112, 148, 189, 235, 286, 342, 403…
Dans ce problème, notre tâche est de donner n'importe quel nombre positif N en entrée et d'imprimer le Nième nombre d'heptagone en sortie.Par exemple,
ENTRÉE : N=6
Sortie : 81
ENTRÉE : N=9
Sortie : 189
Regardons maintenant l'algorithme que nous utiliserons pour résoudre ce problème.Algorithme
Pour résoudre ce problème, nous devons voir le modèle suivi en calculant le nième nombre heptagonal. Le nième nombre heptagonal peut être exprimé par −
$$Heptagonal_{n}:=:frac{n}{2}(5n:-:3)$$
Si nous regardons attentivement cette expression, chaque nombre heptagonal a la forme suivante
$frac{n}{2}(5n:-:3)$, où n représente le nombre de nombres heptagonaux.
Comprenons-le mieux avec un exemple.
Pour n=1, $frac{1}{2}(5:times:1:-:3)$= 1, qui est le premier nombre heptagonal.
Pour n=2, $frac{2}{2}(5:times:2:-:3)$= 7, qui est le deuxième nombre heptagonal.
Quand n=3, $frac{3}{2}(5:times:3:-:3)$= 18, qui est le troisième nombre heptagonal.
Maintenant, vérifions le cas de n=8. Le résultat obtenu par $frac{8}{2}(5:times:8:-:3)$ est 148, qui est en fait le huitième nombre heptagonal dans la séquence de nombres heptagonaux.
Puisque nous pouvons obtenir n'importe quel nième nombre heptagonal en utilisant l'expression ci-dessus, dans notre méthode, nous utiliserons cette expression pour calculer le nième nombre heptagonal, où n peut être n'importe quel nombre positif.
Méthode
Nous vous expliquerons dans les étapes suivantes :
- Prenez n'importe quel nombre positif N en entrée et calculez la valeur heptagonale correspondante N.
- Initialisez une fonction pour calculer le Nième nombre d'heptagone.
- Utilisez l'expression mentionnée dans la section algorithme, c'est-à-dire $frac{N}{2}(5N:-:3)$, pour calculer le Nième nombre d'heptagone et le stocker dans une variable arbitraire.
- Renvoie notre variable stockée qui sera la valeur du Nième nombre heptagonal correspondant à toute valeur positive N.
Remarque - Nous utiliserons le type de données à virgule flottante au lieu du type de données entier pour éviter toute erreur due aux valeurs décimales lors du calcul du Nième nombre heptagonal à l'aide de la formule ci-dessus. La traduction chinoise de
Exempleest :
ExempleImplémentez cette méthode en C++ −
#include <bits/stdc++.h>
#include <iostream>
using namespace std;
//function to calculate nth heptagonal number using formula n/2(5n-3)
float heptagonal(float N){
float ans= (N/2)*((5*N) - 3); //to store nth heptagonal number
return ans;
}
int main(){
float N=5; //input
float a=heptagonal(N); //store the answer in a variable
N=13;
float b=heptagonal(N);
cout<<a<<endl<<b<<endl; //print the answer
return 0;
}
55
403
Copier après la connexion
55 403
Complexité temporelle : O(1), car cela ne prend que un temps constant.
Complexité spatiale : O(1), car aucun espace supplémentaire n'est utilisé.
ConclusionNous avons essayé d'apprendre le concept des nombres heptagonaux et la formule de calcul du nième nombre heptagonal que nous avons utilisée dans la méthode.
J'espère que vous avez trouvé cet article utile pour apprendre le concept d'impression du nième nombre heptagonal saisi par n'importe quel utilisateur.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1359
1359
 52
52
 L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L'IA bouleverse la recherche mathématique ! Le lauréat de la médaille Fields et mathématicien sino-américain a dirigé 11 articles les mieux classés | Aimé par Terence Tao
Apr 09, 2024 am 11:52 AM
L’IA change effectivement les mathématiques. Récemment, Tao Zhexuan, qui a prêté une attention particulière à cette question, a transmis le dernier numéro du « Bulletin de l'American Mathematical Society » (Bulletin de l'American Mathematical Society). En se concentrant sur le thème « Les machines changeront-elles les mathématiques ? », de nombreux mathématiciens ont exprimé leurs opinions. L'ensemble du processus a été plein d'étincelles, intense et passionnant. L'auteur dispose d'une équipe solide, comprenant Akshay Venkatesh, lauréat de la médaille Fields, le mathématicien chinois Zheng Lejun, l'informaticien de l'Université de New York Ernest Davis et de nombreux autres universitaires bien connus du secteur. Le monde de l’IA a radicalement changé. Vous savez, bon nombre de ces articles ont été soumis il y a un an.
 Supprimez les valeurs en double du tableau PHP à l'aide d'expressions régulières
Apr 26, 2024 pm 04:33 PM
Supprimez les valeurs en double du tableau PHP à l'aide d'expressions régulières
Apr 26, 2024 pm 04:33 PM
Comment supprimer les valeurs en double du tableau PHP à l'aide d'expressions régulières : utilisez l'expression régulière /(.*)(.+)/i pour faire correspondre et remplacer les doublons. Parcourez les éléments du tableau et vérifiez les correspondances à l'aide de preg_match. S'il y a une correspondance, ignorez la valeur ; sinon, ajoutez-la à un nouveau tableau sans valeurs en double.
 L'algorithme CVM révolutionnaire résout plus de 40 ans de problèmes de comptage ! Un informaticien lance une pièce de monnaie pour trouver le mot unique pour « Hamlet »
Jun 07, 2024 pm 03:44 PM
L'algorithme CVM révolutionnaire résout plus de 40 ans de problèmes de comptage ! Un informaticien lance une pièce de monnaie pour trouver le mot unique pour « Hamlet »
Jun 07, 2024 pm 03:44 PM
Compter semble simple, mais en pratique, c'est très difficile. Imaginez que vous êtes transporté dans une forêt tropicale vierge pour effectuer un recensement de la faune. Chaque fois que vous voyez un animal, prenez une photo. Les appareils photo numériques enregistrent uniquement le nombre total d'animaux suivis, mais vous êtes intéressé par le nombre d'animaux uniques, mais il n'y a pas de statistiques. Alors, quelle est la meilleure façon d’accéder à cette population animale unique ? À ce stade, vous devez dire : commencez à compter maintenant et comparez enfin chaque nouvelle espèce de la photo à la liste. Cependant, cette méthode de comptage courante n'est parfois pas adaptée aux informations pouvant atteindre des milliards d'entrées. Des informaticiens de l'Institut indien de statistique, UNL, et de l'Université nationale de Singapour ont proposé un nouvel algorithme : le CVM. Il peut approximer le calcul de différents éléments dans une longue liste.
 MLP a été tué du jour au lendemain ! Le MIT Caltech et d'autres KAN révolutionnaires battent des records et découvrent des théorèmes mathématiques qui écrasent DeepMind
May 06, 2024 pm 03:10 PM
MLP a été tué du jour au lendemain ! Le MIT Caltech et d'autres KAN révolutionnaires battent des records et découvrent des théorèmes mathématiques qui écrasent DeepMind
May 06, 2024 pm 03:10 PM
Du jour au lendemain, le paradigme de l’apprentissage automatique est sur le point de changer ! Aujourd’hui, l’infrastructure qui domine le domaine de l’apprentissage profond est le perceptron multicouche (MLP), qui place des fonctions d’activation sur les neurones. Alors, au-delà de cela, y a-t-il de nouvelles routes que nous pouvons emprunter ? Aujourd'hui encore, des équipes du MIT, de Caltech, de la Northeastern University et d'autres institutions ont publié une nouvelle structure de réseau neuronal : Kolmogorov-Arnold Networks (KAN). Les chercheurs ont apporté une modification simple au MLP en déplaçant la fonction d’activation apprenable des nœuds (neurones) vers les bords (poids) ! Adresse papier : https://arxiv.org/pdf/2404.19756 Ce changement semble à première vue sans fondement
 A quoi sert la programmation et à quoi sert de l'apprendre ?
Apr 28, 2024 pm 01:34 PM
A quoi sert la programmation et à quoi sert de l'apprendre ?
Apr 28, 2024 pm 01:34 PM
1. La programmation peut être utilisée pour développer divers logiciels et applications, notamment des sites Web, des applications mobiles, des jeux et des outils d'analyse de données. Ses domaines d'application sont très larges, couvrant presque tous les secteurs, notamment la recherche scientifique, la santé, la finance, l'éducation, le divertissement, etc. 2. L'apprentissage de la programmation peut nous aider à améliorer nos compétences en résolution de problèmes et nos capacités de réflexion logique. Lors de la programmation, nous devons analyser et comprendre les problèmes, trouver des solutions et les traduire en code. Cette façon de penser peut cultiver nos capacités analytiques et abstraites et améliorer notre capacité à résoudre des problèmes pratiques.
 Créez des applications basées sur un navigateur avec Golang
Apr 08, 2024 am 09:24 AM
Créez des applications basées sur un navigateur avec Golang
Apr 08, 2024 am 09:24 AM
Créez des applications basées sur un navigateur avec Golang Golang se combine avec JavaScript pour créer des expériences frontales dynamiques. Installez Golang : visitez https://golang.org/doc/install. Configurez un projet Golang : créez un fichier appelé main.go. Utilisation de GorillaWebToolkit : ajoutez le code GorillaWebToolkit pour gérer les requêtes HTTP. Créer un modèle HTML : créez index.html dans le sous-répertoire des modèles, qui est le modèle principal.
 La clé du codage : libérer la puissance de Python pour les débutants
Oct 11, 2024 pm 12:17 PM
La clé du codage : libérer la puissance de Python pour les débutants
Oct 11, 2024 pm 12:17 PM
Python est un langage d'introduction à la programmation idéal pour les débutants grâce à sa facilité d'apprentissage et ses fonctionnalités puissantes. Ses bases incluent : Variables : utilisées pour stocker des données (nombres, chaînes, listes, etc.). Type de données : Définit le type de données dans la variable (entier, virgule flottante, etc.). Opérateurs : utilisés pour les opérations mathématiques et les comparaisons. Flux de contrôle : contrôlez le flux d'exécution du code (instructions conditionnelles, boucles).
 Résolution de problèmes avec Python : débloquez des solutions puissantes en tant que codeur débutant
Oct 11, 2024 pm 08:58 PM
Résolution de problèmes avec Python : débloquez des solutions puissantes en tant que codeur débutant
Oct 11, 2024 pm 08:58 PM
Python permet aux débutants de résoudre des problèmes. Sa syntaxe conviviale, sa bibliothèque complète et ses fonctionnalités telles que les variables, les instructions conditionnelles et les boucles permettent un développement de code efficace. De la gestion des données au contrôle du flux du programme et à l'exécution de tâches répétitives, Python fournit




