Comment calculer les résidus studentisés en Python ?
Sep 24, 2023 pm 06:45 PMLes résidus étudiés sont souvent utilisés dans l'analyse de régression pour identifier les valeurs aberrantes potentielles dans les données. Les valeurs aberrantes sont des points qui diffèrent considérablement de la tendance globale des données et peuvent avoir un impact significatif sur le modèle ajusté. En identifiant et en analysant les valeurs aberrantes, vous pouvez mieux comprendre les modèles sous-jacents de vos données et améliorer la précision de vos modèles. Dans cet article, nous examinerons de plus près les résidus étudiants et comment les implémenter en python.
Qu’est-ce que le résidu étudiant ?
Le terme « résidus studentisés » fait référence à une classe spécifique de résidus dont l'écart type est divisé par l'estimation. Les résidus de l'analyse de régression décrivent la différence entre la valeur observée de la variable de réponse et sa valeur attendue générée par le modèle. Pour détecter les valeurs aberrantes dans les données susceptibles d'affecter de manière significative le modèle ajusté, des résidus étudiés ont été utilisés.
La formule suivante est couramment utilisée pour calculer les résidus studentisés -
studentized residual = residual / (standard deviation of residuals * (1 - hii)^(1/2))
Où « résiduel » fait référence à la différence entre la valeur de réponse observée et la valeur de réponse attendue, « écart type résiduel » fait référence à l'estimation de l'écart type résiduel et « hii » fait référence au facteur de levier pour chaque point de données.
Calculer les résidus studentisés à l'aide de Python
Le package statsmodels peut être utilisé pour calculer les résidus étudiants en Python. À titre d'illustration, considérons ce qui suit :
Grammaire
OLSResults.outlier_test()
Où OLSResults fait référence au modèle linéaire ajusté à l'aide de la méthode ols() de statsmodels.
df = pd.DataFrame({'rating': [95, 82, 92, 90, 97, 85, 80, 70, 82, 83],
'points': [22, 25, 17, 19, 26, 24, 9, 19, 11, 16]})
model = ols('rating ~ points', data=df).fit()
stud_res = model.outlier_test()
Où « note » et « score » font référence à une régression linéaire simple.
Algorithme
Importez numpy, pandas, API Statsmodel.
Créez un ensemble de données.
Effectuez un modèle de régression linéaire simple sur l'ensemble de données.
Calculez les résidus studentisés.
Imprimez les résidus studentisés.
Exemple
Voici une démonstration de l'utilisation de la bibliothèque scikit-posthocs pour exécuter les tests de Dunn -
#import necessary packages and functions
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
#create dataset
df = pd.DataFrame({'rating': [95, 82, 92, 90, 97, 85, 80, 70, 82, 83], 'points': [22, 25, 17, 19, 26, 24, 9, 19, 11, 16]})
Créez ensuite un modèle de régression linéaire en utilisant la classe OLS statsmodels -
#fit simple linear regression model
model = ols('rating ~ points', data=df).fit()
En utilisant la méthode outlier test(), les résidus studentisés pour chaque observation de l'ensemble de données peuvent être générés dans un DataFrame -
#calculate studentized residuals stud_res = model.outlier_test() #display studentized residuals print(stud_res)
Sortie
student_resid unadj_p bonf(p) 0 1.048218 0.329376 1.000000 1 -1.018535 0.342328 1.000000 2 0.994962 0.352896 1.000000 3 0.548454 0.600426 1.000000 4 1.125756 0.297380 1.000000 5 -0.465472 0.655728 1.000000 6 -0.029670 0.977158 1.000000 7 -2.940743 0.021690 0.216903 8 0.100759 0.922567 1.000000 9 -0.134123 0.897080 1.000000
Nous pouvons également tracer rapidement les valeurs prédictives par rapport aux résidus studentisés -
Grammaire
x = df['points']
y = stud_res['student_resid']
plt.scatter(x, y)
plt.axhline(y=0, color='black', linestyle='--')
plt.xlabel('Points')
plt.ylabel('Studentized Residuals')
Ici, nous utiliserons la bibliothèque matpotlib pour dessiner le graphique avec color = 'black' et lifestyle = '--'
Algorithme
Importer la bibliothèque pyplot de matplotlib
Définir les valeurs prédictives
Définir le résidu studentisé
Créez un nuage de points de prédicteurs par rapport aux résidus étudiantisés
Exemple
import matplotlib.pyplot as plt
#define predictor variable values and studentized residuals
x = df['points']
y = stud_res['student_resid']
#create scatterplot of predictor variable vs. studentized residuals
plt.scatter(x, y)
plt.axhline(y=0, color='black', linestyle='--')
plt.xlabel('Points')
plt.ylabel('Studentized Residuals')
Sortie
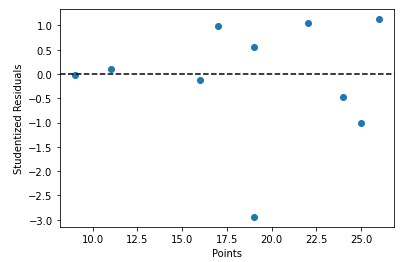
Conclusion
Identifier et évaluer les éventuelles valeurs aberrantes des données. L'examen des résidus étudiés vous permet de trouver les points qui s'écartent considérablement de la tendance globale des données et d'explorer pourquoi ils affectent le modèle ajusté. Identifier les observations significatives Les résidus studentisés peuvent être utilisés pour découvrir et évaluer des données influentes qui ont un impact significatif sur le modèle ajusté. Recherchez des emplacements à fort effet de levier. Les résidus studentisés peuvent être utilisés pour identifier les points de levier élevés. L'effet de levier est une mesure de l'influence d'un point sur le modèle ajusté. Dans l’ensemble, l’utilisation de résidus studentisés permet d’analyser et d’améliorer les performances des modèles de régression.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Article chaud

Outils chauds Tags

Article chaud

Tags d'article chaud

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Techniques d'analyse résiduelle en Python
Jun 10, 2023 am 08:52 AM
Techniques d'analyse résiduelle en Python
Jun 10, 2023 am 08:52 AM
Techniques d'analyse résiduelle en Python
 AssertionError : Comment résoudre les erreurs d'assertion Python ?
Jun 25, 2023 pm 11:07 PM
AssertionError : Comment résoudre les erreurs d'assertion Python ?
Jun 25, 2023 pm 11:07 PM
AssertionError : Comment résoudre les erreurs d'assertion Python ?
 Comment développer un scanner de vulnérabilités en Python
Jul 01, 2023 am 08:10 AM
Comment développer un scanner de vulnérabilités en Python
Jul 01, 2023 am 08:10 AM
Comment développer un scanner de vulnérabilités en Python
 Techniques d'échantillonnage stratifié en Python
Jun 10, 2023 pm 10:40 PM
Techniques d'échantillonnage stratifié en Python
Jun 10, 2023 pm 10:40 PM
Techniques d'échantillonnage stratifié en Python
 Comment utiliser Python pour les scripts et l'exécution sous Linux
Oct 05, 2023 am 11:45 AM
Comment utiliser Python pour les scripts et l'exécution sous Linux
Oct 05, 2023 am 11:45 AM
Comment utiliser Python pour les scripts et l'exécution sous Linux
 Utilisation de la fonction sqrt() en Python
Feb 21, 2024 pm 03:09 PM
Utilisation de la fonction sqrt() en Python
Feb 21, 2024 pm 03:09 PM
Utilisation de la fonction sqrt() en Python
 Comment utiliser la technique de clustering vectoriel de support en Python ?
Jun 06, 2023 am 08:00 AM
Comment utiliser la technique de clustering vectoriel de support en Python ?
Jun 06, 2023 am 08:00 AM
Comment utiliser la technique de clustering vectoriel de support en Python ?
 Apprenez à utiliser la programmation Python pour réaliser l'amarrage de l'interface de reconnaissance d'image Baidu et réaliser la fonction de reconnaissance d'image.
Aug 25, 2023 pm 03:10 PM
Apprenez à utiliser la programmation Python pour réaliser l'amarrage de l'interface de reconnaissance d'image Baidu et réaliser la fonction de reconnaissance d'image.
Aug 25, 2023 pm 03:10 PM
Apprenez à utiliser la programmation Python pour réaliser l'amarrage de l'interface de reconnaissance d'image Baidu et réaliser la fonction de reconnaissance d'image.







