 Problème commun
Problème commun
 Explication détaillée de l'algorithme de tri, facile à maîtriser les compétences avancées
Explication détaillée de l'algorithme de tri, facile à maîtriser les compétences avancées
Explication détaillée de l'algorithme de tri, facile à maîtriser les compétences avancées
Les algorithmes de tri sont des outils de base en informatique et en traitement de données utilisés pour organiser les éléments dans un ordre spécifique. Qu'il s'agisse d'une liste de nombres, de chaînes ou de tout autre type de données, les algorithmes de tri jouent un rôle essentiel dans l'organisation et la manipulation efficaces des données.
Dans cet article, nous explorerons le concept des algorithmes de tri, leur importance et certains algorithmes couramment utilisés.
Qu'est-ce qu'un algorithme de tri ?
Un algorithme de tri est un processus étape par étape utilisé pour organiser les éléments dans un ordre spécifique, tel que l'ordre croissant ou décroissant. L'ordre peut être basé sur divers critères, notamment numériques, alphabétiques ou une fonction de comparaison personnalisée. Les algorithmes de tri prennent une collection non ordonnée d'éléments et les réorganisent dans l'ordre souhaité, rendant ainsi la manipulation des données et la recherche plus efficaces.
Importance des algorithmes de tri
Les algorithmes de tri jouent un rôle essentiel dans divers domaines de l'informatique et du traitement des données. Voici quelques raisons qui soulignent l'importance des algorithmes de tri :
Organisation et recherche
Les algorithmes de tri organisent les données efficacement, facilitant ainsi la recherche d'éléments spécifiques. Lors du tri des données, vous pouvez utiliser des opérations de recherche telles que la recherche binaire, dont la complexité temporelle est O(log n), au lieu de la recherche linéaire dont la complexité temporelle est O(n). Le tri améliore les performances globales du système en récupérant plus rapidement les informations d’ensembles de données volumineux.
Analyse des données
Les algorithmes de tri sont cruciaux pour les tâches d'analyse des données. Le tri de vos données dans un ordre spécifique facilite l'identification des modèles, des tendances et des valeurs aberrantes. En organisant les données selon des critères spécifiques, les analystes peuvent obtenir des informations précieuses et prendre des décisions éclairées. Le tri est une étape fondamentale du prétraitement des données avant d’appliquer des algorithmes d’analyse statistique ou d’apprentissage automatique.
Gestion des bases de données
Les bases de données stockent généralement de grandes quantités de données qui doivent être triées pour une récupération et une manipulation efficaces. Les algorithmes de tri sont utilisés dans les systèmes de gestion de bases de données pour trier les enregistrements en fonction de valeurs clés, permettant ainsi une interrogation et une indexation plus rapides. Une technologie de tri efficace permet d'optimiser les opérations de base de données, de réduire les temps de réponse et d'améliorer les performances globales du système.
Algorithmes et structures de données
Les algorithmes de tri sont les éléments constitutifs de divers algorithmes et structures de données avancés. De nombreux algorithmes, tels que les algorithmes graphiques, s'appuient sur des données triées pour un parcours et un traitement efficaces. Les structures de données telles que les arbres de recherche équilibrés et les files d'attente prioritaires utilisent souvent des algorithmes de tri en interne pour maintenir l'ordre et effectuer les opérations efficacement.
Visualisation des données
Les algorithmes de tri sont utilisés dans les applications de visualisation de données pour organiser les points de données de manière visuellement significative. Ils aident à générer des représentations visuelles ordonnées, telles que des graphiques à barres, des histogrammes et des nuages de points, permettant aux utilisateurs de comprendre plus facilement la distribution et les relations des données.
Gestion des fichiers et des enregistrements
Les algorithmes de tri sont cruciaux pour les tâches de gestion des fichiers et des enregistrements. Lorsque vous travaillez avec des fichiers ou des bases de données volumineux, les algorithmes de tri aident à organiser les enregistrements dans un ordre spécifique, facilitant ainsi la récupération, la mise à jour et la maintenance des données. Ils facilitent la fusion efficace des fichiers triés et prennent en charge des opérations telles que la déduplication et la fusion de données.
Optimisation des ressources
L'algorithme de tri permet d'optimiser les ressources système. En organisant les données de manière triée, les valeurs en double peuvent être identifiées et éliminées, améliorant ainsi l'utilisation du stockage. De plus, les algorithmes de tri peuvent aider à identifier et supprimer les données redondantes ou inutiles, réduisant ainsi les besoins de stockage et améliorant la gestion des ressources.
Conception et analyse d'algorithmes
L'algorithme de tri est la recherche fondamentale en matière de conception et d'analyse d'algorithmes. Comprendre les différents algorithmes de tri, leurs complexités et leurs compromis peut aider à développer des algorithmes efficaces pour diverses tâches informatiques. Les algorithmes de tri illustrent des concepts clés tels que la complexité temporelle, la complexité spatiale et l'efficacité des algorithmes.
Algorithmes de tri couramment utilisés
Une variété d'algorithmes de tri ont été développés, chacun avec ses propres avantages, inconvénients et caractéristiques de performance. Voici quelques algorithmes de tri couramment utilisés :
Tri à bulles
Le tri à bulles est un algorithme de tri simple basé sur une comparaison. Il compare à plusieurs reprises les éléments adjacents et les échange s'ils sont dans le mauvais ordre. L'élément le plus grand (ou le plus petit) « bulle » jusqu'à la bonne position à chaque passage. La complexité temporelle du tri à bulles est de O(n²) dans les cas les plus défavorables et moyens, ce qui le rend inefficace pour les grands ensembles de données. Cependant, il est facile à comprendre et à mettre en œuvre.
Tri par sélection
Le tri par sélection divise l'entrée en partie triée et partie non triée. Il sélectionne à plusieurs reprises l'élément le plus petit (ou le plus grand) de la section non triée et l'échange avec l'élément au début de la section non triée. La complexité temporelle du tri par sélection est de O(n²) quelle que soit l'entrée, ce qui le rend inefficace pour les grands ensembles de données. Cependant, il nécessite un échange minimal, ce qui le rend utile lorsque le coût de l’échange d’éléments est élevé.
Tri par insertion
Le tri par insertion crée une séquence triée en insérant de manière itérative des éléments de la partie non triée dans les positions correctes dans la partie triée. Il commence par un seul élément et étend progressivement la séquence de tri jusqu'à ce que la liste entière soit triée. Le tri par insertion a une complexité temporelle de O(n²), mais il fonctionne bien sur des listes petites ou partiellement triées. Cela fonctionne également bien pour le tri en ligne, où les éléments arrivent un par un.
Tri par fusion
Le tri par fusion est un algorithme diviser pour régner. Il divise l'entrée en sous-problèmes plus petits, les trie de manière récursive, puis fusionne les sous-problèmes triés pour obtenir le résultat final trié. Dans tous les cas, la complexité temporelle du tri par fusion est O(n log n), ce qui le rend très efficace pour les grands ensembles de données. Il s'agit d'un algorithme de tri stable largement utilisé dans diverses applications.
Quicksort
Quicksort est un autre algorithme diviser pour régner qui sélectionne un pivot et divise l'entrée en deux sous-problèmes : les éléments plus petits que le pivot et les éléments plus grands que le pivot. Il trie ensuite les sous-problèmes de manière récursive. Le tri rapide a une complexité temporelle moyenne de O(n log n), mais lorsque la sélection de pivot est mauvaise, sa complexité temporelle dans le pire des cas est O(n²). Cependant, en pratique, il est généralement plus rapide que les autres algorithmes de tri basés sur des comparaisons.
Tri par tas
Le tri par tas utilise la structure de données du tas binaire pour trier les éléments. Il construit d'abord un tas maximum ou un tas min en fonction de l'entrée, puis supprime à plusieurs reprises l'élément racine, qui est respectivement l'élément max ou min. Les éléments supprimés sont placés à la fin de la section triée. Dans tous les cas, la complexité temporelle du tri par tas est O(n log n). Il s'agit d'un algorithme de tri sur place, mais instable.
Tri Radix
Le tri Radix est un algorithme de tri non comparatif qui trie les éléments en fonction de leurs nombres ou de leurs caractères. Il fonctionne en triant les éléments du nombre le moins significatif au nombre le plus significatif (et vice versa). La complexité temporelle du tri par base est O(kn), où k est le nombre de nombres ou de caractères dans l'entrée. Il est très efficace pour trier des entiers ou des chaînes à l'aide de représentations de longueur fixe.
Tri par comptage
Le tri par comptage est un algorithme de tri en temps linéaire qui fonctionne en comptant le nombre de fois où chaque élément apparaît dans l'entrée et en utilisant ces informations pour déterminer leur position de tri. Il nécessite une première connaissance de la gamme d’éléments d’entrée et convient au tri d’entiers dans une plage limitée. La complexité temporelle du tri par comptage est O(n + k), où k est la plage des éléments d'entrée.
Tri par compartiment
Le tri par compartiment est un algorithme de tri basé sur la distribution qui divise l'entrée en un nombre fixe de compartiments de taille égale. Il attribue ensuite les éléments à leurs compartiments respectifs en fonction de leur valeur et trie chaque compartiment individuellement. Enfin, les seaux triés sont connectés pour obtenir le résultat final du tri. La complexité temporelle moyenne du tri par compartiments est O(n + k), où n est le nombre d'éléments et k est le nombre de compartiments.
Tri par colline
Le tri par colline est une extension du tri par insertion, qui améliore l'efficacité en comparant et en échangeant des éléments éloignés les uns des autres. Sa fonction est de trier les éléments à chaque intervalle d'intervalle en utilisant une série d'intervalles de plus en plus petits (généralement générés à l'aide d'une séquence de Knuth). La complexité temporelle du tri Hill dépend de la séquence d'intervalles utilisée, et elle est généralement considérée comme plus rapide que le tri par insertion mais plus lente que les algorithmes de tri plus complexes.
Conclusion
Ce ne sont là que quelques exemples d'algorithmes de tri, chacun avec des propriétés et des compromis uniques. La taille de l'ensemble de données, le type de données, les exigences de stabilité, les limitations de mémoire et les considérations en matière de performances ne sont que quelques exemples de variables qui influencent le choix de l'algorithme de tri. En ayant une compréhension de base des différents algorithmes de tri, vous pouvez choisir le meilleur algorithme de tri pour les besoins spécifiques de votre développeur.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Problèmes complexes de conception expérimentale sur le marché biface de Kuaishou
Apr 15, 2023 pm 07:40 PM
Problèmes complexes de conception expérimentale sur le marché biface de Kuaishou
Apr 15, 2023 pm 07:40 PM
1. Contexte du problème 1. Introduction à l'expérience du marché biface Le marché biface, c'est-à-dire une plateforme, comprend deux participants, producteurs et consommateurs, et les deux parties se promeuvent mutuellement. Par exemple, Kuaishou a un producteur vidéo et un consommateur vidéo, et les deux identités peuvent se chevaucher dans une certaine mesure. L'expérimentation bilatérale est une méthode expérimentale qui combine des groupes du côté des producteurs et des consommateurs. Les expériences bilatérales présentent les avantages suivants : (1) L'impact de la nouvelle stratégie sur deux aspects peut être détecté simultanément, tels que les changements dans le DAU du produit et le nombre de personnes téléchargeant des œuvres. Les plateformes bilatérales ont souvent des effets de réseau transversaux. Plus il y a de lecteurs, plus les auteurs seront actifs, et plus les auteurs seront actifs, plus les lecteurs suivront. (2) Le débordement et le transfert d'effet peuvent être détectés. (3) Aidez-nous à mieux comprendre le mécanisme d'action. L'expérience AB elle-même ne peut pas nous dire la relation entre la cause et l'effet, seulement.
 Comment filtrer et trier les données dans le développement de la technologie Vue
Oct 09, 2023 pm 01:25 PM
Comment filtrer et trier les données dans le développement de la technologie Vue
Oct 09, 2023 pm 01:25 PM
Comment filtrer et trier les données dans le développement de la technologie Vue Dans le développement de la technologie Vue, le filtrage et le tri des données sont des fonctions très courantes et importantes. Grâce au filtrage et au tri des données, nous pouvons rapidement interroger et afficher les informations dont nous avons besoin, améliorant ainsi l'expérience utilisateur. Cet article expliquera comment filtrer et trier les données dans Vue et fournira des exemples de code spécifiques pour aider les lecteurs à mieux comprendre et utiliser ces fonctions. 1. Filtrage des données Le filtrage des données fait référence au filtrage des données qui répondent aux exigences en fonction de conditions spécifiques. Dans Vue, on peut passer comp
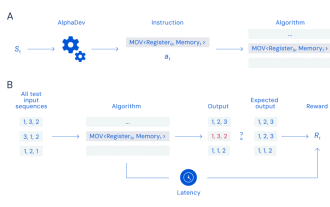 Google utilise l'IA pour briser le sceau de dix ans de l'algorithme de tri. Elle est exécutée des milliards de fois chaque jour, mais les internautes disent que c'est la recherche la plus irréaliste ?
Jun 22, 2023 pm 09:18 PM
Google utilise l'IA pour briser le sceau de dix ans de l'algorithme de tri. Elle est exécutée des milliards de fois chaque jour, mais les internautes disent que c'est la recherche la plus irréaliste ?
Jun 22, 2023 pm 09:18 PM
Tri | Nuka-Cola, Chu Xingjuan Les amis qui ont suivi des cours d'informatique de base doivent avoir personnellement conçu un algorithme de tri, c'est-à-dire utiliser du code pour réorganiser les éléments d'une liste non ordonnée par ordre croissant ou décroissant. C'est un défi intéressant, et il existe de nombreuses façons possibles de le relever. Beaucoup de temps a été investi pour trouver comment accomplir les tâches de tri plus efficacement. En tant qu'opération de base, les algorithmes de tri sont intégrés aux bibliothèques standard de la plupart des langages de programmation. Il existe de nombreuses techniques et algorithmes de tri différents utilisés dans les bases de code du monde entier pour organiser de grandes quantités de données en ligne, mais au moins en ce qui concerne les bibliothèques C++ utilisées avec le compilateur LLVM, le code de tri n'a pas changé depuis plus d'une décennie. . Récemment, l'équipe Google DeepMindAI a développé un
 Swoole Advanced : Comment utiliser le multithreading pour implémenter un algorithme de tri à grande vitesse
Jun 14, 2023 pm 09:16 PM
Swoole Advanced : Comment utiliser le multithreading pour implémenter un algorithme de tri à grande vitesse
Jun 14, 2023 pm 09:16 PM
Swoole est un framework de communication réseau hautes performances basé sur le langage PHP. Il prend en charge la mise en œuvre de plusieurs modes IO asynchrones et de plusieurs protocoles réseau avancés. Sur la base de Swoole, nous pouvons utiliser sa fonction multi-threading pour implémenter des opérations algorithmiques efficaces, telles que des algorithmes de tri à grande vitesse. L'algorithme de tri à grande vitesse (QuickSort) est un algorithme de tri courant. En localisant un élément de référence, les éléments sont divisés en deux sous-séquences. Celles plus petites que l'élément de référence sont placées à gauche et celles supérieures ou égales à la référence. L'élément est placé à droite. Ensuite, les sous-séquences gauche et droite sont placées par récursion.
 Comment implémenter l'algorithme de tri par sélection en C#
Sep 20, 2023 pm 01:33 PM
Comment implémenter l'algorithme de tri par sélection en C#
Sep 20, 2023 pm 01:33 PM
Comment implémenter l'algorithme de tri par sélection en C# Le tri par sélection (SelectionSort) est un algorithme de tri simple et intuitif. Son idée de base est de sélectionner à chaque fois l'élément le plus petit (ou le plus grand) parmi les éléments à trier et de le placer à la fin de. la séquence triée. Répétez ce processus jusqu'à ce que tous les éléments soient triés. Apprenons-en davantage sur la façon d'implémenter l'algorithme de tri par sélection en C#, ainsi que des exemples de code spécifiques. Création d'une méthode de tri par sélection Tout d'abord, nous devons créer une méthode pour implémenter le tri par sélection. Cette méthode accepte un
 Comment utiliser l'algorithme de tri par base en C++
Sep 19, 2023 pm 12:15 PM
Comment utiliser l'algorithme de tri par base en C++
Sep 19, 2023 pm 12:15 PM
Comment utiliser l'algorithme de tri par base en C++ L'algorithme de tri par base est un algorithme de tri non comparatif qui termine le tri en divisant les éléments à trier en un ensemble limité de chiffres. En C++, nous pouvons utiliser l’algorithme de tri par base pour trier un ensemble d’entiers. Ci-dessous, nous verrons en détail comment implémenter l'algorithme de tri par base, avec des exemples de code spécifiques. Idée d'algorithme L'idée de l'algorithme de tri par base est de diviser les éléments à trier en un ensemble limité de bits numériques, puis de trier les éléments sur chaque bit tour à tour. Le tri sur chaque bit est terminé
 Quels sont les algorithmes de tri des tableaux ?
Jun 02, 2024 pm 10:33 PM
Quels sont les algorithmes de tri des tableaux ?
Jun 02, 2024 pm 10:33 PM
Les algorithmes de tri de tableaux sont utilisés pour organiser les éléments dans un ordre spécifique. Les types courants d'algorithmes incluent : Tri à bulles : échangez les positions en comparant les éléments adjacents. Tri par sélection : recherchez le plus petit élément et remplacez-le par la position actuelle. Tri par insertion : insérez les éléments un par un à la bonne position. Tri rapide : méthode diviser pour mieux régner, sélectionnez l'élément pivot pour diviser le tableau. Tri par fusion : diviser pour mieux régner, tri récursif et fusion de sous-tableaux.
 Discussion sur les scénarios d'application de différents algorithmes de tri de tableaux PHP
Apr 28, 2024 am 09:39 AM
Discussion sur les scénarios d'application de différents algorithmes de tri de tableaux PHP
Apr 28, 2024 am 09:39 AM
Pour différents scénarios, il est crucial de choisir l’algorithme de tri des tableaux PHP approprié. Le tri à bulles convient aux tableaux à petite échelle sans exigences de stabilité ; le tri rapide a la complexité temporelle la plus faible dans la plupart des cas ; le tri par fusion a une stabilité élevée et convient aux scénarios qui nécessitent des résultats stables ; le tri par sélection convient aux situations sans exigences de stabilité. Le tri par tas trouve efficacement la valeur maximale ou minimale. Grâce à la comparaison de cas réels, le tri rapide est supérieur aux autres algorithmes en termes d'efficacité temporelle, mais le tri par fusion doit être choisi lorsque la stabilité doit être prise en compte.




