Classification des bruits cardiaques par apprentissage profond basée sur un spectrogramme logarithmique

Cet article est très intéressant. Il propose deux modèles de classification des sons de la fréquence cardiaque basés sur le spectrogramme logarithmique du signal sonore du cœur. Nous savons tous que les spectrogrammes sont largement utilisés en reconnaissance vocale. Cet article traite le signal sonore cardiaque comme un signal vocal et obtient de bons résultats

Le signal sonore cardiaque est divisé en images de longueur constante et ses caractéristiques de spectrogramme logarithmique sont extraites. L'article propose une mémoire à long terme (LSTM) et. Deux modèles d'apprentissage profond, le réseau neuronal convolutif (CNN), classent les sons des battements cardiaques en fonction des caractéristiques extraites.

Ensemble de données sur les sons cardiaques

Le diagnostic d'imagerie comprend l'imagerie par résonance magnétique cardiaque (IRM), la tomodensitométrie et l'imagerie de perfusion myocardique. Les inconvénients de ces technologies sont également évidents : des exigences élevées envers les machines et les professionnels modernes et des temps de diagnostic longs.

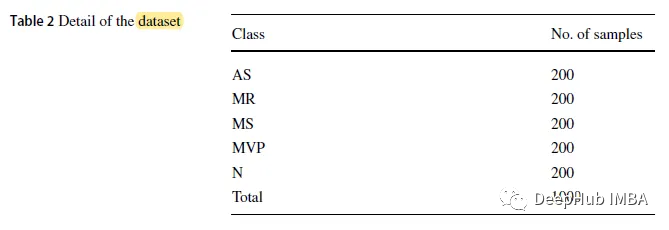
L'ensemble de données utilisé dans cet article est un ensemble de données publiques, qui contient 1 000 échantillons de signaux au format .wav avec une fréquence d'échantillonnage de 8 kHz. L'ensemble de données est divisé en 5 catégories, dont 1 catégorie normale (N) et 4 catégories anormales : sténose aortique (SA), régurgitation mitrale (MR), sténose mitrale (MS) et régurgitation valvulaire mitrale (MR). )

La sténose aortique (SA) se produit lorsque la valvule aortique est trop petite, étroite ou rigide. Le souffle typique de la sténose aortique est un souffle aigu en forme de losange.

La régurgitation mitrale (MR) se produit lorsque la valvule mitrale du cœur ne se ferme pas correctement, provoquant le retour du sang dans le cœur au lieu d'être pompé. Lors de l'auscultation du cœur fœtal, le son de S1 peut être faible (parfois fort) jusqu'à ce que le volume du murmure augmente de S2. En raison du débit mitral rapide après S3, un souffle mi-diastolique court et grondant peut être entendu

La sténose mitrale (SEP) signifie que la valvule mitrale est endommagée et ne peut pas s'ouvrir complètement. L'auscultation des bruits cardiaques montre que S1 s'aggrave en cas de sténose mitrale précoce et devient mou en cas de sténose mitrale sévère. À mesure que l’hypertension pulmonaire se développe, le son S2 sera accentué. Les patients atteints de SEP pure n'ont pratiquement pas de S3 ventriculaire gauche.

Le prolapsus de la valve mitrale (MVP) fait référence au prolapsus des feuillets de la valve mitrale dans l'oreillette gauche pendant la contraction cardiaque. La MVP est généralement bénigne mais peut entraîner des complications telles qu'une régurgitation mitrale, une endocardite et une rupture du cordon. Les signes incluent des clics mi-systoliques et des souffles systoliques tardifs (en cas de régurgitation)

Prétraitement et extraction de caractéristiques

Les signaux sonores ont des longueurs différentes, les échantillons doivent donc être corrigés pour chaque fichier enregistré. Pour garantir que le signal sonore contient au moins un cycle cardiaque complet, nous réduisons la longueur. Étant donné qu'un cœur adulte bat 65 à 75 fois par minute et que le cycle de battement cardiaque dure environ 0,8 seconde, nous avons coupé les échantillons de signal en segments de 2,0 secondes, 1,5 seconde et 1,0 seconde

Sur la base de la transformée de Fourier discrète ( DFT), les bruits cardiaques sont La forme d'onde originale du signal est convertie en un spectrogramme logarithmique. La DFT y(k) du signal sonore est l'équation (1) et le spectre logarithmique s est défini par l'équation (2).

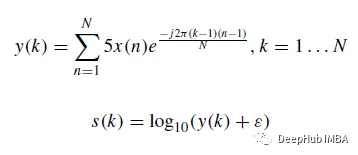
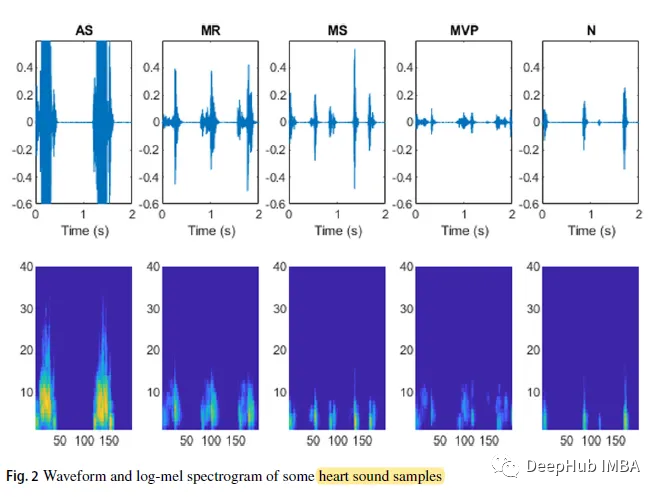
Dans la formule, N est la longueur du vecteur x et ε = 10^(- 6) est un petit décalage. Les formes d'onde et les spectrogrammes logarithmiques de certains échantillons de bruits cardiaques sont les suivants :

Modèle d'apprentissage profond

1, LSTM

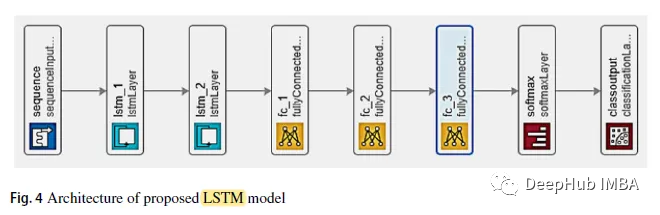
Le modèle LSTM est conçu avec 2 couches de connexion directe, puis 3 couches de connexion complète. La troisième couche entièrement connectée entre dans le classificateur softmax.

2. Modèle CNN

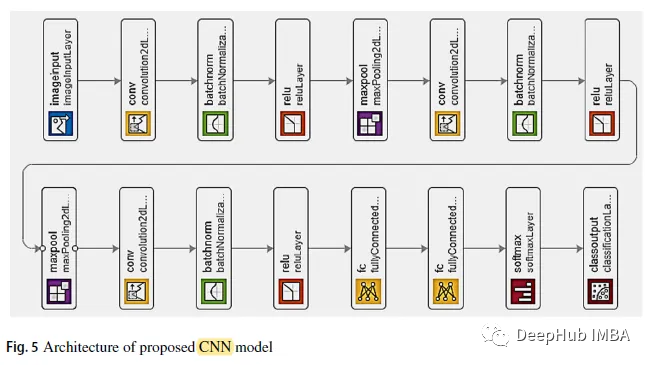
Comme le montre la figure ci-dessus, les deux premières couches convolutives sont suivies d'une couche de pooling maximale qui se chevauche. La troisième couche convolutive est directement connectée à la première couche entièrement connectée. La deuxième couche entièrement connectée est transmise à un classificateur softmax avec cinq étiquettes de classe. Utilisation de BN et ReLU après chaque couche convolutionnelle

3. Détails de la formation

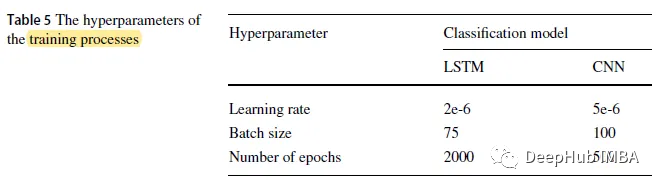
Résultats

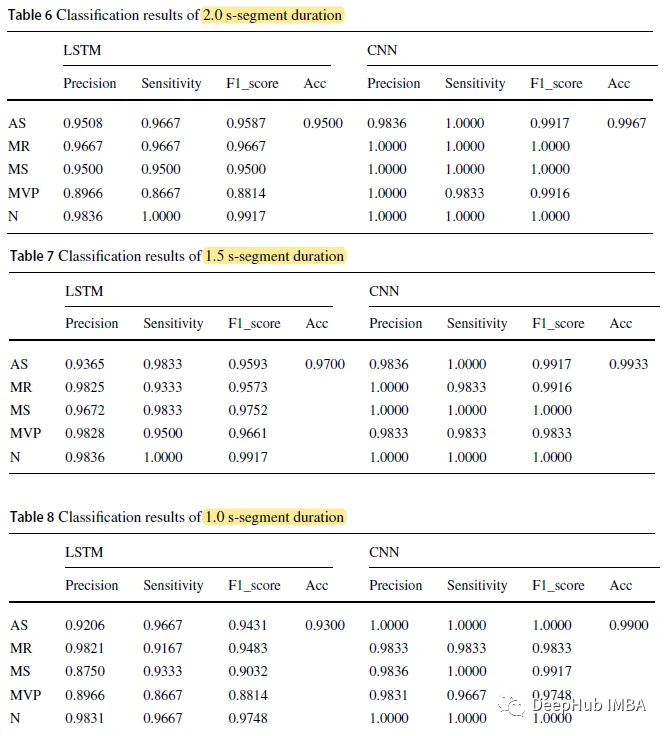
L'ensemble de formation occupe 70 % de l'ensemble des données, tandis que l'ensemble de test contient le reste. partie

Lorsque la durée du segment du modèle CNN est de 2,0 s, la précision la plus élevée est de 0,9967 ; la précision LSTM avec un temps de segmentation de 1,0 s est la plus basse de 0,9300.

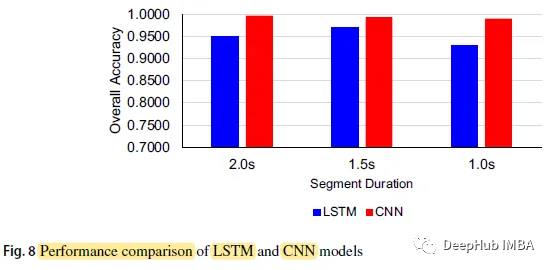
La précision globale du modèle CNN est respectivement de 0,9967, 0,9933 et 0,9900, et la durée du segment est respectivement de 2,0 secondes, 1,5 seconde et 1,0 seconde, tandis que les trois chiffres du modèle LSTM sont respectivement de 0,9500, 0,9700 et 0,9300

CNN La précision de prédiction du modèle sur différentes périodes de temps est supérieure à celle du modèle LSTM

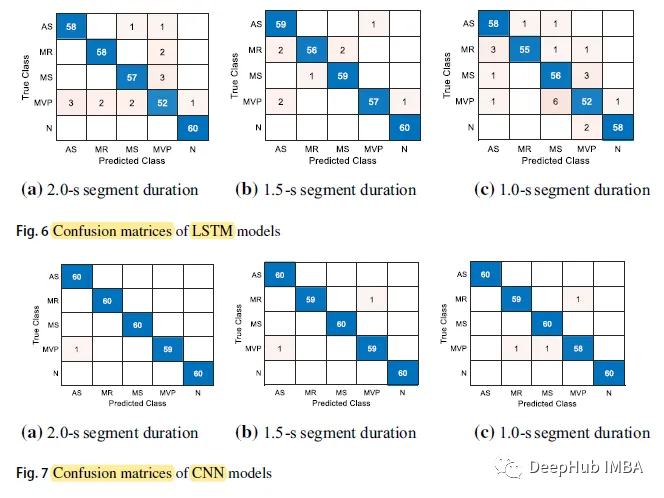
Voici la matrice de confusion :

La classe N (Normal) a la précision de prédiction la plus élevée, atteignant 60 dans 5 cas, tandis que la classe MVP a la précision de prédiction la plus faible parmi tous les cas.

La durée d'entrée du modèle LSTM est de 2,0 s et le temps de prédiction le plus long est de 9,8631 ms. Le modèle CNN avec un temps de classification de 1,0 s a le temps de prédiction le plus court, soit 4,2686 ms.

Par rapport à d'autres SOTA, certaines études ont une très grande précision, mais ces études n'impliquent que deux catégories (normales et anormales), alors que notre étude est divisée en cinq catégories

Par rapport à d'autres études utilisant le même ensemble de données (0,9700), l'étude papier s'est considérablement améliorée, avec la plus grande précision de 0,9967.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!