Décomposition de distributions multimodales à l'aide de modèles de mélange gaussiens

La distribution multimodale unidimensionnelle peut être divisée en plusieurs distributions à l'aide du modèle de mélange gaussien

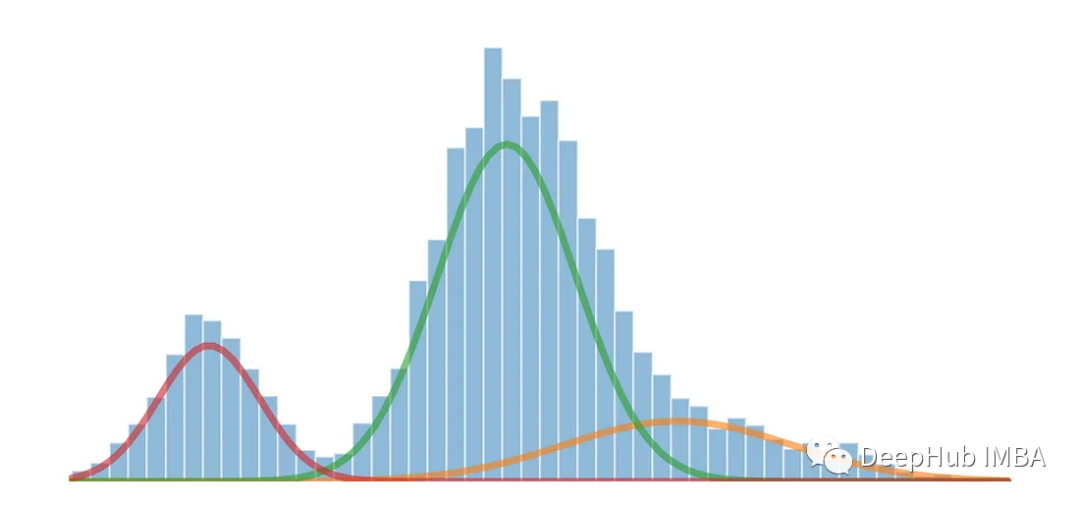
Les modèles de mélange gaussien (GMM) sont une méthode couramment utilisée dans les domaines des statistiques et de l'apprentissage automatique. Modèles probabilistes pour la modélisation et analyser des distributions de données complexes. GMM est un modèle génératif qui suppose que les données observées sont composées de plusieurs distributions gaussiennes, chaque distribution gaussienne est appelée une composante et ces composantes contrôlent leur contribution dans les données via des pondérations.

Générer des données avec des distributions multimodales

Lorsqu'un ensemble de données affiche plusieurs pics ou modes différents, cela signifie généralement qu'il existe plusieurs clusters ou concentrations de points de données importants dans l'ensemble de données. Chaque mode représente un cluster ou une concentration important de points de données dans la distribution et peut être considéré comme une région à haute densité où les valeurs de données sont plus susceptibles de se produire

Nous utiliserons un tableau unidimensionnel généré par numpy .

import numpy as np  dist_1 = np.random.normal(10, 3, 1000) dist_2 = np.random.normal(30, 5, 4000) dist_3 = np.random.normal(45, 6, 500)  multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)

Visualisons la distribution unidimensionnelle des données.

import matplotlib.pyplot as plt import seaborn as sns sns.set_style('whitegrid')  plt.hist(multimodal_dist, bins=50, alpha=0.5) plt.show()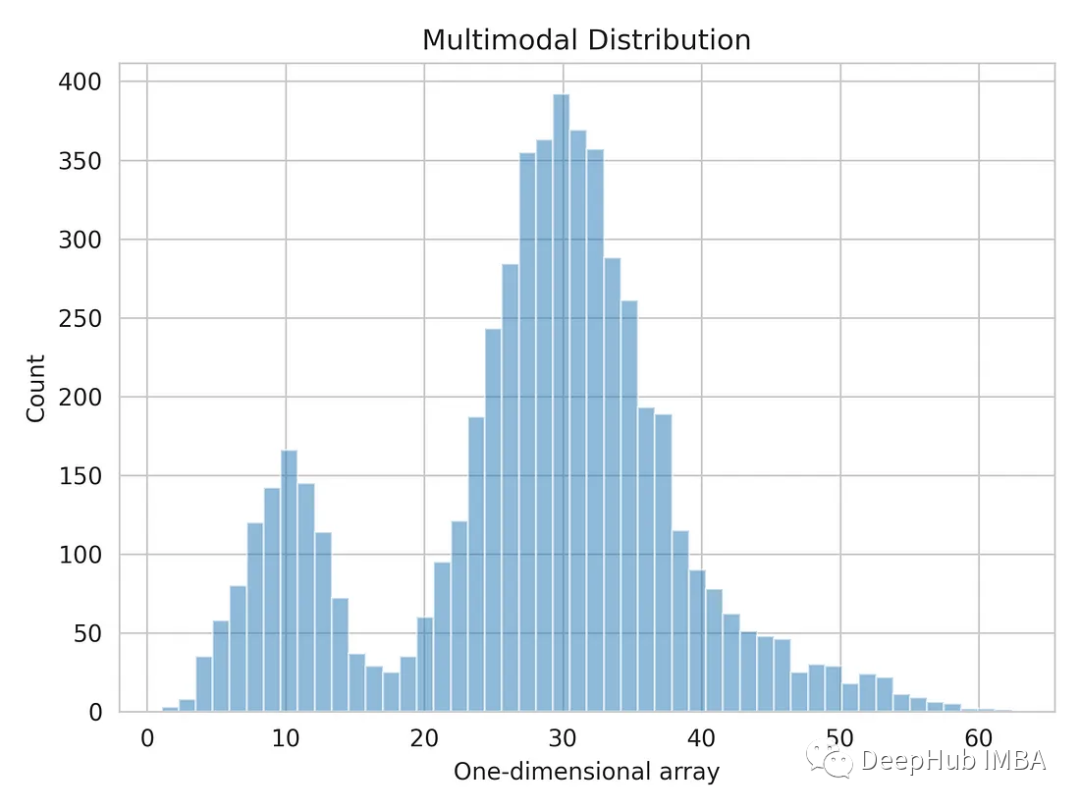

Distribution multimodale divisée à l'aide du modèle de mélange gaussien

Nous utiliserons le modèle de mélange gaussien pour calculer la moyenne et l'écart type de chaque distribution afin de séparer la distribution multimodale en trois distributions originales. Le modèle de mélange gaussien est un modèle probabiliste non supervisé qui peut être utilisé pour le regroupement de données. Il utilise l'algorithme de maximisation des attentes pour estimer la région de densité

from sklearn.mixture import GaussianMixture  gmm = GaussianMixture(n_compnotallow=3) gmm.fit(multimodal_dist.reshape(-1, 1))  means = gmm.means_  # Conver covariance into Standard Deviation standard_deviations = gmm.covariances_**0.5  # Useful when plotting the distributions later weights = gmm.weights_   print(f"Means: {means}, Standard Deviations: {standard_deviations}")  #Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]

Nous avons déjà la moyenne et l'écart type pour modéliser la distribution d'origine. Vous pouvez constater que même si la moyenne et l’écart type ne sont pas tout à fait corrects, ils fournissent une estimation proche.

Comparez nos estimations avec les données originales.

from scipy.stats import norm  fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))  for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):axes[0].hist(dist, bins=bins, alpha=0.5)  axes[1].hist(multimodal_dist, bins=50, alpha=0.5)  x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)  for mean, covariance, weight in zip(means, standard_deviations, weights):pdf = weight*norm.pdf(x, mean, std)plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)  plt.show()

Résumé

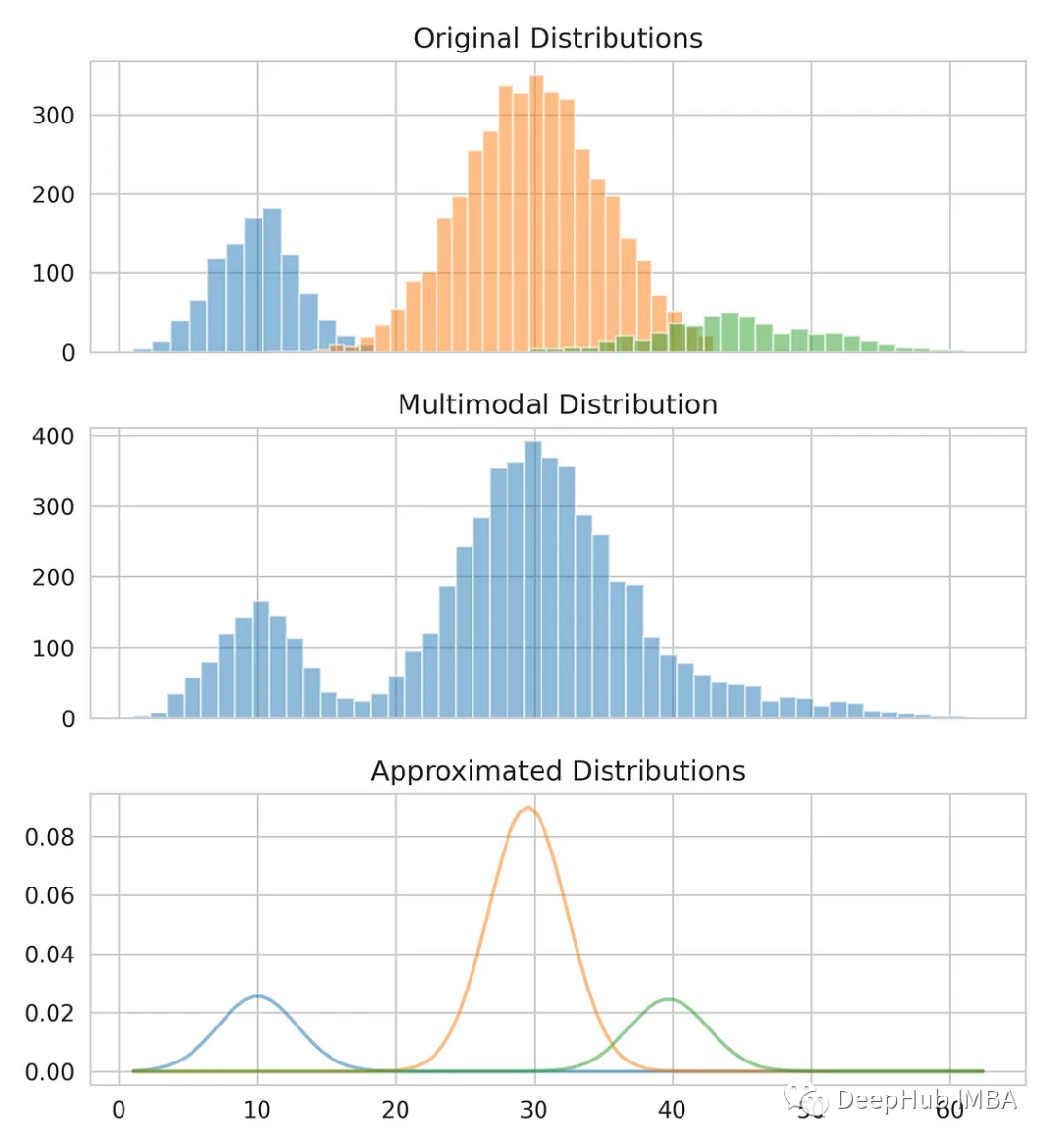
Le modèle de mélange gaussien est un outil puissant qui peut être utilisé pour modéliser et analyser des distributions de données complexes, et est également l'un des fondements de nombreux algorithmes d'apprentissage automatique. Elle a un large éventail d'applications et peut résoudre divers problèmes de modélisation et d'analyse de données

Cette méthode peut être utilisée comme technique d'ingénierie de fonctionnalités pour estimer l'intervalle de confiance d'une sous-distribution dans la variable d'entrée

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!