Quelle est la longueur minimale de ruban de papier nécessaire pour réaliser une bande de Möbius ? Un mystère vieux de 50 ans résolu

Avez-vous déjà réalisé vous-même une bande de Mobius ?

La bande de Möbius est une structure mathématique particulière. Il est en fait très simple de construire une si belle surface à un seul côté, même un enfant peut facilement la réaliser. Il vous suffit de prendre un morceau de ruban adhésif, de le tordre une fois et de coller les deux extrémités ensemble. Cependant, une bande de Möbius aussi facile à réaliser possède des propriétés complexes qui suscitent depuis longtemps l’intérêt des mathématiciens.

Récemment, les chercheurs ont été troublés par une question apparemment simple : quelle est la longueur minimale de ruban de papier requise pour fabriquer une bande de Möbius ? Richard Evan Schwartz de l'Université Brown a déclaré que ce problème n'est pas résolu pour les bandes de Möbius car elles sont « intégrées » plutôt qu'« immergées », ce qui signifie qu'elles ne se pénètrent pas ou ne se croisent pas. Une bande de Möbius est en fait un hologramme, une figure projetée dans un espace tridimensionnel : pour une bande de Möbius « immergée », plusieurs couches de bandes peuvent se chevaucher, un peu comme un fantôme traversant un mur pour un Möbius « encastré » ; strip, il n'y a pas de tel chevauchement.

En 1977, les mathématiciens Charles Sidney Weaver et Benjamin Rigler Halpern ont posé ce problème des dimensions minimales, notant qu'il était simple si les bandes de Möbius pouvaient se croiser. Le problème restant est donc de déterminer l’espace nécessaire pour éviter l’auto-intersection. Halpern et Weaver ont proposé une taille minimale, mais ils ont été incapables de prouver cette idée, c'est pourquoi elle est devenue connue sous le nom de conjecture de Halpern-Weaver.

Schwartz a découvert ce problème pour la première fois il y a quatre ans et en a été fasciné une fois qu'il en a pris connaissance. Aujourd’hui, son intérêt s’est transformé en de nouveaux fruits.

Adresse de l'article : https://arxiv.org/pdf/2308.12641.pdf

Il a prouvé Halpern dans un article préimprimé publié sur arXiv.org le 24 août 2023 -Conjecture de Weaver. Il a démontré que les bandes de Möbius « intégrées » en papier ne peuvent être construites qu'avec des rapports d'aspect supérieurs à . Par exemple, si la longueur du bracelet est de 1 cm, sa largeur doit être supérieure à cm.

Résoudre ce puzzle nécessite une créativité mathématique. Lorsque l’on adopte des approches standard pour résoudre ce type de problème, il est difficile de faire la distinction entre les surfaces auto-entrecroisées et non auto-entrecroisées à l’aide de formules. Il faut la vision géométrique de Schwartz pour surmonter cette difficulté, mais cela est rare.

Dans la preuve de Schwartz, il a réussi à décomposer le problème en parties traitables, dont chacune ne nécessite fondamentalement que des connaissances de base en géométrie pour être résolue.

En fait, Schwartz a essayé d'autres stratégies par intermittence pendant plusieurs années avant d'en trouver une qui fonctionnait. Il a récemment décidé de revenir sur le problème car il avait toujours estimé que la méthode qu’il avait utilisée dans un article de 2021 devait être valable.

Évidemment, son intuition était correcte. Lorsqu'il a revisité le problème, il a remarqué une erreur dans le lemme impliquant les diagrammes en T dans l'article précédent. En corrigeant cette erreur, Schwartz a rapidement et facilement prouvé la conjecture de Halpern-Weaver. Schwartz lui-même dit que sans cette erreur, il aurait résolu le problème il y a trois ans.

                                                                                                                                                                                                                                   ^{​​​​​​. Ce lemme est basé sur une idée de base : certaines lignes droites sur une bande de Möbius sont appelées surfaces réglées. Schwartz a souligné qu'une bande de papier dans l'espace, même si elle se trouve dans une position compliquée, est toujours traversée par une ligne droite en chaque point. Vous pouvez imaginer dessiner ces lignes droites de manière à ce qu'elles traversent la bande de Möbius et que les deux extrémités se touchent. la frontière.}

Dans des travaux antérieurs, Schwartz a identifié deux lignes droites parallèles entre elles et dans le même plan, qui formaient un motif en forme de T dans chaque bande de Möbius. Il souligne qu’il n’est pas évident que ces choses existent et qu’elles doivent être prouvées, ce qui constitue la première partie de la preuve du lemme.

L'étape suivante consiste à configurer et à résoudre le problème d'optimisation, qui nécessite de couper une bande de Möbius en biais le long d'un segment de ligne s'étendant sur la largeur de la bande et d'obtenir la forme finale. Schwartz a conclu à tort dans son article de 2021 que la forme était un parallélogramme.

Cet été, Schwartz a décidé d'essayer une stratégie différente. Il a commencé à essayer d'aplatir la bande de Möbius. S’il pouvait être démontré qu’ils peuvent être pressés sur une surface plane, ce problème complexe serait réduit à un problème de surface plane plus traitable. Dans une expérience, Schwartz a ouvert une bande de Möbius et s'est rendu compte qu'il ne s'agissait pas d'un parallélogramme mais d'un trapèze.

Enfin, la question vieille de 50 ans a trouvé une réponse. Il faut du courage pour tenter de résoudre un problème de longue date, et c'est là la force de Schwartz en mathématiques : il aime travailler sur des problèmes qui semblent relativement faciles mais qui sont en réalité difficiles. Il verra des problèmes que les chercheurs précédents n’avaient pas remarqués.

^{Lien de référence : https://www.scientificamerican.com/article/mathematicians-solve-50-year-old-moebius-strip-puzzle1/}

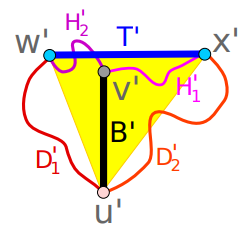
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!