Révéler les secrets de la « géométrie atomique » : l'apprentissage automatique est le moteur du développement des mathématiques

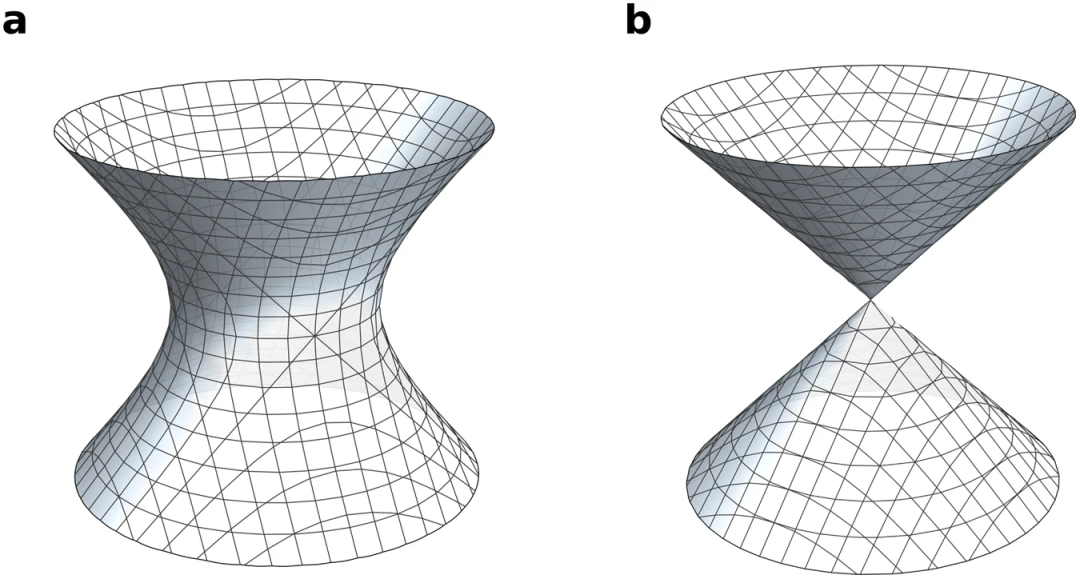
Une variété algébrique est un ensemble défini par plusieurs équations polynomiales. C'est un concept important en géométrie algébrique et étudie les propriétés de l'ensemble des solutions aux équations polynomiales dans l'espace géométrique. Les équations des variétés algébriques peuvent être de n'importe quelle dimension et peuvent être des équations dans le domaine des nombres réels ou des équations dans le domaine des nombres complexes. L'étude des propriétés des variétés algébriques peut nous aider à comprendre la distribution et la forme géométrique des racines des équations polynomiales

La géométrie algébrique est une discipline qui intègre les deux branches des mathématiques, l'algèbre et la géométrie. D'une part, cela implique l'algèbre, c'est-à-dire l'étude des propriétés et des solutions des équations, d'autre part, cela implique également la géométrie, c'est-à-dire l'étude des propriétés et des caractéristiques des formes ; Le but de la géométrie algébrique est d'appliquer des méthodes algébriques abstraites à la géométrie pour résoudre des problèmes liés aux formes, surfaces, espaces et courbes complexes et concrètes.

Le problème fondamental de la géométrie algébrique est de classer l'ensemble de solutions d'un ensemble d'équations polynomiales. , en termes simples, consiste à classer l’espace. L'objet fondamental de ses recherches est appelé variété algébrique, qui est la représentation géométrique de l'ensemble solution d'équations polynomiales.

La variété Fano (variété Fano) est un type important de variété algébrique. Dans un sens, ce sont des « morceaux atomiques » de formes mathématiques. Les variétés Fano jouent également un rôle important dans la théorie des cordes.

Contenu réécrit : Les clusters Fano sont les éléments de base des formes géométriques. Ce sont des "blocs atomiques" de formes mathématiques. Les dernières recherches sur la classification des amas de Fano incluent l'analyse d'un type d'invariance appelé périodicité quantique. Une période quantique est une séquence d'entiers utilisée pour fournir une empreinte numérique pour un cluster Fano. On suppose que les propriétés géométriques de l'amas de Fano peuvent être récupérées directement à partir de sa période quantique, si cette hypothèse se vérifie

Récemment, des mathématiciens de l'Université de Nottingham et de l'Imperial College de Londres ont utilisé pour la première fois l'apprentissage automatique pour étendre et accélérer l'analyse de « L'étude des formes atomiques. Ces "formes atomiques" sont les éléments constitutifs des formes géométriques de base des dimensions supérieures

Plus précisément, les chercheurs ont appliqué l'apprentissage automatique à une question : la période quantique de X connaît-elle les dimensions de X ? Notez qu’il n’y a aucune compréhension théorique de cela. La recherche montre qu’un simple réseau neuronal à action directe peut déterminer les dimensions de X avec une précision de 98 %. Sur cette base, les chercheurs ont établi des propriétés asymptotiques strictes au sein de la période quantique d’une classe d’amas de Fano. Ces propriétés asymptotiques déterminent les dimensions de la période quantique de X. Les résultats montrent que l’apprentissage automatique peut identifier des structures à partir de données mathématiques complexes en l’absence de compréhension théorique. Ils fournissent également des preuves positives de la conjecture selon laquelle la période quantique de l'amas de Fano détermine la diversité.

La recherche s'intitule « Dimensions of Fanno Diversity in Machine Learning » et a été publiée dans « Nature Communications » le 8 septembre 2023

Lien papier : https://www.nature .com/ articles/s41467-023-41157-1

Il y a plusieurs années, l'équipe de recherche a commencé à travailler sur la création d'un tableau périodique des formes. Ils ont appelé les fragments atomiques des amas de Fano. L'équipe a associé une séquence de nombres appelés cycles quantiques à chaque forme pour fournir un « code-barres » ou une « empreinte digitale » qui décrit la forme. Récemment, ils ont réussi à passer au crible rapidement ces codes-barres en utilisant une nouvelle méthode d'apprentissage automatique, leur permettant d'identifier des formes et leurs propriétés, comme les dimensions de chaque forme

Alexander Kasprzyk a déclaré : "Pour les mathématiciens, la clé L'étape est d'identifier le modèle dans un problème donné. Cela peut être très difficile et certaines théories mathématiques peuvent prendre des années à découvrir, a déclaré le professeur Tom Coates : "C'est là que l'intelligence artificielle peut vraiment révolutionner les mathématiques. , parce que nous avons montré que l'apprentissage automatique est efficace. un outil puissant pour découvrir des modèles dans des domaines complexes tels que l'algèbre et la géométrie. »

Sara Veneziale a déclaré : « Nous sommes très enthousiasmés par le fait que l'apprentissage automatique puisse être utilisé dans les mathématiques pures. ."

Dans l'ensemble, cette recherche montre que l'apprentissage automatique est capable de découvrir des structures jusqu'alors inconnues dans des données mathématiques complexes et constitue un outil puissant pour développer des résultats mathématiques rigoureux. Cela fournit également la preuve de la conjecture de base du programme de variété Fano : la période quantique régulière de la variété Fano détermine ce changement

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!