​Avec près de la moitié des paramètres, les performances sont proches de Google Minerva, un autre grand modèle mathématique est open source

De nos jours, les modèles de langage formés sur diverses données textuelles mixtes montreront des capacités de compréhension et de génération du langage très générales et peuvent être utilisés comme modèles de base pour s'adapter à diverses applications. Les applications telles que le dialogue ouvert ou le suivi d'instructions nécessitent des performances équilibrées sur l'ensemble de la distribution naturelle du texte et préfèrent donc les modèles à usage général.

Mais si vous souhaitez maximiser les performances dans un certain domaine (comme la médecine, la finance ou la science), alors un modèle de langage spécifique à un domaine peut fournir des capacités supérieures à un coût de calcul donné, ou à un coût plus faible. le coût de calcul fournit un niveau de capacité donné.

Des chercheurs de l'Université de Princeton, d'EleutherAI et d'autres ont formé un modèle de langage spécifique à un domaine pour résoudre des problèmes mathématiques. Ils pensent que : premièrement, la résolution de problèmes mathématiques nécessite une correspondance de modèles avec une grande quantité de connaissances professionnelles préalables, c'est donc un environnement idéal pour la formation à l'adaptation au domaine ; un raisonnement mathématique fort Les modèles linguistiques sont en amont de nombreux sujets de recherche, tels que la modélisation des récompenses, l'apprentissage par renforcement par inférence et le raisonnement algorithmique.

Ils proposent donc une méthode pour adapter les modèles de langage aux mathématiques grâce à un pré-entraînement continu de Proof-Pile-2. Proof-Pile-2 est un mélange de texte et de code liés aux mathématiques. L'application de cette approche à Code Llama aboutit à LLEMMA : un modèle de langage de base pour 7B et 34B, avec des capacités mathématiques considérablement améliorées.

Adresse papier : https://arxiv.org/pdf/2310.10631.pdf

Adresse du projet : https://github.com/EleutherAI/math-lm

LLEMMA Les performances mathématiques à 4 coups du 7B dépassent de loin celles du Google Minerva 8B, et les performances du LLEMMA 34B sont proches de celles du Minerva 62B avec près de la moitié des paramètres.

Plus précisément, les contributions de cet article sont les suivantes :

• 1 Formation et publication du modèle LLEMMA : modèles de langage 7B et 34B spécifiquement pour les mathématiques. Le modèle LLEMMA constitue l'état de l'art en matière de modèles de base rendus publics sur MATH.
• 2. Sortie d'AlgebraicStack, un ensemble de données contenant 11 octets de jetons de code spécifiquement liés aux mathématiques.
• 3. Démontré que LLEMMA est capable de résoudre des problèmes mathématiques à l'aide d'outils informatiques, à savoir un interpréteur Python et un prouveur formel de théorèmes.
• 4. Contrairement aux modèles de langage mathématique précédents (tels que Minerva), le modèle LLEMMA est ouvert. Les chercheurs ont mis les données et le code de formation à la disposition du public. Cela fait de LLEMMA une plateforme pour de futures recherches en raisonnement mathématique.

Présentation de la méthode

LLEMMA est un modèle de langage 70B et 34B spécifiquement utilisé en mathématiques. Il s'obtient en continuant à pré-entraîner le code Llama sur Proof-Pile-2.

DONNÉES : Proof-Pile-2

Les chercheurs ont créé Proof-Pile-2, qui est un article scientifique symbolique de 55 B, des données de réseau contenant des mathématiques et un mélange de codes mathématiques. La date limite de connaissance pour Proof-Pile-2 est avril 2023, à l'exception du sous-ensemble des étapes de preuve Lean.

Les outils informatiques tels que les simulations numériques, les systèmes de calcul formel et les prouveurs de théorèmes formels sont de plus en plus importants pour les mathématiciens. Par conséquent, les chercheurs ont créé AlgebraicStack, un ensemble de données de jetons de 11 B contenant du code source en 17 langues, couvrant les mathématiques numériques, les mathématiques symboliques et les mathématiques formelles. L'ensemble de données se compose de codes filtrés de Stack, de référentiels publics GitHub et de données d'étape de preuve formelle. Le tableau 9 montre le nombre de jetons pour chaque langue dans AlgebraicStack.

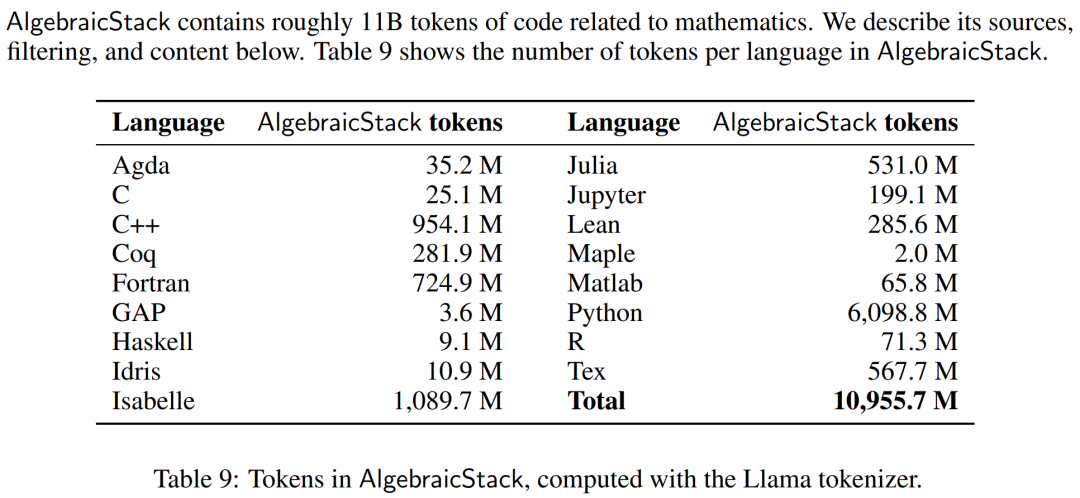
Le nombre de jetons dans chaque langue dans AlgebraicStack.

Les chercheurs ont utilisé OpenWebMath, un ensemble de données de 15 milliards de jetons composé de pages Web de haute qualité, filtrées pour le contenu mathématique. OpenWebMath filtre les pages Web CommonCrawl en fonction de mots-clés liés aux mathématiques et de scores mathématiques basés sur un classificateur, préserve le formatage mathématique (par exemple, LATEX, AsciiMath) et inclut des filtres de qualité supplémentaires (par exemple, plexité, domaine, longueur) et une quasi-duplication.

De plus, les chercheurs ont également utilisé le sous-ensemble ArXiv de RedPajama, qui est une version ouverte de l'ensemble de données de formation LLaMA. Le sous-ensemble ArXiv contient 29 milliards de morceaux. Le mélange de formation se compose d’une petite quantité de données générales du domaine et agit comme un régularisateur. Étant donné que l’ensemble de données de pré-formation pour LLaMA 2 n’est pas encore accessible au public, les chercheurs ont utilisé Pile comme ensemble de données de formation alternatif.

Modèle et formation

Chaque modèle est initialisé à partir de Code Llama, qui est à son tour initialisé à partir de Llama 2, en utilisant une structure de transformateur de décodeur uniquement, avec un jeton de code 500B fabriqué à partir de la formation. Les chercheurs ont continué à entraîner le modèle Code Llama sur Proof-Pile-2 en utilisant l'objectif standard de modélisation de langage autorégressif. Ici, le modèle LLEMMA 7B dispose de 200 milliards de jetons et le modèle LLEMMA 34B dispose de 50 milliards de jetons.

Les chercheurs ont utilisé la bibliothèque GPT-NeoX pour entraîner les deux modèles ci-dessus avec une précision mixte bfloat16 sur 256 GPU A100 de 40 Go. Ils ont utilisé le parallélisme tensoriel avec une taille mondiale 2 pour LLEMMA-7B et le parallélisme tensoriel avec une taille mondiale 8 pour 34B, ainsi que les états d'optimisation de fragments ZeRO Stage 1 sur des répliques parallèles aux données. Flash Attention 2 est également utilisé pour augmenter le débit et réduire davantage les besoins en mémoire.

LLEMMA 7B a été entraîné pour 42 000 étapes, avec une taille de lot globale de 4 millions de jetons et une longueur de contexte de 4 096 jetons. Cela équivaut à 23 000 heures A100. Le taux d'apprentissage s'élève à 1·10^−4 après 500 pas, puis décroît jusqu'à 1/30 du taux d'apprentissage maximum après 48 000 pas.

LLEMMA 34B a été entraîné pour 12 000 étapes, la taille globale du lot est également de 4 millions de jetons et la longueur du contexte est de 4 096. Cela équivaut à 47 000 heures A100. Le taux d'apprentissage s'élève à 5·10^−5 après 500 pas, puis diminue à 1/30 du taux d'apprentissage maximal.

Résultats de l'évaluation

Dans la partie expérimentale, les chercheurs visaient à évaluer si LLEMMA pouvait être utilisé comme modèle de base pour les textes mathématiques. Ils utilisent une évaluation en quelques étapes pour comparer les modèles LLEMMA et se concentrent principalement sur les modèles SOTA qui ne sont pas affinés sur des échantillons supervisés de tâches mathématiques.

Les chercheurs ont d’abord utilisé le raisonnement en chaîne de pensée et les méthodes de vote majoritaire pour évaluer la capacité de LLEMMA à résoudre des problèmes mathématiques. Les critères d’évaluation comprenaient MATH et GSM8k. Explorez ensuite l’utilisation d’outils à quelques coups et la démonstration de théorèmes. Enfin, l'impact de la mémoire et du mixage des données est étudié.

Résoudre des problèmes mathématiques à l'aide de chaînes de pensées (CoT)

Ces tâches incluent la génération de réponses textuelles indépendantes à des questions représentées en LATEX ou en langage naturel sans avoir besoin d'outils externes. Les critères d'évaluation utilisés par les chercheurs incluent MATH, GSM8k, OCWCourses, SAT et MMLU-STEM.

Les résultats sont présentés dans le tableau 1 ci-dessous. La pré-formation continue de LLEMMA sur le corpus Proof-Pile-2 a amélioré les performances de quelques échantillons sur 5 benchmarks mathématiques. Parmi eux, LLEMMA 34B s'est amélioré de 20 points sur GSM8k. que Code Llama en points de pourcentage, 13 points de pourcentage de plus que Code Llama sur MATH. Dans le même temps, le LLEMMA 7B a surpassé le modèle propriétaire Minerva.

Par conséquent, les chercheurs ont conclu qu'une pré-formation continue sur Proof-Pile-2 peut aider à améliorer la capacité du modèle pré-entraîné à résoudre des problèmes mathématiques.

Utiliser des outils pour résoudre des problèmes mathématiques

Ces tâches incluent l'utilisation d'outils de calcul pour résoudre des problèmes. Les critères d'évaluation utilisés par les chercheurs incluent MATH+Python et GSM8k+Python.

Les résultats sont présentés dans le tableau 3 ci-dessous, LLEMMA surpasse Code Llama sur les deux tâches. Les performances sur MATH et GSM8k en utilisant les deux outils sont également meilleures que sans les outils.

Mathématiques formelles

L'ensemble de données AlgebraicStack de

Proof-Pile-2 contient 1,5 milliard de jetons de données mathématiques formelles, y compris des preuves formelles extraites de Lean et Isabelle. Bien qu’une étude complète des mathématiques formelles dépasse le cadre de cet article, nous avons évalué les performances en quelques coups de LLEMMA sur les deux tâches suivantes.

Tâche de preuve informelle à formelle, c'est-à-dire, étant donné une proposition formelle, une proposition informelle LATEX et une preuve LATEX informelle, générer une preuve formelle

Formulaire à une tâche de preuve formelle, c'est-à-dire ; , pour prouver une proposition formelle en générant une série d'étapes de preuve (ou stratégies).

Les résultats sont présentés dans le tableau 4 ci-dessous. La pré-formation continue de LLEMMA sur Proof-Pile-2 a amélioré les performances de quelques échantillons sur deux tâches formelles de preuve de théorème.

Impact du mélange de données

Lors de la formation d'un modèle de langage, une pratique courante consiste à suréchantillonner un sous-ensemble de haute qualité des données d'entraînement en fonction du mélange de poids. Les chercheurs ont sélectionné les poids de mélange en effectuant une courte formation sur plusieurs poids de mélange soigneusement sélectionnés. Des poids mixtes ont ensuite été sélectionnés pour minimiser la perplexité sur un ensemble de textes retenus de haute qualité (ici, l'ensemble de formation MATH a été utilisé).

Le tableau 5 ci-dessous montre la perplexité de l'ensemble d'entraînement MATH du modèle après un entraînement avec différents mélanges de données tels que arXiv, web et code.

Pour plus de détails techniques et les résultats de l'évaluation, veuillez vous référer à l'article original.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!