
En machine learning, le terme ensemble fait référence à la combinaison de plusieurs modèles en parallèle, l'idée est d'utiliser la sagesse de la foule pour former un meilleur consensus sur la réponse finale donnée.

Dans le domaine de l'apprentissage supervisé, cette méthode a été largement étudiée et appliquée, notamment dans les problèmes de classification avec des algorithmes très performants comme RandomForest. Un système de vote/pondération est souvent utilisé pour combiner les résultats de chaque modèle individuel en un résultat final plus robuste et cohérent.
Dans le monde de l'apprentissage non supervisé, cette tâche devient plus difficile. Premièrement, parce que cela englobe les défis du domaine lui-même, nous n’avons aucune connaissance préalable des données pour nous comparer à une cible. Deuxièmement, parce que trouver un moyen approprié de combiner les informations de tous les modèles reste un problème, et il n’existe pas de consensus sur la manière d’y parvenir.
Dans cet article, nous discutons de la meilleure approche sur ce sujet, à savoir le clustering de matrices de similarité.
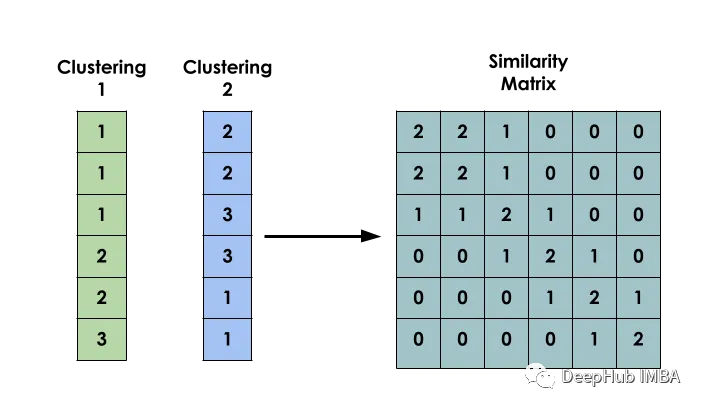
L'idée principale de cette méthode est la suivante : étant donné un ensemble de données X, créer une matrice S telle que Si représente la similarité entre xi et xj. Cette matrice est construite sur la base des résultats de clustering de plusieurs modèles différents.
Créer une matrice de cooccurrence binaire entre les entrées est la première étape de la construction d'un modèle

Elle est utilisée pour indiquer si deux entrées i et j appartiennent au même cluster.
import numpy as np from scipy import sparse def build_binary_matrix( clabels ): data_len = len(clabels) matrix=np.zeros((data_len,data_len))for i in range(data_len):matrix[i,:] = clabels == clabels[i]return matrix labels = np.array( [1,1,1,2,3,3,2,4] ) build_binary_matrix(labels)
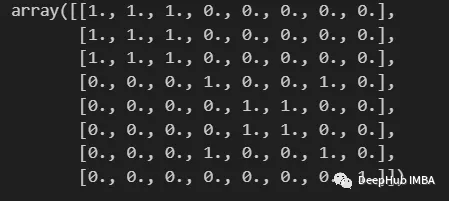
Nous avons construit une fonction pour binariser nos clusters, et nous pouvons maintenant entrer dans l'étape de construction de la matrice de similarité.
Nous introduisons ici une méthode courante, qui consiste uniquement à calculer la valeur moyenne entre M matrices de cooccurrence générées par M modèles différents. Nous le définissons comme :

Lorsque les éléments appartiennent au même cluster, leur valeur de similarité sera proche de 1, et lorsque les éléments appartiennent à des groupes différents, leur valeur de similarité sera proche de 0
Nous construirons une similarité matrice basée sur les étiquettes créées par le modèle K-Means. Réalisé à l’aide de l’ensemble de données MNIST. Pour des raisons de simplicité et d'efficacité, nous n'utiliserons que 10 000 images réduites en PCA.
from sklearn.datasets import fetch_openml from sklearn.decomposition import PCA from sklearn.cluster import MiniBatchKMeans, KMeans from sklearn.model_selection import train_test_split mnist = fetch_openml('mnist_784') X = mnist.data y = mnist.target X, _, y, _ = train_test_split(X,y, train_size=10000, stratify=y, random_state=42 ) pca = PCA(n_components=0.99) X_pca = pca.fit_transform(X)Pour permettre la diversité entre les modèles, chaque modèle est instancié avec un nombre aléatoire de clusters.
NUM_MODELS = 500 MIN_N_CLUSTERS = 2 MAX_N_CLUSTERS = 300 np.random.seed(214) model_sizes = np.random.randint(MIN_N_CLUSTERS, MAX_N_CLUSTERS+1, size=NUM_MODELS) clt_models = [KMeans(n_clusters=i, n_init=4, random_state=214) for i in model_sizes] for i, model in enumerate(clt_models):print( f"Fitting - {i+1}/{NUM_MODELS}" )model.fit(X_pca)La fonction suivante consiste à créer une matrice de similarité
def build_similarity_matrix( models_labels ):n_runs, n_data = models_labels.shape[0], models_labels.shape[1] sim_matrix = np.zeros( (n_data, n_data) ) for i in range(n_runs):sim_matrix += build_binary_matrix( models_labels[i,:] ) sim_matrix = sim_matrix/n_runs return sim_matrix
Appelez cette fonction :
models_labels = np.array([ model.labels_ for model in clt_models ]) sim_matrix = build_similarity_matrix(models_labels)
Le résultat final est le suivant :
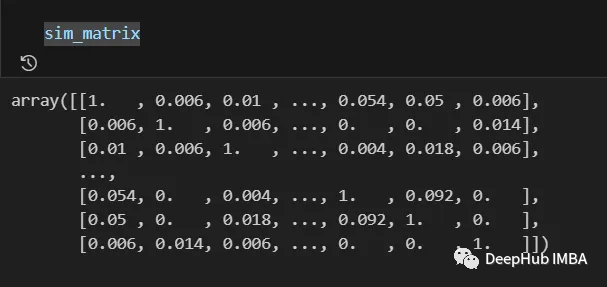
Les informations de la matrice de similarité peuvent toujours être post-traitées avant la dernière étape , comme l'application de logarithmes, de polynômes Attendez la transformation.
Dans notre cas, nous garderons le sens original inchangé et réécrirons
Pos_sim_matrix = sim_matrix
La matrice de similarité est un moyen de représenter les connaissances construites par la collaboration de tous les modèles de clustering.
Nous pouvons l'utiliser pour voir visuellement quelles entrées sont les plus susceptibles d'appartenir au même cluster et lesquelles ne le sont pas. Cependant, ces informations doivent encore être converties en clusters réels
Cela se fait en utilisant un algorithme de clustering qui peut recevoir une matrice de similarité en tant que paramètre. Ici, nous utilisons SpectralClustering.
from sklearn.cluster import SpectralClustering spec_clt = SpectralClustering(n_clusters=10, affinity='precomputed',n_init=5, random_state=214) final_labels = spec_clt.fit_predict(pos_sim_matrix)
Comparons-le avec KMeans pour confirmer si notre méthode est efficace.
Nous utiliserons les indicateurs NMI, ARI, de pureté de cluster et de pureté de classe pour évaluer le modèle KMeans standard et comparer avec notre modèle d'ensemble. De plus, nous tracerons la matrice de contingence pour visualiser quelles catégories appartiennent à chaque cluster
from seaborn import heatmap import matplotlib.pyplot as plt def data_contingency_matrix(true_labels, pred_labels): fig, (ax) = plt.subplots(1, 1, figsize=(8,8)) n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels)label_names.sort() contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) heatmap(contingency_matrix.astype(int), ax=ax,annot=True, annot_kws={"fontsize":14}, fmt='d') ax.set_xlabel("Clusters", fontsize=18)ax.set_xticks( [i+0.5 for i in range(n_clusters)] )ax.set_xticklabels([i for i in range(n_clusters)], fontsize=14) ax.set_ylabel("Original classes", fontsize=18)ax.set_yticks( [i+0.5 for i in range(n_classes)] )ax.set_yticklabels(label_names, fontsize=14, va="center") ax.set_title("Contingency Matrix\n", ha='center', fontsize=20)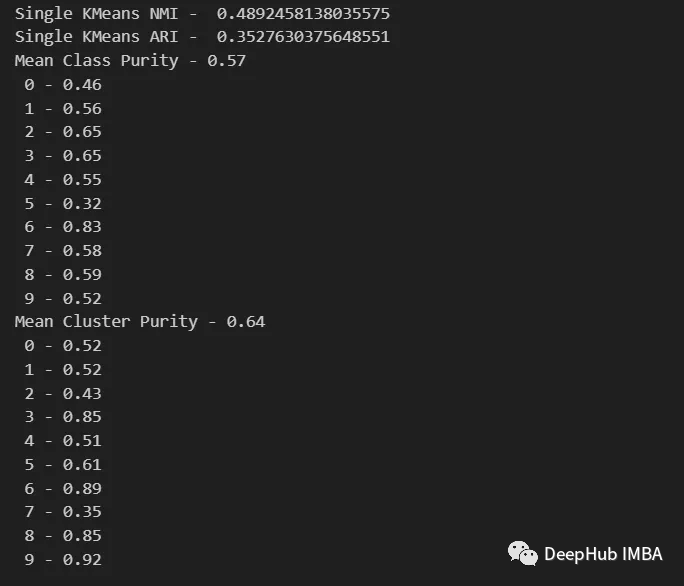
from sklearn.metrics import normalized_mutual_info_score, adjusted_rand_score def purity( true_labels, pred_labels ): n_clusters = len(np.unique(pred_labels))n_classes = len(np.unique(true_labels))label_names = np.unique(true_labels) purity_vector = np.zeros( (n_classes) )contingency_matrix = np.zeros( (n_classes, n_clusters) ) for i, true_label in enumerate(label_names):for j in range(n_clusters):contingency_matrix[i, j] = np.sum(np.logical_and(pred_labels==j, true_labels==true_label)) purity_vector = np.max(contingency_matrix, axis=1)/np.sum(contingency_matrix, axis=1) print( f"Mean Class Purity - {np.mean(purity_vector):.2f}" ) for i, true_label in enumerate(label_names):print( f" {true_label} - {purity_vector[i]:.2f}" ) cluster_purity_vector = np.zeros( (n_clusters) )cluster_purity_vector = np.max(contingency_matrix, axis=0)/np.sum(contingency_matrix, axis=0) print( f"Mean Cluster Purity - {np.mean(cluster_purity_vector):.2f}" ) for i in range(n_clusters):print( f" {i} - {cluster_purity_vector[i]:.2f}" ) kmeans_model = KMeans(10, n_init=50, random_state=214) km_labels = kmeans_model.fit_predict(X_pca) data_contingency_matrix(y, km_labels) print( "Single KMeans NMI - ", normalized_mutual_info_score(y, km_labels) ) print( "Single KMeans ARI - ", adjusted_rand_score(y, km_labels) ) purity(y, km_labels)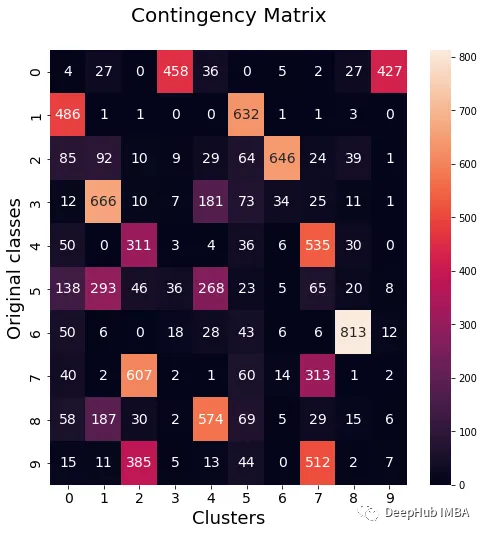
data_contingency_matrix(y, final_labels) print( "Ensamble NMI - ", normalized_mutual_info_score(y, final_labels) ) print( "Ensamble ARI - ", adjusted_rand_score(y, final_labels) ) purity(y, final_labels)
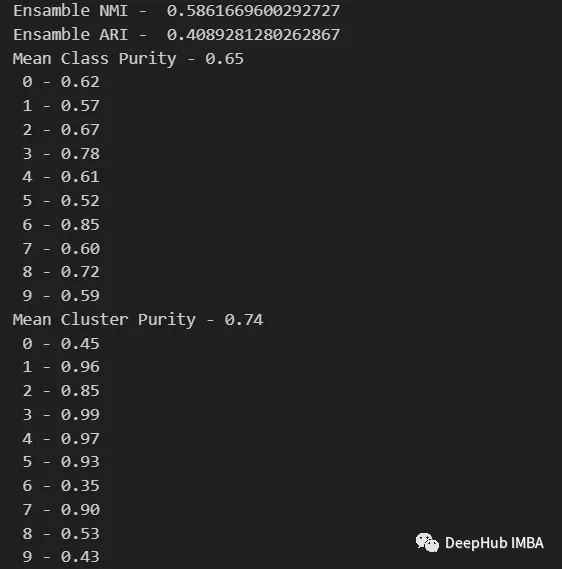
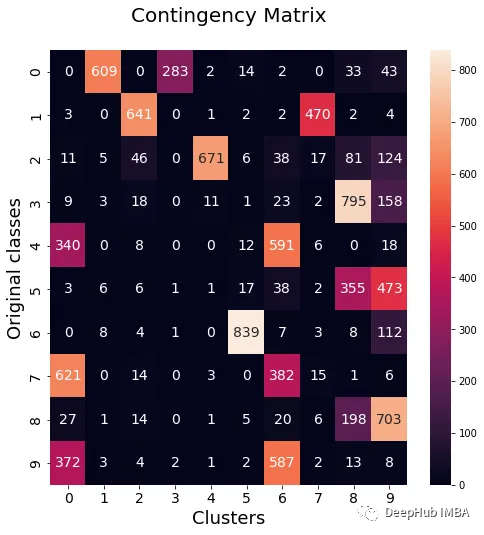
En observant les valeurs ci-dessus, il apparaît clairement que la méthode Ensemble peut améliorer efficacement la qualité du clustering. Dans le même temps, un comportement plus cohérent peut également être observé dans la matrice de contingence, avec de meilleures catégories de répartition et moins de « bruit »
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Quelle est la différence entre golang et python
Quelle est la différence entre golang et python
 Quelle est la priorité de l'interruption ?
Quelle est la priorité de l'interruption ?
 diablotin oracle
diablotin oracle
 Comment illuminer le moment des amis proches de Douyin
Comment illuminer le moment des amis proches de Douyin
 Comment définir les numéros de page dans Word
Comment définir les numéros de page dans Word
 Utilisation de #include en langage C
Utilisation de #include en langage C
 Utilisation de la commande source sous Linux
Utilisation de la commande source sous Linux
 Le rôle du routeur
Le rôle du routeur