
Les mathématiques, en tant que pierre angulaire de la science, ont toujours été un domaine clé de recherche et d'innovation.
Récemment, sept institutions, dont l'Université de Princeton, ont publié conjointement un grand modèle de langage LLEMMA spécifiquement pour les mathématiques, avec des performances comparables à celles de Google Minerva 62B, et ont rendu public son modèle, son ensemble de données et son code, apportant des avantages sans précédent aux opportunités de recherche en mathématiques. ressources.

Adresse papier : https://arxiv.org/abs/2310.10631
L'adresse du lien de l'ensemble de données est : https://huggingface.co/datasets/EleutherAI/proof-pile- 2
Adresse du projet : https://github.com/EleutherAI/math-lm Ce qui doit être réécrit, c'est :
LLEMMA hérite des fondations de Code Llama et est pré-entraînée sur Proof-Pile-2.
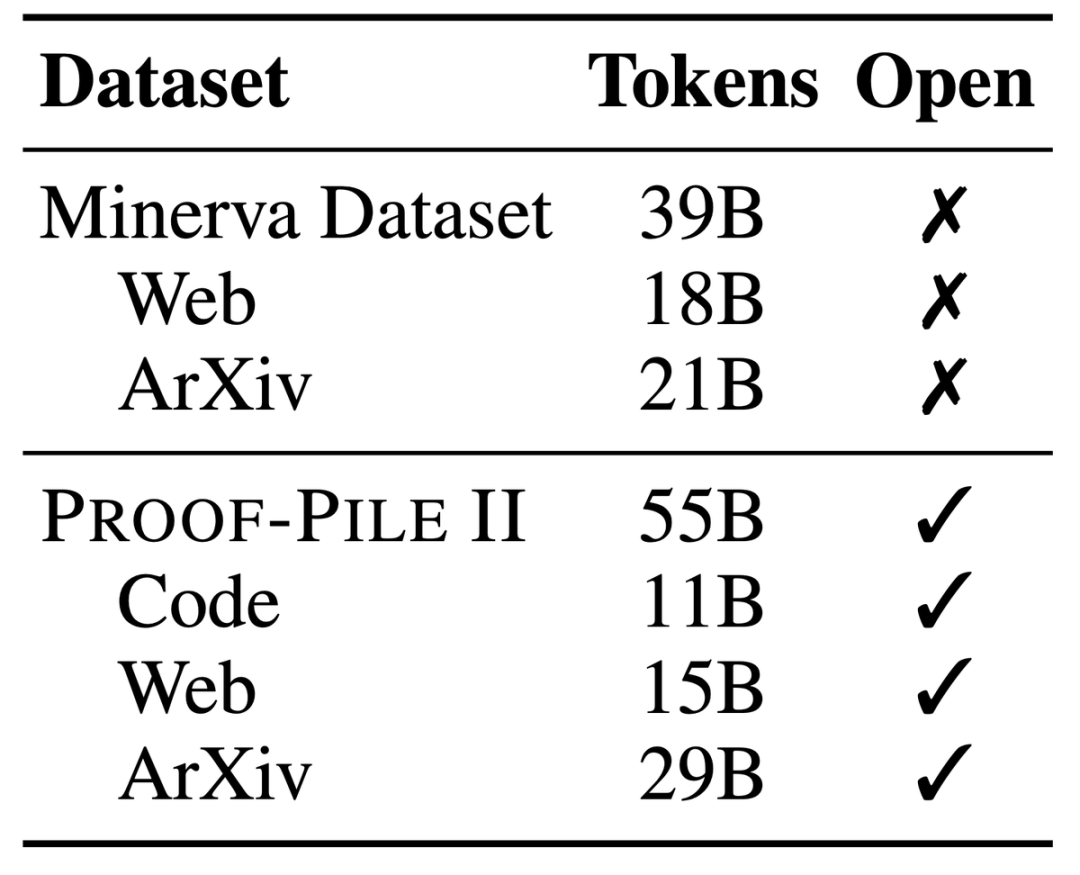
Proof-Pile-2, un énorme ensemble de données mixtes contenant des informations de 55 milliards de jetons, notamment des articles scientifiques, des données Web riches en contenu mathématique et des codes mathématiques.
Une partie de cet ensemble de données, la pile algébrique, rassemble 11 milliards d'ensembles de données provenant de 17 langues, couvrant des preuves numériques, symboliques et mathématiques.
Avec 700 millions et 3,4 milliards de paramètres, il fonctionne extrêmement bien dans le benchmark MATH, surpassant tous les modèles de base open source connus.
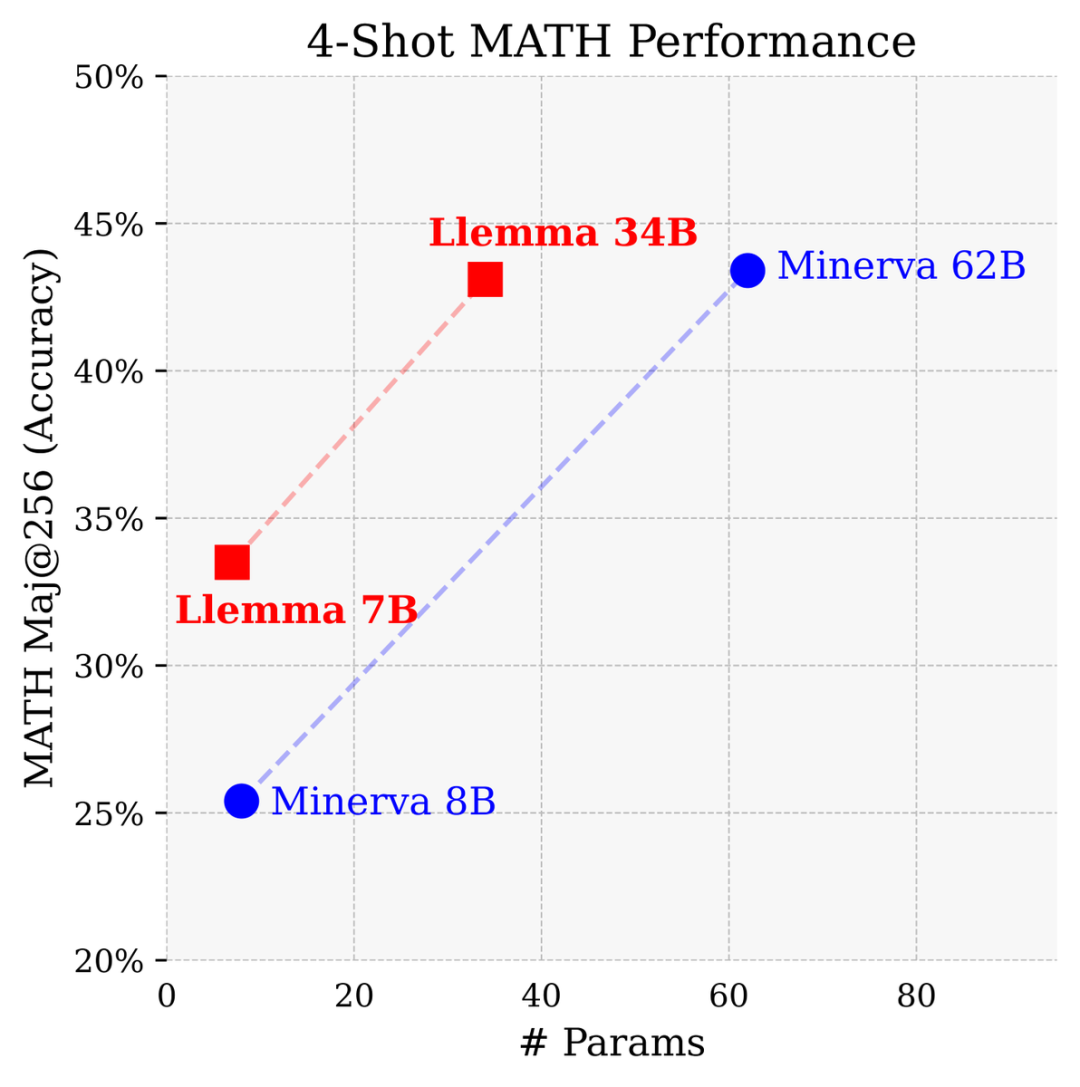
Comparé à un modèle fermé développé par Google Research spécifiquement pour les mathématiques, le Llemme 34B a atteint presque les mêmes performances avec la moitié du nombre de paramètres du Minerva 62B.
Llemma surpasse les performances de Minerva dans la résolution de problèmes sur la base de paramètres. Il utilise des outils informatiques et des preuves de théorèmes formels pour offrir des possibilités illimitées de résolution de problèmes mathématiques
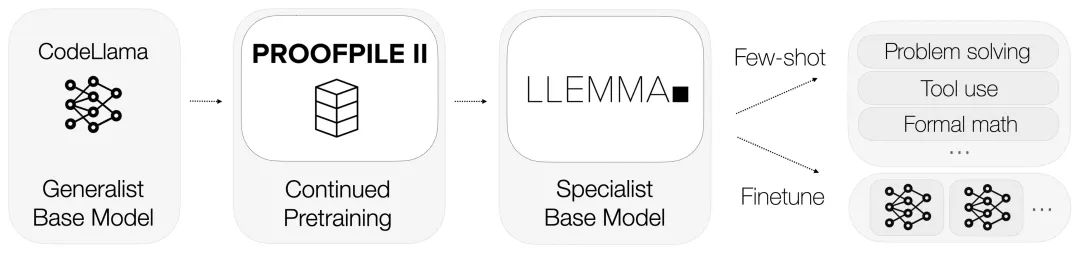
Il peut facilement utiliser un interpréteur Python et un prouveur formel, en outre. démontrant sa capacité à résoudre des problèmes mathématiques
En raison de l'accent particulier mis sur les données de preuve formelle, Algebraic Stack est devenu le premier open source à démontrer la capacité de prouver des théorèmes en quelques coups Modèle de base

 Photo
Photo
Les chercheurs ont également partagé ouvertement toutes les données et le code de formation de LLEMMA. Différent des modèles mathématiques précédents, LLEMMA est un modèle open source, ouvert et partagé, ouvrant la porte à l’ensemble de la communauté de la recherche scientifique.
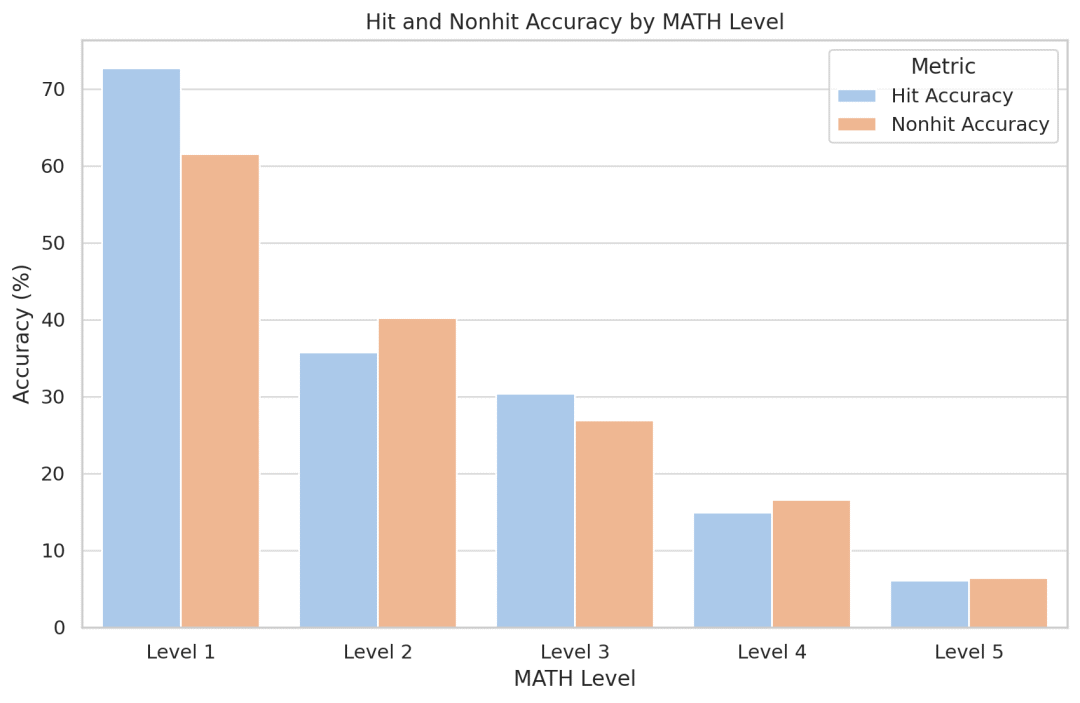
Les chercheurs ont tenté de quantifier l'effet mémoire du modèle et, étonnamment, ils ont constaté que Llemma ne devenait pas plus précis pour les problèmes apparus dans l'ensemble d'entraînement. Puisque le code et les données sont accessibles au public, les chercheurs encouragent les autres à reproduire et étendre leur analyse
LLEMMA est un grand modèle de langage dédié aux mathématiques, qui continue d'être pré-entraîné sur Proof-Pile-2 basé sur Code Llama. Proof-Pile-2 est un ensemble de données mixtes contenant des articles scientifiques, des données de pages Web à contenu mathématique et du code mathématique. Il contient 55 milliards de balises. La partie code d'AlgebraicStack contient 11 milliards d'ensembles de données, dont 17 types. couvrant les mathématiques numériques, symboliques et formelles, est rendu public
Chaque modèle de LLEMMA est initialisé par Code Llama. Le modèle Code Llama est un modèle de langage uniquement décodeur qui est initialisé à partir de Llama 2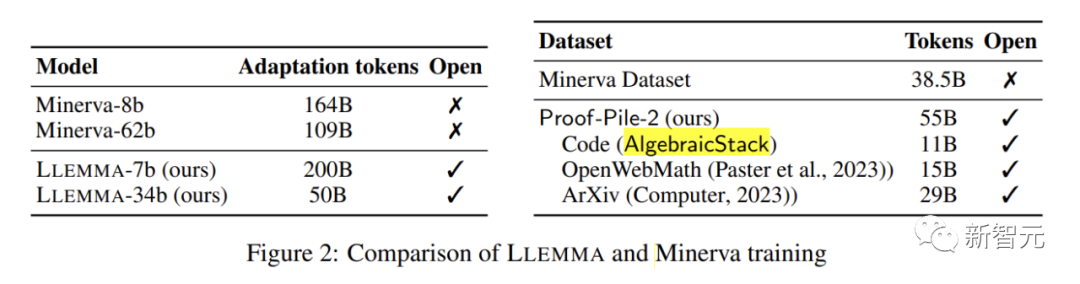
L'auteur a ensuite formé le modèle Code Llama sur Proof-Pile-2, en utilisant la cible de modèle de construction de langage autorégressif standard. Pour le modèle 7B, l'auteur a effectué un entraînement avec des marqueurs 200B, tandis que pour le modèle 34B, l'auteur a effectué un entraînement avec des marqueurs 50B
Méthodes d'évaluation et résultats expérimentaux
Les chercheurs ont constaté que LLEMMA s'était considérablement amélioré dans ces tâches et était capable de s'adapter à différents types de problèmes et difficultés.
LLEMMA 34B démontre des capacités mathématiques plus puissantes que les autres modèles de base ouverts dans des problèmes mathématiques extrêmement difficiles
Sur les benchmarks mathématiques, LLEMMA continue de surperformer sur Proof-Pile-2 Le pré-entraînement améliore les performances en quelques coups sur cinq tests mathématiques. 
L'amélioration de LLEMMA 34B est de 20 points de pourcentage supérieure à celle de Code Llama sur GSM8k et de 13 points de pourcentage supérieure sur MATH. De plus, LLEMMA 7B surpasse également le modèle propriétaire Minerva de taille similaire, ce qui prouve que la pré-formation sur Proof-Pile-2 peut améliorer efficacement la capacité de résolution de problèmes mathématiques des grands modèles
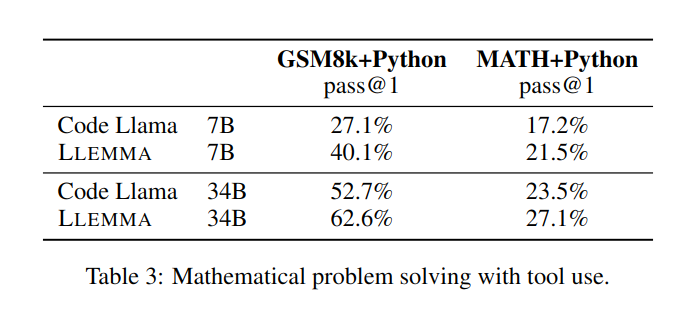
dans la résolution de problèmes mathématiques. en utilisant des outils informatiques tels que Python, LLEMMA fonctionne mieux que Code Llama sur les tâches MATH+Python et GSM8k+Python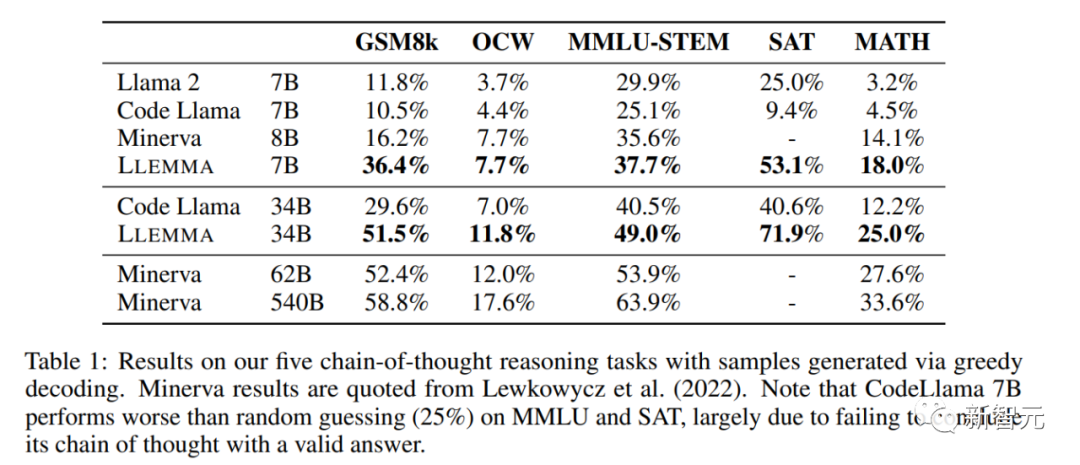
Lors de l'utilisation d'ensembles de données MATH et GSM8k, les performances de LLEMMA sont meilleures que les performances sans utiliser d'outils
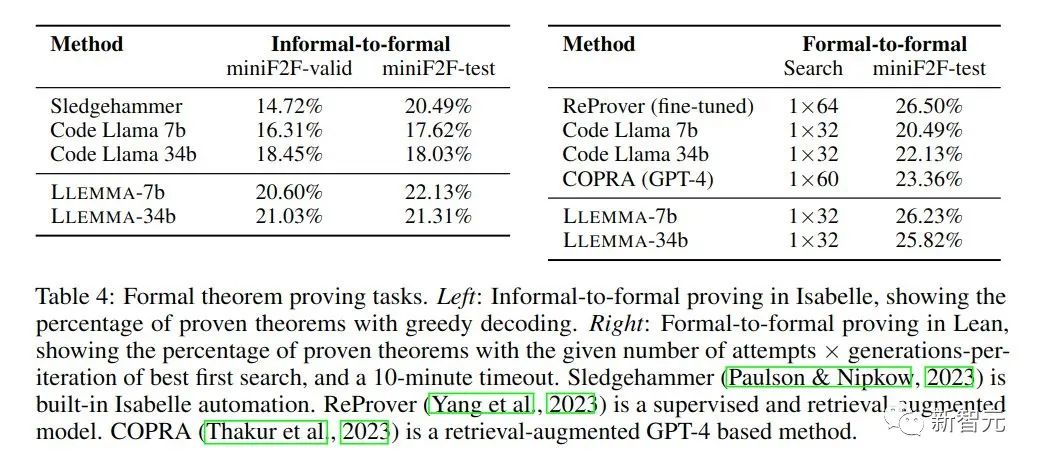
Dans les tâches de preuve mathématique, LLEMMA fonctionne bien 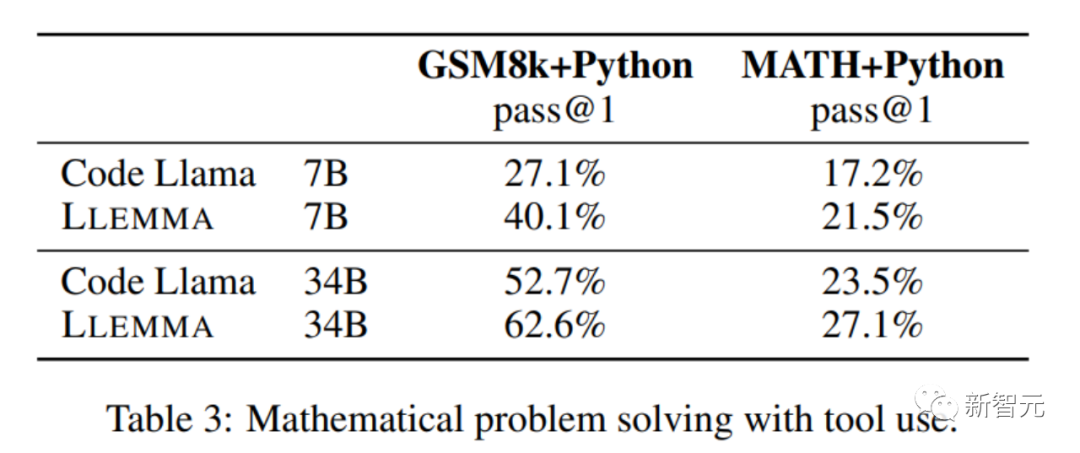
L'objectif de la tâche de preuve informelle à formelle reçoit une instruction formelle, une instruction LATEX informelle et une preuve LATEX informelle. Dans ce cas, une preuve formelle est générée. puis vérifié par un assistant de preuve.
La preuve formelle à formelle consiste à prouver une déclaration formelle en générant une série d'étapes de preuve (stratégies). Les résultats montrent que la pré-formation continue de LLEMMA sur Proof-Pile-2 améliore les performances en quelques tirs de ces deux tâches formelles de preuve de théorèmes.
LLEMMA a non seulement des performances impressionnantes, mais ouvre également des ensembles de données révolutionnaires et démontre d'étonnantes capacités de résolution de problèmes. 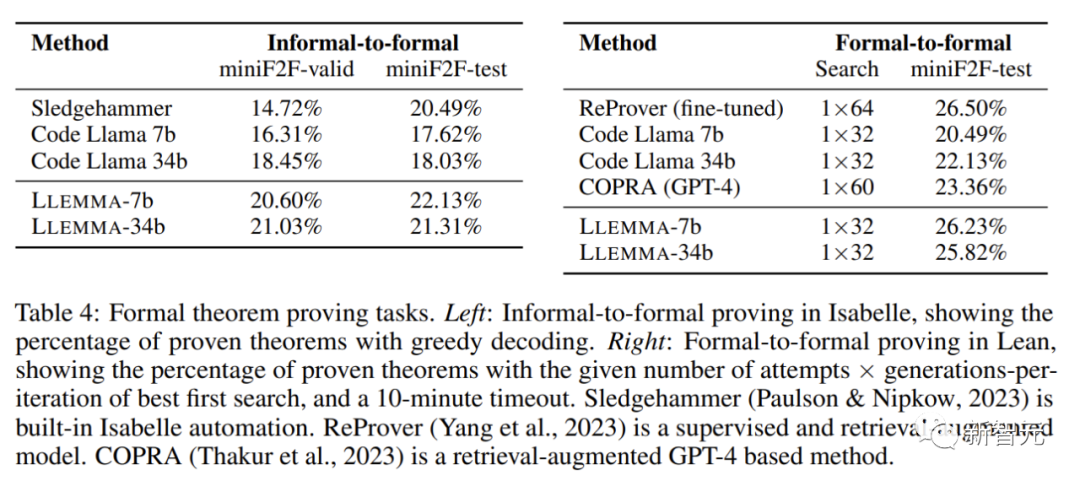
L'esprit du partage open source marque une nouvelle ère dans le monde des mathématiques. L’avenir des mathématiques est là, et chacun d’entre nous, passionnés de mathématiques, chercheurs et éducateurs, en bénéficiera.
L'émergence de LLEMMA nous offre des outils sans précédent pour rendre la résolution de problèmes mathématiques plus efficace et innovante.
En outre, le concept de partage ouvert favorisera également une coopération plus approfondie au sein de la communauté mondiale de la recherche scientifique et promouvra conjointement le progrès scientifique.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Comment lier des données dans une liste déroulante
Comment lier des données dans une liste déroulante
 Que faire en cas de conflit IP
Que faire en cas de conflit IP
 Logiciel de système de gestion immobilière
Logiciel de système de gestion immobilière
 Quelles sont les méthodes pour changer le mot de passe dans MySQL ?
Quelles sont les méthodes pour changer le mot de passe dans MySQL ?
 ERR_CONNECTION_REFUSED
ERR_CONNECTION_REFUSED
 Introduction aux types d'interfaces de disque dur
Introduction aux types d'interfaces de disque dur
 Site officiel de l'application de plateforme de trading okex
Site officiel de l'application de plateforme de trading okex
 Que faire si la visionneuse de photos Windows manque de mémoire
Que faire si la visionneuse de photos Windows manque de mémoire