Périphériques technologiques
IA
11 distributions de base que les data scientists utilisent 95 % du temps
11 distributions de base que les data scientists utilisent 95 % du temps
Suite au dernier inventaire des "11 graphiques de base utilisés par les data scientists 95% du temps", nous vous présenterons aujourd'hui 11 distributions de base que les data scientists utilisent 95% du temps. La maîtrise de ces distributions nous aide à comprendre plus profondément la nature des données et à faire des inférences et des prédictions plus précises lors de l'analyse des données et de la prise de décision.
1. Distribution normale
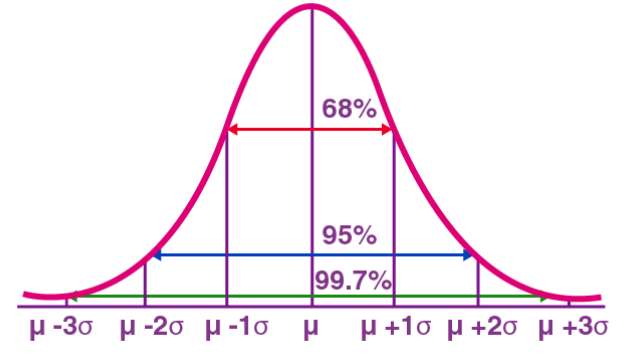
La distribution normale, également connue sous le nom de distribution gaussienne, est une distribution de probabilité continue. Il présente une courbe symétrique en forme de cloche avec la moyenne (μ) comme centre et l'écart type (σ) comme largeur. La distribution normale a une valeur d'application importante dans de nombreux domaines tels que les statistiques, la théorie des probabilités et l'ingénierie.
La fonction de densité de probabilité de la distribution normale peut être exprimée comme suit :
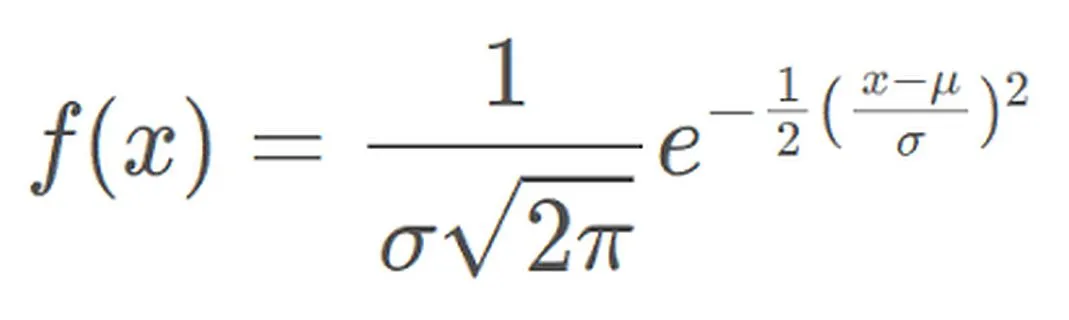
La fonction de densité de probabilité représente la densité de probabilité des valeurs d'une variable aléatoire normalement distribuée dans l'intervalle unitaire près d'une valeur donnée X. Parmi eux, μ représente la moyenne et σ représente l'écart type. La distribution normale est largement utilisée dans la pratique. Par exemple, la distribution de la taille et du poids humains se rapproche d’une distribution normale. En outre, les résultats des tests sont souvent distribués normalement, avec moins de personnes ayant des scores élevés et faibles et davantage de personnes ayant des scores moyens. Ce modèle de distribution a une valeur d'application importante dans de nombreux domaines
2. La distribution de Bernoulli
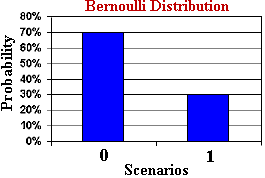
La distribution de Bernoulli (distribution de Bernoulli) est une distribution de probabilité discrète utilisée pour décrire un seul événement avec seulement deux résultats possibles. Les essais de Bernoulli peuvent être pile ou face, succès ou échec, oui ou non, etc. Par exemple, lancer une pièce de monnaie, tester si un produit est qualifié, si quelqu'un achète un certain produit, etc.
La fonction de masse de probabilité de la distribution de Bernoulli est :
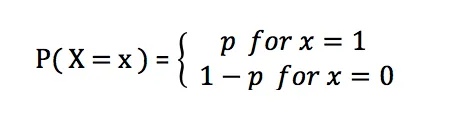Dans la distribution de Bernoulli, p représente la probabilité de succès et sa valeur varie de 0 à 1. Lorsque p est égal à 0,5, la distribution de Bernoulli se rapproche d'une distribution uniforme
Application de la distribution de Bernoulli en pratique : Par exemple, la distribution binomiale est n expériences répétées indépendantes de la distribution de Bernoulli.
3. Distribution binomiale
La distribution binomiale (distribution binomiale) est une distribution de probabilité discrète utilisée pour décrire la distribution de probabilité du nombre de réussites dans n expériences répétées indépendantes. Chaque essai n'a que deux résultats possibles : le succès (enregistré comme 1) ou l'échec (enregistré comme 0). La probabilité de succès est p et la probabilité d’échec est 1-p.
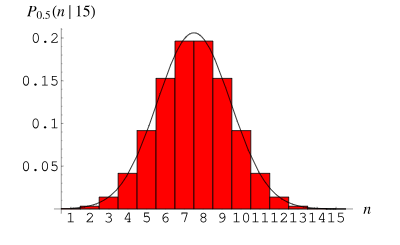La fonction de masse de probabilité de la distribution binomiale peut être exprimée comme suit :
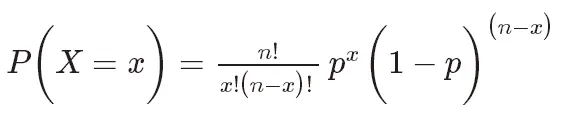où, P(X=k) représente la probabilité de k fois de réussite,
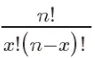La distribution binomiale est largement utilisée dans la pratique. Par exemple, dans la recherche médicale, nous pouvons utiliser la distribution binomiale pour calculer le taux de réussite d’un patient recevant un certain traitement. Dans le domaine de l'ingénierie, on peut utiliser la distribution binomiale pour évaluer le taux de qualification d'un produit au cours du processus de production. Ce sont des exemples importants de distribution binomiale dans des applications pratiques
4. La distribution de Poisson
La distribution de Poisson (distribution de Poisson) est une distribution de probabilité discrète utilisée pour décrire le nombre d'événements qui se produisent dans une période de temps fixe. La distribution de Poisson convient aux situations où les événements sont indépendants et se produisent à un rythme moyen constant.
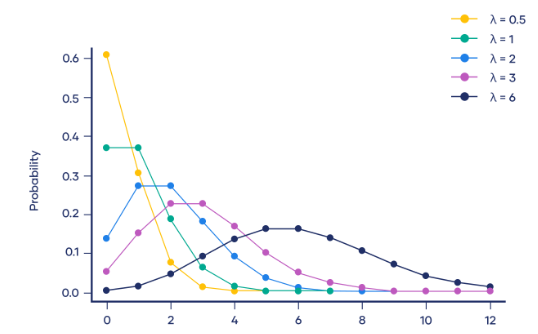La fonction de densité de probabilité de la distribution de Poisson est :
Ici, P(X=k) représente la probabilité qu'un événement se produise k fois dans une période de temps fixe, et λ représente le taux d'occurrence moyen d'un événement, qui est le nombre moyen d'événements se produisant par unité de temps. e est une constante naturelle, approximativement égale à 2,718. k représente le nombre d'événements qui se produisent. La distribution de Poisson est largement utilisée dans la pratique. Par exemple, dans un centre d'appels, le nombre d'appels par minute peut être considéré comme une distribution de Poisson, où le nombre moyen d'appels par minute est λ
.5. Distribution exponentielle
La distribution exponentielle (distribution exponentielle) est une distribution de probabilité continue utilisée pour décrire la probabilité qu'un événement se produise dans un temps fixe. La distribution exponentielle convient aux situations dans lesquelles les événements sont indépendants les uns des autres et se produisent à un rythme moyen constant.
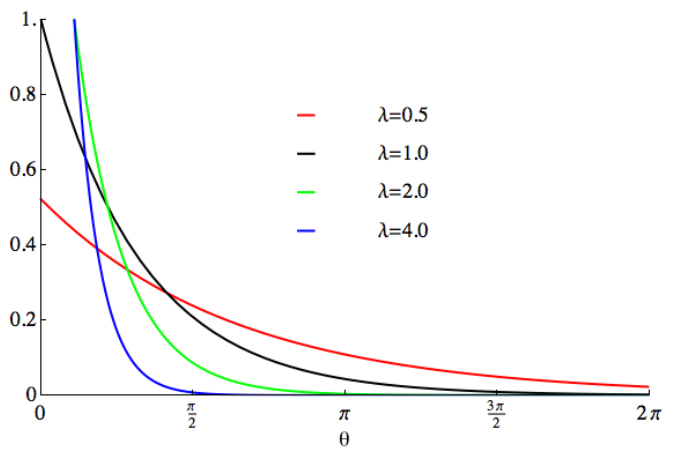La fonction de densité de probabilité de la distribution exponentielle est :
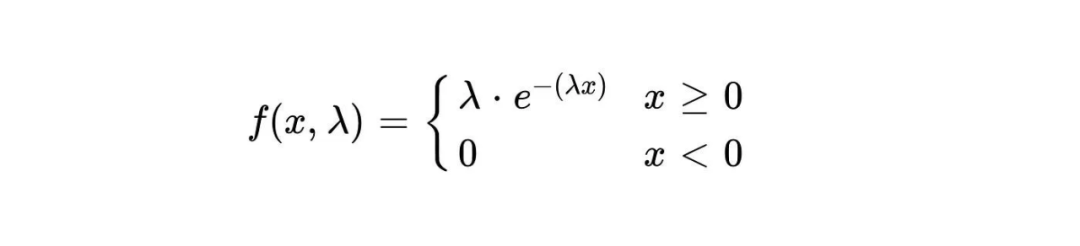La densité de probabilité d'un événement se produisant dans un temps donné x est représentée par f(x,λ). λ représente le taux d'occurrence moyen des événements, c'est-à-dire le nombre moyen d'événements se produisant par unité de temps. e est une constante naturelle, approximativement égale à 2,718
La distribution exponentielle a de nombreuses applications dans la vie réelle. Par exemple, dans la désintégration radioactive, les temps de désintégration des noyaux radioactifs peuvent être considérés comme distribués de manière exponentielle. Cela signifie que la distribution de probabilité des temps de décroissance suit une fonction exponentielle. Le temps de décroissance moyen correspond au paramètre λ de la fonction exponentielle
6. Distribution gamma
La distribution gamma est une distribution de probabilité continue utilisée pour décrire la probabilité qu'un événement se produise dans un temps donné. Cela s'applique à la situation où les événements sont indépendants les uns des autres et le taux d'occurrence moyen est toujours constant. La fonction de densité de probabilité de la distribution gamma est :
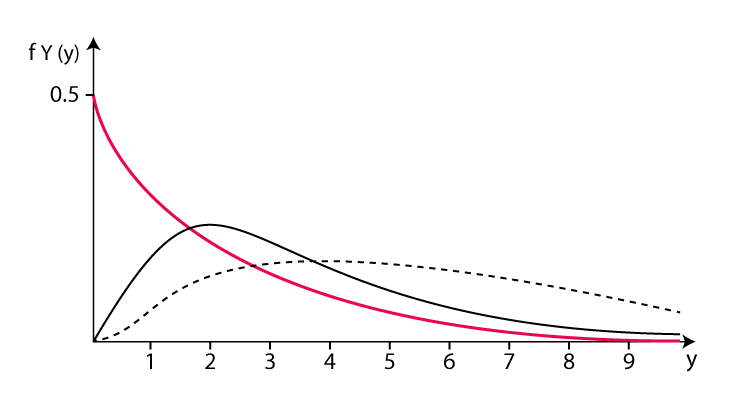où f(x) représente le temps x à un instant précis. densité de probabilité des événements internes. α et β sont les paramètres de forme et les paramètres de taux de la distribution gamma. α est utilisé pour déterminer la forme de la distribution gamma et sa valeur va de 0 à l’infini positif. β représente le taux d'occurrence moyen des événements, c'est-à-dire le nombre moyen d'événements se produisant par unité de temps, et la plage de valeurs va de 0 à l'infini positif. e est une constante naturelle, approximativement égale à 2,718. Applications pratiques de la distribution gamma : Par exemple, désintégration radioactive : Dans la désintégration radioactive, le temps nécessaire à la désintégration des noyaux radioactifs peut être considéré comme une distribution gamma, et le temps de désintégration moyen est β/. α.
7. Distribution bêta
La distribution bêta est une distribution de probabilité continue qui est utilisée pour décrire la distribution de probabilité du nombre de succès dans un ensemble de valeurs. Il comporte deux paramètres, représentant la valeur attendue (moyenne) et l'écart type (écart type) de la probabilité de succès.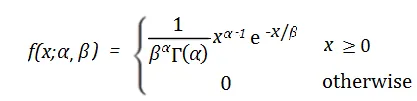 
La fonction de densité de probabilité de la distribution bêta est la suivante :
En cela, x représente le nombre de succès, α et β représentent respectivement les paramètres de forme de la distribution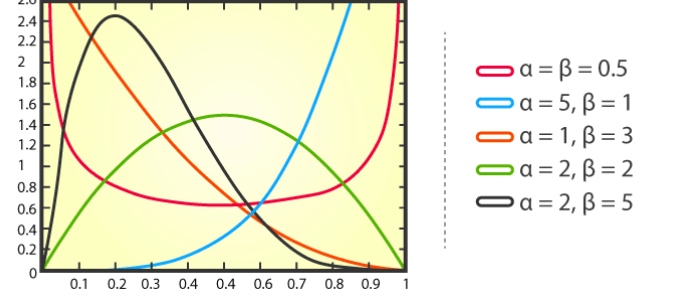
La distribution bêta a des applications dans de nombreux problèmes pratiques. Par exemple, dans le domaine de l’édition génétique, les chercheurs peuvent utiliser une distribution bêta pour prédire la probabilité qu’une technologie d’édition génétique parvienne à modifier un certain site cible. Dans le domaine financier, la distribution bêta peut être utilisée pour décrire la volatilité des prix des actifs ou pour calculer le rendement attendu d'un portefeuille d'investissement
8 Distribution uniforme
La distribution uniforme est une distribution de probabilité utilisée pour décrire un ensemble. de valeurs dans un certain uniformément réparties dans l'intervalle. Il existe deux types de distributions uniformes : la distribution uniforme discrète et la distribution uniforme continue.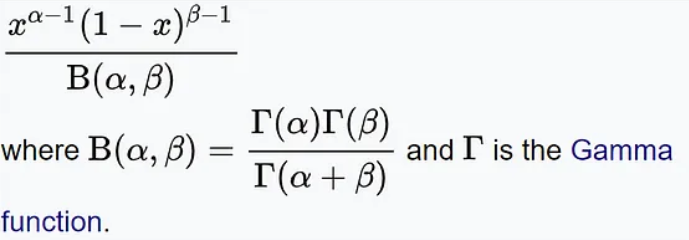 
9. Distribution log-normale
La distribution log-normale (Distribution Log-normale) est une distribution de probabilité continue, qui est caractérisée par le logarithme de la variable aléatoire obéissant à la distribution normale. En d’autres termes, si le logarithme ln(X) d’une variable aléatoire X obéit à la distribution normale, alors la variable aléatoire X obéit à la distribution lognormale.
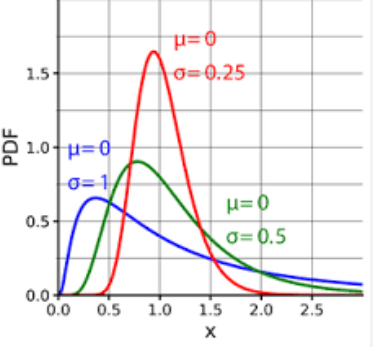
La fonction de densité de probabilité de la distribution lognormale peut être exprimée comme suit :
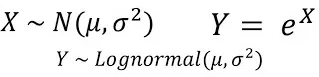
où μ est la moyenne de la distribution lognormale et σ est l'écart type de la distribution lognormale.
La distribution lognormale revêt une grande importance dans de nombreuses applications pratiques, telles que la finance (cours des actions, rendements, etc.), la biologie (taux de croissance, etc.), l'économie (dépenses de consommation, etc.), etc.
10. Distribution T
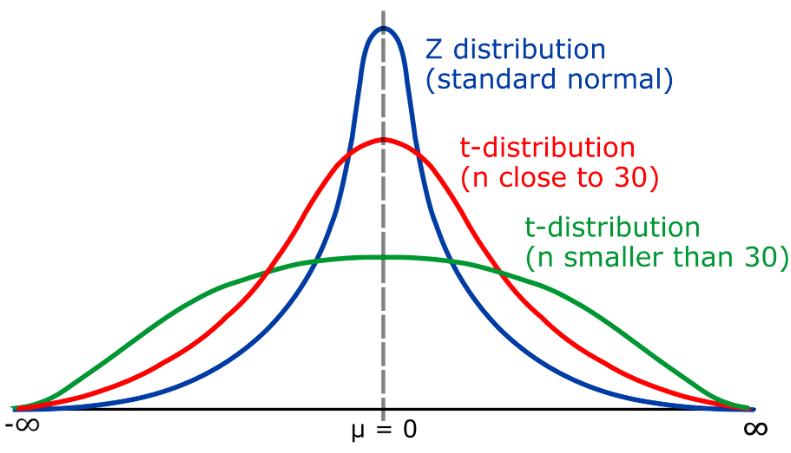
La distribution T est une distribution de probabilité continue, qui est principalement utilisée pour décrire la distribution de la moyenne dans le cas de petits échantillons. La distribution t est similaire à la distribution normale, mais sa queue peut s'étendre vers la gauche et la droite, en fonction du degré de liberté (k). La distribution t est largement utilisée dans l'inférence statistique, comme dans les tests d'hypothèses pour évaluer la différence significative entre la moyenne de l'échantillon et la moyenne de la population.
L'espérance et la variance de la distribution t sont les suivantes :
E(t)=0
Le contenu à réécrire est : Var(t)=k/(k-1)
Les degrés de la distribution de liberté de t (k) représente la relation entre la taille de l'échantillon (n) et l'écart type de la population. Lorsque k > 30, la distribution t est proche de la distribution normale ; lorsque k est proche de 1, la distribution t devient la distribution de Cauchy (distribution de Cauchy)
Dans les applications pratiques, lorsque la taille de l'échantillon est grande (n>30) , cela peut Le test d'hypothèse est effectué en utilisant la distribution normale. Dans ce cas, la statistique z peut être utilisée pour établir un intervalle de confiance. Cependant, lorsque la taille de l'échantillon est petite (n
11. Distribution de Weibull
La distribution de Weibull (distribution de Weibull) est une distribution de probabilité continue.
La fonction de densité de probabilité de la distribution de Weibull est :
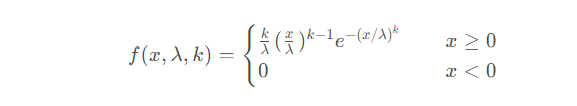
Dans la distribution de Weibull, x est considéré comme une variable aléatoire, λ est appelé le paramètre d'échelle (échelle) et k est le paramètre de forme (forme). En ce qui concerne la distribution de Weber, lorsque k est égal à 1, il s'agit d'une distribution exponentielle. Si λ est égal à 1, c'est la distribution de Weber minimisée
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Outils d'IA chauds
Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes
AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.
Undress AI Tool
Images de déshabillage gratuites
Clothoff.io
Dissolvant de vêtements AI
AI Hentai Generator
Générez AI Hentai gratuitement.
Article chaud
Outils chauds
Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit
SublimeText3 version chinoise
Version chinoise, très simple à utiliser
Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP
Dreamweaver CS6
Outils de développement Web visuel
SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
Lisez des fichiers CSV et effectuez une analyse de données à l'aide de pandas
Jan 09, 2024 am 09:26 AM
Pandas est un puissant outil d'analyse de données qui peut facilement lire et traiter différents types de fichiers de données. Parmi eux, les fichiers CSV sont l’un des formats de fichiers de données les plus courants et les plus utilisés. Cet article expliquera comment utiliser Pandas pour lire des fichiers CSV et effectuer une analyse de données, et fournira des exemples de code spécifiques. 1. Importez les bibliothèques nécessaires Tout d'abord, nous devons importer la bibliothèque Pandas et les autres bibliothèques associées qui peuvent être nécessaires, comme indiqué ci-dessous : importpandasaspd 2. Lisez le fichier CSV à l'aide de Pan
Introduction aux méthodes d'analyse des données
Jan 08, 2024 am 10:22 AM
Méthodes courantes d'analyse des données : 1. Méthode d'analyse comparative ; 2. Méthode d'analyse structurelle ; 3. Méthode d'analyse croisée ; 5. Méthode d'analyse des causes et des effets ; , Méthode d'analyse en composantes principales ; 9. Méthode d'analyse de dispersion ; 10. Méthode d'analyse matricielle. Introduction détaillée : 1. Méthode d'analyse comparative : Analyse comparative de deux ou plusieurs données pour trouver les différences et les modèles ; 2. Méthode d'analyse structurelle : Une méthode d'analyse comparative entre chaque partie de l'ensemble et l'ensemble. , etc.
11 distributions de base que les data scientists utilisent 95 % du temps
Dec 15, 2023 am 08:21 AM
Suite au dernier inventaire des « 11 graphiques de base que les data scientists utilisent 95 % du temps », nous vous présenterons aujourd'hui 11 distributions de base que les data scientists utilisent 95 % du temps. La maîtrise de ces distributions nous aide à comprendre plus profondément la nature des données et à faire des inférences et des prédictions plus précises lors de l'analyse des données et de la prise de décision. 1. Distribution normale La distribution normale, également connue sous le nom de distribution gaussienne, est une distribution de probabilité continue. Il présente une courbe symétrique en forme de cloche avec la moyenne (μ) comme centre et l'écart type (σ) comme largeur. La distribution normale a une valeur d'application importante dans de nombreux domaines tels que les statistiques, la théorie des probabilités et l'ingénierie.
Apprentissage automatique et analyse de données à l'aide du langage Go
Nov 30, 2023 am 08:44 AM
Dans la société intelligente d’aujourd’hui, l’apprentissage automatique et l’analyse des données sont des outils indispensables qui peuvent aider les individus à mieux comprendre et utiliser de grandes quantités de données. Dans ces domaines, le langage Go est également devenu un langage de programmation qui a beaucoup retenu l'attention. Sa rapidité et son efficacité en font le choix de nombreux programmeurs. Cet article explique comment utiliser le langage Go pour l'apprentissage automatique et l'analyse de données. 1. L'écosystème du langage Go d'apprentissage automatique n'est pas aussi riche que Python et R. Cependant, à mesure que de plus en plus de personnes commencent à l'utiliser, certaines bibliothèques et frameworks d'apprentissage automatique
11 visualisations avancées pour l'analyse des données et l'apprentissage automatique
Oct 25, 2023 am 08:13 AM
La visualisation est un outil puissant pour communiquer des modèles et des relations de données complexes de manière intuitive et compréhensible. Ils jouent un rôle essentiel dans l’analyse des données, fournissant des informations souvent difficiles à discerner à partir de données brutes ou de représentations numériques traditionnelles. La visualisation est cruciale pour comprendre les modèles et les relations de données complexes, et nous présenterons les 11 graphiques les plus importants et incontournables qui aident à révéler les informations contenues dans les données et à rendre les données complexes plus compréhensibles et significatives. 1. KSPlotKSPlot est utilisé pour évaluer les différences de distribution. L'idée principale est de mesurer la distance maximale entre les fonctions de distribution cumulatives (CDF) de deux distributions. Plus la distance maximale est petite, plus ils appartiennent probablement à la même distribution. Par conséquent, il est principalement interprété comme un « système » permettant de déterminer les différences de distribution.
Comment utiliser les interfaces ECharts et PHP pour mettre en œuvre l'analyse des données et la prédiction de graphiques statistiques
Dec 17, 2023 am 10:26 AM
Comment utiliser les interfaces ECharts et PHP pour mettre en œuvre l'analyse des données et la prédiction des graphiques statistiques. L'analyse et la prédiction des données jouent un rôle important dans divers domaines. Elles peuvent nous aider à comprendre les tendances et les modèles de données et fournir des références pour les décisions futures. ECharts est une bibliothèque de visualisation de données open source qui fournit des composants graphiques riches et flexibles capables de charger et de traiter dynamiquement des données à l'aide de l'interface PHP. Cet article présentera la méthode de mise en œuvre de l'analyse et de la prédiction des données de graphiques statistiques basée sur ECharts et l'interface PHP, et fournira
Le voyage romantique de Python et de l'apprentissage automatique, un pas de novice à expert
Feb 23, 2024 pm 08:34 PM
1. La rencontre entre Python et l'apprentissage automatique En tant que langage de programmation facile à apprendre et puissant, Python est profondément apprécié des développeurs. L’apprentissage automatique, en tant que branche de l’intelligence artificielle, vise à permettre aux ordinateurs d’apprendre à tirer des leçons des données et de faire des prédictions ou des décisions. La combinaison de Python et de l'apprentissage automatique est une combinaison parfaite, nous apportant une série d'outils et de bibliothèques puissants, rendant l'apprentissage automatique plus facile à mettre en œuvre et à appliquer. 2. Explorer la bibliothèque d'apprentissage automatique de Python Python fournit de nombreuses bibliothèques d'apprentissage automatique riches en fonctionnalités, dont les plus populaires incluent : NumPy : fournit des fonctions de calcul numérique efficaces et constitue la bibliothèque de base pour l'apprentissage automatique. SciPy : fournit des outils de calcul scientifique plus avancés,
Quelles industries ont une plus grande demande pour le langage Go ?
Feb 21, 2024 pm 10:39 PM
Dans l'ère technologique actuelle en développement rapide, divers langages de programmation sont de plus en plus utilisés dans une gamme de plus en plus large d'applications. Parmi eux, le langage Go, en tant que langage de programmation efficace, concis, facile à apprendre et à utiliser, est favorisé par de plus en plus d'entreprises. et les développeurs. Le langage Go (également connu sous le nom de Golang) est un langage de programmation développé par Google. Il met l'accent sur la simplicité, l'efficacité et la programmation simultanée et convient à divers scénarios d'application. Alors, quelles industries ont une plus grande demande pour le langage Go ? Ensuite, nous analyserons certaines industries majeures et explorerons leurs besoins en langage Go. l'Internet
