 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Plus de 70 % de mAP pour la première fois ! GeMap : Carte locale de haute précision SOTA à nouveau actualisée
Plus de 70 % de mAP pour la première fois ! GeMap : Carte locale de haute précision SOTA à nouveau actualisée
Plus de 70 % de mAP pour la première fois ! GeMap : Carte locale de haute précision SOTA à nouveau actualisée
Écrit ci-dessus et compréhension personnelle de l'auteur
La construction de cartes vectorisées de haute précision basées sur les données de capteurs en temps réel est cruciale pour les tâches en aval telles que la prévision et la planification, et peut efficacement compenser les mauvaises performances en temps réel du mode hors ligne. cartes de haute précision. Avec le développement de l'apprentissage profond, la construction de cartes vectorielles en ligne de haute précision a progressivement émergé, et des ouvrages représentatifs tels que HDMapNet, MapTR, etc. ont vu le jour les uns après les autres. Cependant, les méthodes existantes de construction de cartes vectorielles en ligne de haute précision manquent d'exploration des propriétés géométriques des éléments cartographiques (y compris la forme des éléments, les relations verticales, parallèles et autres relations géométriques).
Propriétés géométriques des cartes vectorisées de haute précision
Les cartes vectorisées de haute précision résument fortement les éléments sur la route et représentent chaque élément de la carte sous la forme d'une séquence de points bidimensionnelle. La conception des routes urbaines a des spécifications spécifiques. Par exemple, dans la plupart des cas, les passages pour piétons sont carrés rectangulaires ou parallélogrammes ; Différents éléments des cartes haute définition présentent également de nombreuses caractéristiques similaires. Ces règles de bon sens sont résumées dans les propriétés géométriques des cartes haute précision, y compris la forme des éléments cartographiques (rectangle, parallélogramme, ligne droite, etc. ), ou différentes cartes Relations entre éléments (parallèles, verticales, etc.). Les propriétés géométriques limitent fortement la représentation des éléments cartographiques. Si vous comprenez parfaitement les propriétés géométriques de la construction de modèles en ligne, vous pouvez obtenir des résultats plus précis.
Proposer l'importance de la représentation géométrique pour les cartes de haute précisionBien qu'en théorie, il soit encore possible pour les modèles existants d'apprendre les propriétés géométriques des éléments cartographiques, les caractéristiques des propriétés géométriques déterminent que, du moins dans les conditions traditionnelles design, le modèle n'est pas facile à apprendre.
- Invariance des propriétés géométriques
- Lorsque le véhicule central roule tout droit sur la route, change de voie ou tourne, les
des éléments de la carte (dans le système de coordonnées du véhicule) continuent de changer. La forme des passages pour piétons, des voies, des limites des routes, etc. ne changera pas, de même que la relation parallèle entre les voies ne changera pas. Les propriétés géométriques des éléments cartographiques sont objectives et l'une de ses caractéristiques importantes est l'invariance. Plus précisément, il s'agit de invariance rigide (restant invariant à la transformation en rotation et en translation). Les travaux antérieurs, qu'ils utilisent une simple représentation polyligne ou des courbes polynomiales avec des points de contrôle (telles que les courbes de Bézier, les courbes de Bézier par morceaux), sont tous basés sur des coordonnées absolues et de bout en bout sur la base de l'optimisation des coordonnées absolues. L'objectif d'optimisation basé sur les coordonnées absolues lui-même n'a pas d'invariance rigide, il est donc difficile de s'attendre à ce que la solution optimale locale dans laquelle s'inscrit le modèle contienne une compréhension des propriétés géométriques. Par conséquent, une représentation capable de caractériser pleinement les propriétés géométriques et de présenter une certaine invariance est nécessaire.
Figure 1. Exemple d'invariance géométrique. Lorsque le véhicule tourne à droite, les coordonnées absolues changeront considérablement. L'image de droite montre un scénario réel correspondant.
Lorsque le véhicule tourne à droite, les coordonnées absolues changeront considérablement. L'image de droite montre un scénario réel correspondant.
- Diversité des propriétés géométriques
- De plus, malgré de solides connaissances préalables, les propriétés géométriques des routes sont encore diverses. Ces diverses propriétés géométriques peuvent généralement être divisées en deux catégories, l’une concerne la forme géométrique d’un seul élément cartographique et l’autre concerne l’association géométrique de différents éléments cartographiques. En raison de la diversité des propriétés géométriques, il est impossible de convertir manuellement et de manière exhaustive les propriétés géométriques en contraintes. Nous préférons donc que le modèle puisse apprendre de manière autonome une variété de propriétés géométriques de bout en bout.
Conception de GeMap
Représentation géométriqueCompte tenu des deux problèmes ci-dessus, nous améliorons d'abord la méthode de représentation. Nous espérons introduire une bonne représentation géométrique en plus de la représentation traditionnelle basée sur des coordonnées absolues, qui doit répondre aux exigences suivantes :
peut décrire la forme des éléments de la carte
peut décrire l'- association
- entre éléments cartographiques Rigidité invariance
- Pour assurer
- l'invariance de translation , nous utilisons une quantité relative, c'est-à-dire le vecteur de décalage entre les points pour garantir davantage l'invariance de rotation , nous choisissons la longueur du
, et l'angle entre différents vecteurs de décalage. Ces deux éléments - longueur et angle - constituent la base de la représentation géométrique que nous proposons. De plus, afin de mieux distinguer et décrire les formes et relier deux types différents de propriétés géométriques, nous avons affiné le design selon le principe de simplicité : Pour décrire des formes, nous calculons la distance entre des points adjacents dans un un seul élément de carte décale les vecteurs entre eux et calcule la longueur du vecteur de décalage et l'angle entre les vecteurs de décalage adjacents. Cette représentation identifie de manière unique toute polyligne/polygone. Des exemples de deux images sont présentés ci-dessous :
Veuillez regarder la figure 2, qui montre la représentation des formes géométriques
Pour un rectangle, il peut être décrit en utilisant un angle droit et deux paires de côtés égaux pour une ligne droite, tous les angles inclus sont de 0 degré ou 180 degrés ; .
Pour caractériser association, de la même manière, nous considérons d'abord la distance entre deux points quelconques. Cependant, si l’angle est calculé pour tous les vecteurs de décalage point à point, la complexité de la représentation est trop élevée et le coût de calcul est inabordable. Plus précisément, en supposant qu'il y a un total d'éléments cartographiques et que chaque élément est représenté par un point, la quantité de données pour tous les angles atteindra (en prenant 1 000, en supposant que chaque donnée d'angle est un nombre à virgule flottante de 32 bits, tel que une représentation est seulement L'espace occupé atteindra le niveau TB). En fait, cela n’est pas nécessaire pour les relations normales verticales, parallèles, etc. Par conséquent, nous calculons d’abord les décalages au sein des éléments, puis calculons uniquement l’angle entre chaque paire de ces décalages dans le cadre de la représentation géométrique. Cette représentation d'association simplifiée conserve la capacité de décrire des relations parallèles, verticales et autres, alors que le volume de données correspondant est seulement (environ 4 Mo dans les conditions susmentionnées). Pour faciliter la compréhension, nous fournissons également quelques exemples :
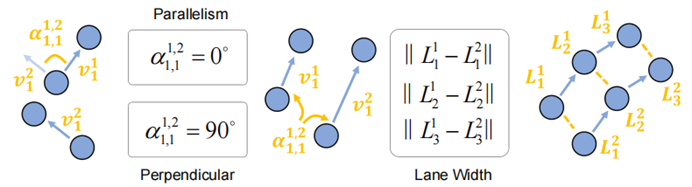
Figure 3. Représentation d'association géométrique.
La relation parallèle et la relation perpendiculaire sont exprimées par l'angle entre le vecteur de décalage étant de 0 degré ou 90 degrés ; la distance entre les deux points peut refléter dans une certaine mesure les informations sur la largeur de la voie
C'est la représentation de formes et associations géométriques optimisées, nous adoptons l'approche la plus simple, calculons directement la représentation géométrique de la prédiction et de l'étiquette, puis utilisons la norme comme cible d'optimisation :
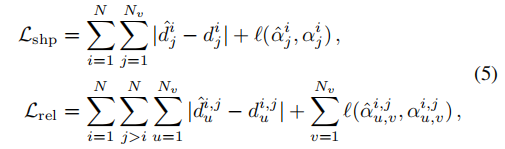
où et représentent la longueur et l'angle calculés en fonction de l'étiquette, respectivement, et la somme représentent la prévision de la longueur et de l'angle calculés. Une astuce est utilisée lorsqu'il s'agit d'angles inclus : le calcul direct de l'angle implique une fonction arctan discontinue, qui rencontrera des difficultés lors de l'optimisation (il y a un problème de gradient de disparition proche de ±90 degrés), donc ce que l'on compare en réalité, c'est l'angle inclus. Les cosinus et sinus de La robustesse de
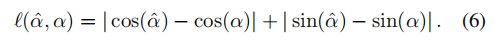 Attention géométriquement découplée
Attention géométriquement découplée
Dans l'auto-attention, toutes les requêtes (c'est-à-dire les « points ») interagissent de manière égale les unes avec les autres. Cependant, la forme de l’élément map correspond à un groupe de requêtes. L'interaction entre ces groupes devient un handicap lors de la perception de la forme des éléments. Au contraire, dans la perception de la relation entre les éléments, la forme est également devenue un facteur redondant. Cela signifie que
dissocier la perception de la forme et de l'association peut conduire à de meilleurs résultats.
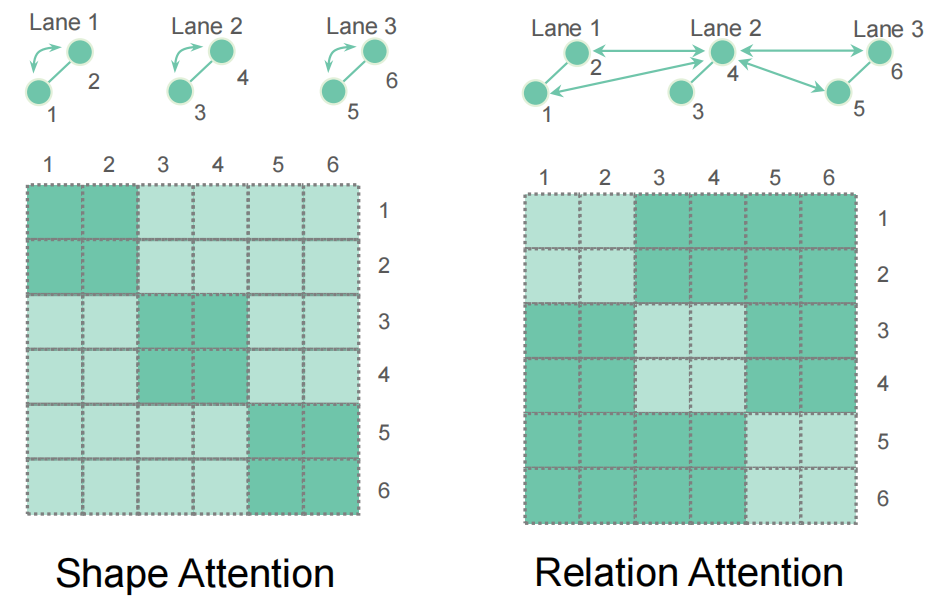
Afin de découpler la géométrie et le traitement d'association, nous utilisons deux étapes d'auto-attention : Chaque élément de la carte comprend
requêtes, et l'attention est effectuée à l'intérieur de ces requêtes pour le traitement des formes géométriques- complètent les relations d'attention à travers les éléments pour gérer les associations géométriques L'attention du découplage géométrique peut être représentée de manière plus vivante par la figure suivante. Notre implémentation est relativement simple, utilisant directement des masques pour contrôler la portée de l'attention. Puisque ces deux types d'attention sont complémentaires, avec une mise en œuvre raisonnable, la complexité temporelle peut être équivalente à la réalisation d'une seule auto-attention
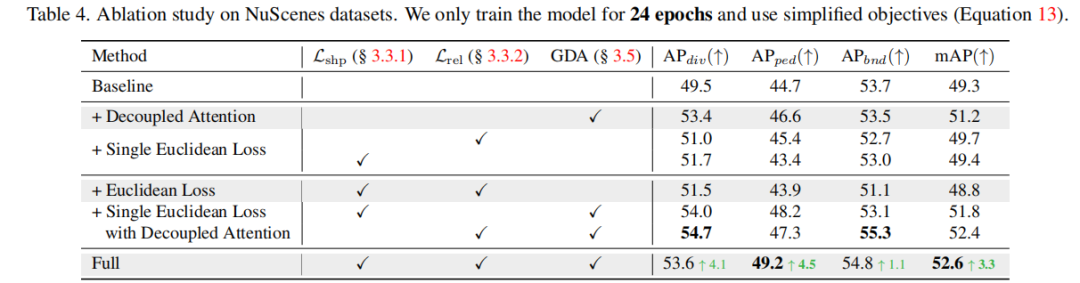
Nous avons mené un grand nombre d'expériences sur les ensembles de données nuScenes et Argoverse 2. Les deux sont des ensembles de données de conduite autonome à grande échelle couramment utilisés et fournissent tous deux des annotations cartographiques.
Principaux résultats
Nous avons mené trois séries d'expériences sur nuScenes. Premièrement, nous utilisons une combinaison relativement pure de fonctions objectives, incluant uniquement les pertes géométriques et d'autres pertes nécessaires (telles que la distance point à point, la direction des bords, la classification). Cette combinaison vise à mettre en évidence l'importance des propriétés géométriques que nous proposons. valeur sans trop rechercher les résultats SOTA. Les résultats montrent que notre méthode améliore mAP par rapport à MapTR dans ce cas. Pour explorer les limites de GeMap, nous ajoutons également quelques objectifs auxiliaires, notamment la segmentation et l'estimation de la profondeur. Dans ce cas, nous avons également obtenu des résultats SOTA (amélioration mAP). Il convient de noter que parvenir à une telle amélioration ne nécessite pas de sacrifier trop de vitesse d’inférence. Enfin, nous avons également essayé d'introduire des entrées modales LiDAR supplémentaires. Avec l'aide d'entrées modales supplémentaires, les performances de GeMap ont été encore améliorées
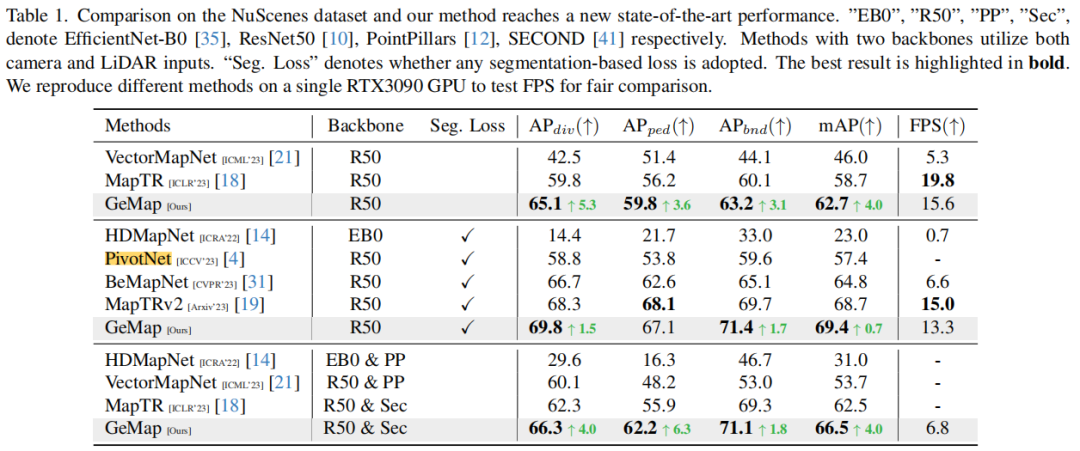
De même, sur l'ensemble de données Argoverse 2, notre méthode a également obtenu des résultats très remarquables.

Le contenu réécrit est : des expériences d'ablation
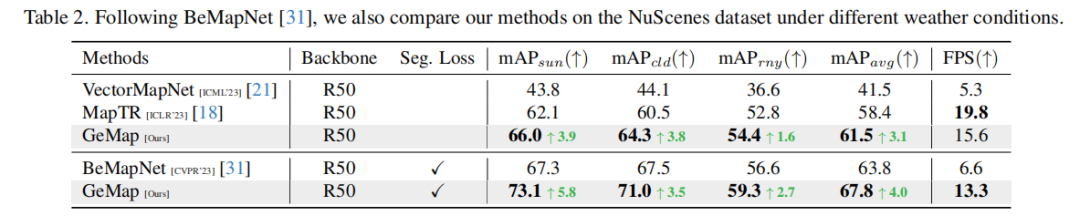
Le contenu réécrit supplémentaire sur nuScenes est : des expériences d'ablation prouvent la valeur de la perte géométrique et de l'attention géométriquement découplée. Fait intéressant, comme nous nous y attendions, l’utilisation directe de la perte géométrique entraînera une diminution des performances du modèle. Nous pensons que cela est dû au fait que le couplage structurel de la forme et du traitement d'association rend difficile pour le modèle l'optimisation de la représentation géométrique et après combinaison avec l'attention du découplage géométrique, la perte géométrique joue le rôle qui lui revient (de "+ Perte euclidienne" à "Complet").
Plus de résultats
De plus, nous avons également effectué une analyse visuelle de nuScenes. Les résultats de visualisation montrent que GeMap est non seulement robuste dans la gestion de la rotation et de la translation, mais présente également certains avantages dans la résolution des problèmes d'occlusion, comme le montre la figure ci-dessous. Les éléments cartographiques difficiles sont marqués par des cases orange dans la figure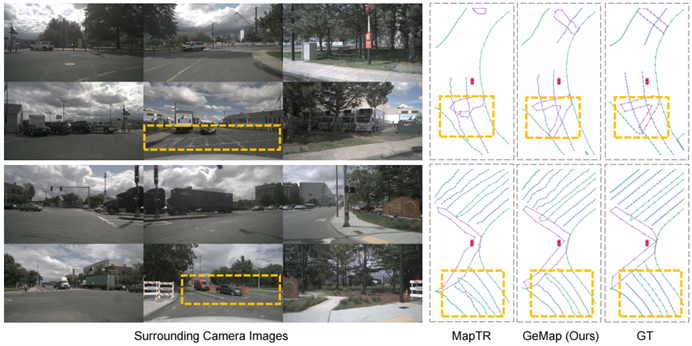
Résumé
Nous avons souligné les propriétés géométriques des éléments cartographiques et leur valeur pour la construction de cartes vectorisées en ligne de haute précision . Sur cette base, nous proposons une méthode puissante pour vérifier initialement cette valeur. De plus, la robustesse de GeMap à l'occlusion peut indiquer l'idée d'utiliser des propriétés géométriques pour gérer l'occlusion dans d'autres tâches de conduite autonome (telles que la détection, la prédiction d'occupation, etc.) - car les véhicules et les routes ont des propriétés géométriques relativement standardisées. Bien entendu, notre méthode elle-même a beaucoup à explorer davantage. Par exemple, des éléments géométriques de complexité différente peuvent-ils être décrits de manière adaptative en utilisant différents points ? Est-il possible de comprendre la représentation géométrique d’un point de vue probabiliste et de la rendre plus robuste au bruit ? Parce que nous avons simplifié l’association d’éléments, existe-t-il une meilleure représentation de l’association géométrique ? Ce sont toutes des directions pour une optimisation ultérieure.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment faire de Google Maps la carte par défaut sur iPhone
Apr 17, 2024 pm 07:34 PM
Comment faire de Google Maps la carte par défaut sur iPhone
Apr 17, 2024 pm 07:34 PM
La carte par défaut sur l'iPhone est Maps, le fournisseur de géolocalisation propriétaire d'Apple. Même si la carte s’améliore, elle ne fonctionne pas bien en dehors des États-Unis. Il n'a rien à offrir par rapport à Google Maps. Dans cet article, nous discutons des étapes réalisables pour utiliser Google Maps afin de devenir la carte par défaut sur votre iPhone. Comment faire de Google Maps la carte par défaut sur iPhone Définir Google Maps comme application cartographique par défaut sur votre téléphone est plus facile que vous ne le pensez. Suivez les étapes ci-dessous – Étapes préalables – Vous devez avoir Gmail installé sur votre téléphone. Étape 1 – Ouvrez l'AppStore. Étape 2 – Recherchez « Gmail ». Étape 3 – Cliquez à côté de l'application Gmail
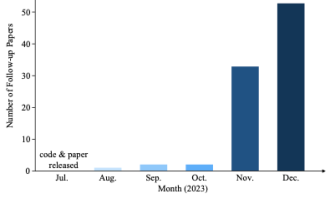 Pourquoi le Gaussian Splatting est-il si populaire dans la conduite autonome que le NeRF commence à être abandonné ?
Jan 17, 2024 pm 02:57 PM
Pourquoi le Gaussian Splatting est-il si populaire dans la conduite autonome que le NeRF commence à être abandonné ?
Jan 17, 2024 pm 02:57 PM
Écrit ci-dessus et compréhension personnelle de l'auteur Le Gaussiansplatting tridimensionnel (3DGS) est une technologie transformatrice qui a émergé dans les domaines des champs de rayonnement explicites et de l'infographie ces dernières années. Cette méthode innovante se caractérise par l’utilisation de millions de gaussiennes 3D, ce qui est très différent de la méthode du champ de rayonnement neuronal (NeRF), qui utilise principalement un modèle implicite basé sur les coordonnées pour mapper les coordonnées spatiales aux valeurs des pixels. Avec sa représentation explicite de scènes et ses algorithmes de rendu différenciables, 3DGS garantit non seulement des capacités de rendu en temps réel, mais introduit également un niveau de contrôle et d'édition de scène sans précédent. Cela positionne 3DGS comme un révolutionnaire potentiel pour la reconstruction et la représentation 3D de nouvelle génération. À cette fin, nous fournissons pour la première fois un aperçu systématique des derniers développements et préoccupations dans le domaine du 3DGS.
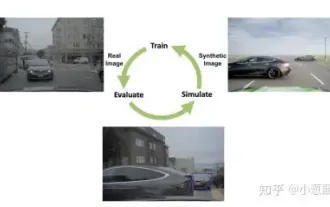 Comment résoudre le problème de la longue traîne dans les scénarios de conduite autonome ?
Jun 02, 2024 pm 02:44 PM
Comment résoudre le problème de la longue traîne dans les scénarios de conduite autonome ?
Jun 02, 2024 pm 02:44 PM
Hier, lors de l'entretien, on m'a demandé si j'avais posé des questions à longue traîne, j'ai donc pensé faire un bref résumé. Le problème à longue traîne de la conduite autonome fait référence aux cas extrêmes dans les véhicules autonomes, c'est-à-dire à des scénarios possibles avec une faible probabilité d'occurrence. Le problème perçu de la longue traîne est l’une des principales raisons limitant actuellement le domaine de conception opérationnelle des véhicules autonomes intelligents à véhicule unique. L'architecture sous-jacente et la plupart des problèmes techniques de la conduite autonome ont été résolus, et les 5 % restants des problèmes à longue traîne sont progressivement devenus la clé pour restreindre le développement de la conduite autonome. Ces problèmes incluent une variété de scénarios fragmentés, de situations extrêmes et de comportements humains imprévisibles. La « longue traîne » des scénarios limites dans la conduite autonome fait référence aux cas limites dans les véhicules autonomes (VA). Les cas limites sont des scénarios possibles avec une faible probabilité d'occurrence. ces événements rares
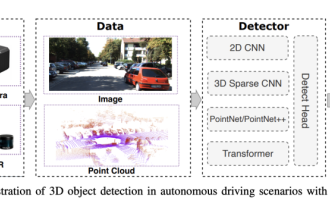 Choisir une caméra ou un lidar ? Une étude récente sur la détection robuste d'objets 3D
Jan 26, 2024 am 11:18 AM
Choisir une caméra ou un lidar ? Une étude récente sur la détection robuste d'objets 3D
Jan 26, 2024 am 11:18 AM
0. Écrit à l'avant&& Compréhension personnelle que les systèmes de conduite autonome s'appuient sur des technologies avancées de perception, de prise de décision et de contrôle, en utilisant divers capteurs (tels que caméras, lidar, radar, etc.) pour percevoir l'environnement et en utilisant des algorithmes et des modèles pour une analyse et une prise de décision en temps réel. Cela permet aux véhicules de reconnaître les panneaux de signalisation, de détecter et de suivre d'autres véhicules, de prédire le comportement des piétons, etc., permettant ainsi de fonctionner en toute sécurité et de s'adapter à des environnements de circulation complexes. Cette technologie attire actuellement une grande attention et est considérée comme un domaine de développement important pour l'avenir des transports. . un. Mais ce qui rend la conduite autonome difficile, c'est de trouver comment faire comprendre à la voiture ce qui se passe autour d'elle. Cela nécessite que l'algorithme de détection d'objets tridimensionnels du système de conduite autonome puisse percevoir et décrire avec précision les objets dans l'environnement, y compris leur emplacement,
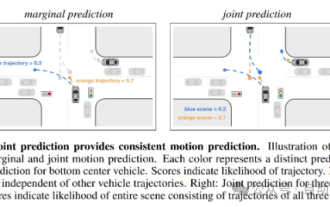 Cet article vous suffit pour en savoir plus sur la conduite autonome et la prédiction de trajectoire !
Feb 28, 2024 pm 07:20 PM
Cet article vous suffit pour en savoir plus sur la conduite autonome et la prédiction de trajectoire !
Feb 28, 2024 pm 07:20 PM
La prédiction de trajectoire joue un rôle important dans la conduite autonome. La prédiction de trajectoire de conduite autonome fait référence à la prédiction de la trajectoire de conduite future du véhicule en analysant diverses données pendant le processus de conduite du véhicule. En tant que module central de la conduite autonome, la qualité de la prédiction de trajectoire est cruciale pour le contrôle de la planification en aval. La tâche de prédiction de trajectoire dispose d'une riche pile technologique et nécessite une connaissance de la perception dynamique/statique de la conduite autonome, des cartes de haute précision, des lignes de voie, des compétences en architecture de réseau neuronal (CNN&GNN&Transformer), etc. Il est très difficile de démarrer ! De nombreux fans espèrent se lancer dans la prédiction de trajectoire le plus tôt possible et éviter les pièges. Aujourd'hui, je vais faire le point sur quelques problèmes courants et des méthodes d'apprentissage introductives pour la prédiction de trajectoire ! Connaissances introductives 1. Existe-t-il un ordre d'entrée pour les épreuves de prévisualisation ? R : Regardez d’abord l’enquête, p
 SIMPL : un benchmark de prédiction de mouvement multi-agents simple et efficace pour la conduite autonome
Feb 20, 2024 am 11:48 AM
SIMPL : un benchmark de prédiction de mouvement multi-agents simple et efficace pour la conduite autonome
Feb 20, 2024 am 11:48 AM
Titre original : SIMPL : ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Lien article : https://arxiv.org/pdf/2402.02519.pdf Lien code : https://github.com/HKUST-Aerial-Robotics/SIMPL Affiliation de l'auteur : Université des sciences de Hong Kong et technologie Idée DJI Paper : cet article propose une base de référence de prédiction de mouvement (SIMPL) simple et efficace pour les véhicules autonomes. Par rapport au cent agent traditionnel
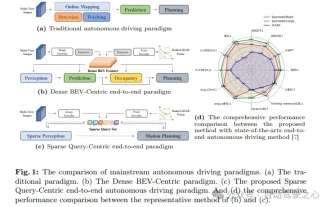 NuScenes dernier SOTA SparseAD : les requêtes clairsemées contribuent à une conduite autonome efficace de bout en bout !
Apr 17, 2024 pm 06:22 PM
NuScenes dernier SOTA SparseAD : les requêtes clairsemées contribuent à une conduite autonome efficace de bout en bout !
Apr 17, 2024 pm 06:22 PM
Écrit à l'avant et point de départ Le paradigme de bout en bout utilise un cadre unifié pour réaliser plusieurs tâches dans les systèmes de conduite autonome. Malgré la simplicité et la clarté de ce paradigme, les performances des méthodes de conduite autonome de bout en bout sur les sous-tâches sont encore loin derrière les méthodes à tâche unique. Dans le même temps, les fonctionnalités de vue à vol d'oiseau (BEV) denses, largement utilisées dans les méthodes de bout en bout précédentes, rendent difficile l'adaptation à davantage de modalités ou de tâches. Un paradigme de conduite autonome de bout en bout (SparseAD) centré sur la recherche clairsemée est proposé ici, dans lequel la recherche clairsemée représente entièrement l'ensemble du scénario de conduite, y compris l'espace, le temps et les tâches, sans aucune représentation BEV dense. Plus précisément, une architecture clairsemée unifiée est conçue pour la connaissance des tâches, notamment la détection, le suivi et la cartographie en ligne. De plus, lourd
 Parlons des systèmes de conduite autonome de bout en bout et de nouvelle génération, ainsi que de quelques malentendus sur la conduite autonome de bout en bout ?
Apr 15, 2024 pm 04:13 PM
Parlons des systèmes de conduite autonome de bout en bout et de nouvelle génération, ainsi que de quelques malentendus sur la conduite autonome de bout en bout ?
Apr 15, 2024 pm 04:13 PM
Au cours du mois dernier, pour des raisons bien connues, j'ai eu des échanges très intensifs avec divers professeurs et camarades de classe du secteur. Un sujet inévitable dans l'échange est naturellement le populaire Tesla FSDV12 de bout en bout. Je voudrais profiter de cette occasion pour trier certaines de mes pensées et opinions en ce moment pour votre référence et votre discussion. Comment définir un système de conduite autonome de bout en bout et quels problèmes devraient être résolus de bout en bout ? Selon la définition la plus traditionnelle, un système de bout en bout fait référence à un système qui saisit les informations brutes des capteurs et génère directement les variables pertinentes pour la tâche. Par exemple, en reconnaissance d'images, CNN peut être appelé de bout en bout par rapport à la méthode traditionnelle d'extraction de caractéristiques + classificateur. Dans les tâches de conduite autonome, saisir les données de divers capteurs (caméra/LiDAR





