 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Discuter de l'analyse de la planification d'itinéraire de l'algorithme de recherche de chemin et de la mise en œuvre du code
Discuter de l'analyse de la planification d'itinéraire de l'algorithme de recherche de chemin et de la mise en œuvre du code
Discuter de l'analyse de la planification d'itinéraire de l'algorithme de recherche de chemin et de la mise en œuvre du code

L'algorithme de recherche de chemin est l'un des algorithmes couramment utilisés dans le domaine de l'infographie et de l'intelligence artificielle, utilisé pour calculer le chemin le plus court ou le chemin optimal d'un point à un autre. Dans cet article, je présenterai en détail deux algorithmes de recherche de chemin couramment utilisés : l'algorithme de Dijkstra et l'algorithme A*
L'algorithme de Dijkstra
L'algorithme de Dijkstra est une méthode de largeur utilisée pour trouver le chemin le plus court entre deux points dans un graphe. algorithme de recherche. Cela fonctionne comme suit :
Nous devons créer un ensemble S pour stocker les sommets qui ont trouvé le chemin le plus court
Nous devons créer un ensemble Q pour stocker les sommets qui n'ont pas encore trouvé le chemin le plus court
Lors de l'initialisation Lorsque vous utilisez le tableau de distance dist, vous devez définir la distance du point de départ aux autres points à l'infini et la distance du point de départ à lui-même à 0
Répétez les étapes suivantes jusqu'à ce que l'ensemble soit défini. Q est vide :
- in Trouvez le sommet u le plus proche du point de départ dans l'ensemble Q et ajoutez-le à l'ensemble S.
- Pour chaque sommet voisin v du sommet u, mettez à jour la distance dist[v] du point de départ à v. Si dist[v] > dist[u] + edge(u, v), mettez à jour dist[v] est dist[u] + bord(u, v).
Enfin, le tableau dist stocke le chemin le plus court du point de départ à chaque sommet
Ce qui suit est le code source de l'algorithme de Dijkstra écrit en C# :
class DijkstraAlgorithm
{
private int[,] graph;
private int size;
public DijkstraAlgorithm(int[,] graph)
{
this.graph = graph;
this.size = graph.GetLength(0);
}
public int[] FindShortestPath(int start, int end)
{
int[] dist = new int[size];
bool[] visited = new bool[size];
for (int i = 0; i <h4 id="span-Un-algorithme-span"><span>Un algorithme</span></h4><p><span>A L'algorithme est un algorithme de recherche heuristique utilisé pour trouver le chemin le plus court entre deux points d'un graphique. L'idée de l'algorithme est la suivante : </span></p><p><span>Créer une file d'attente prioritaire openSet pour stocker les sommets à explorer</span></p><p><span>Nous devons créer un tableau nommé gScore pour stocker le coût réel du point de départ à chacun vertex</span></p><p> <span>Nous devons créer un tableau nommé fScore pour stocker le coût estimé du point de départ au point cible</span></p><p><span>Ajoutez le point de départ à openSet, définissez gScore[start] sur 0 et définissez fScore[start ] à 0 Coût estimé du point de départ au point cible </span></p><p><span> Répétez les étapes suivantes jusqu'à ce que openSet soit vide : </span></p>- Trouvez le sommet actuel avec le plus petit fScore dans openSet.
- Si le courant est égal au point cible, cela signifie que le chemin le plus court a été trouvé et le chemin est renvoyé.
- Supprimez le courant d'openSet.
- Pour chaque sommet voisin du courant, calculez le coût réel tempGScore du point de départ au voisin. Si tempGScore est inférieur à gScore[neighbor], mettez à jour gScore[neighbor] en tempGScore et calculez fScore[neighbor] =. gScore[voisin] + coût estimé. Si le voisin n'est pas dans openSet, ajoutez-le à openSet.
Si openSet est vide, cela signifie que le point cible ne peut pas être atteint et qu'une valeur nulle est renvoyée
Voici le code source de l'algorithme A* écrit en Java :
import java.util.*;class AStarAlgorithm {private int[][] graph;private int size;public AStarAlgorithm(int[][] graph) {this.graph = graph;this.size = graph.length;}public List<integer> findShortestPath(int start, int end) {PriorityQueue<node> openSet = new PriorityQueue();int[] gScore = new int[size];int[] fScore = new int[size];int[] cameFrom = new int[size];boolean[] visited = new boolean[size];Arrays.fill(gScore, Integer.MAX_VALUE);Arrays.fill(fScore, Integer.MAX_VALUE);Arrays.fill(cameFrom, -1);gScore[start] = 0;fScore[start] = heuristicCostEstimate(start, end);openSet.offer(new Node(start, fScore[start]));while (!openSet.isEmpty()) {int current = openSet.poll().index;if (current == end) {return reconstructPath(cameFrom, current);}visited[current] = true;for (int neighbor = 0; neighbor reconstructPath(int[] cameFrom, int current) {List<integer> path = new ArrayList();path.add(current);while (cameFrom[current] != -1) {current = cameFrom[current];path.add(0, current);}return path;}private class Node implements Comparable<node> {public int index;public int fScore;public Node(int index, int fScore) {this.index = index;this.fScore = fScore;}@Overridepublic int compareTo(Node other) {return Integer.compare(this.fScore, other.fScore);}@Overridepublic boolean equals(Object obj) {if (this == obj) {return true;}if (obj == null || getClass() != obj.getClass()) {return false;}Node other = (Node) obj;return index == other.index;}@Overridepublic int hashCode() {return Objects.hash(index);}}}</node></integer></node></integer> Ce qui précède est une comparaison de l'algorithme de Dijkstra et d'A* Introduction détaillée de l'algorithme, y compris les idées d'algorithme, les processus et le code source implémentés en C# ou Java. Ces deux algorithmes sont des algorithmes de recherche de chemin couramment utilisés et peuvent être sélectionnés et utilisés en fonction de besoins spécifiques.
Bien sûr, dans les villes d’aujourd’hui, les logiciels de navigation peuvent planifier les choses pour nous.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Top 5 Genai Lunets de février 2025: GPT-4.5, Grok-3 et plus!
Mar 22, 2025 am 10:58 AM
Top 5 Genai Lunets de février 2025: GPT-4.5, Grok-3 et plus!
Mar 22, 2025 am 10:58 AM
Février 2025 a été un autre mois qui change la donne pour une IA générative, nous apportant certaines des mises à niveau des modèles les plus attendues et de nouvelles fonctionnalités révolutionnaires. De Xai's Grok 3 et Anthropic's Claude 3.7 Sonnet, à Openai's G
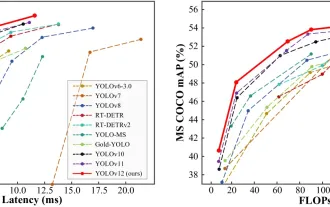 Comment utiliser YOLO V12 pour la détection d'objets?
Mar 22, 2025 am 11:07 AM
Comment utiliser YOLO V12 pour la détection d'objets?
Mar 22, 2025 am 11:07 AM
Yolo (vous ne regardez qu'une seule fois) a été un cadre de détection d'objets en temps réel de premier plan, chaque itération améliorant les versions précédentes. La dernière version Yolo V12 introduit des progrès qui améliorent considérablement la précision
 Meilleurs générateurs d'art AI (gratuit & amp; payé) pour des projets créatifs
Apr 02, 2025 pm 06:10 PM
Meilleurs générateurs d'art AI (gratuit & amp; payé) pour des projets créatifs
Apr 02, 2025 pm 06:10 PM
L'article passe en revue les meilleurs générateurs d'art AI, discutant de leurs fonctionnalités, de leur aptitude aux projets créatifs et de la valeur. Il met en évidence MidJourney comme la meilleure valeur pour les professionnels et recommande Dall-E 2 pour un art personnalisable de haute qualité.
 Chatgpt 4 o est-il disponible?
Mar 28, 2025 pm 05:29 PM
Chatgpt 4 o est-il disponible?
Mar 28, 2025 pm 05:29 PM
Chatgpt 4 est actuellement disponible et largement utilisé, démontrant des améliorations significatives dans la compréhension du contexte et la génération de réponses cohérentes par rapport à ses prédécesseurs comme Chatgpt 3.5. Les développements futurs peuvent inclure un interg plus personnalisé
 Meilleurs chatbots AI comparés (Chatgpt, Gemini, Claude & amp; plus)
Apr 02, 2025 pm 06:09 PM
Meilleurs chatbots AI comparés (Chatgpt, Gemini, Claude & amp; plus)
Apr 02, 2025 pm 06:09 PM
L'article compare les meilleurs chatbots d'IA comme Chatgpt, Gemini et Claude, en se concentrant sur leurs fonctionnalités uniques, leurs options de personnalisation et leurs performances dans le traitement et la fiabilité du langage naturel.
 Début avec Meta Llama 3.2 - Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
Début avec Meta Llama 3.2 - Analytics Vidhya
Apr 11, 2025 pm 12:04 PM
META'S LLAMA 3.2: un bond en avant dans l'IA multimodal et mobile Meta a récemment dévoilé Llama 3.2, une progression importante de l'IA avec de puissantes capacités de vision et des modèles de texte légers optimisés pour les appareils mobiles. S'appuyer sur le succès o
 Assistants d'écriture de l'IA pour augmenter votre création de contenu
Apr 02, 2025 pm 06:11 PM
Assistants d'écriture de l'IA pour augmenter votre création de contenu
Apr 02, 2025 pm 06:11 PM
L'article traite des meilleurs assistants d'écriture d'IA comme Grammarly, Jasper, Copy.ai, WireSonic et Rytr, en se concentrant sur leurs fonctionnalités uniques pour la création de contenu. Il soutient que Jasper excelle dans l'optimisation du référencement, tandis que les outils d'IA aident à maintenir le ton
 Comment utiliser Mistral OCR pour votre prochain modèle de chiffon
Mar 21, 2025 am 11:11 AM
Comment utiliser Mistral OCR pour votre prochain modèle de chiffon
Mar 21, 2025 am 11:11 AM
Mistral OCR: révolutionner la génération de la récupération avec une compréhension du document multimodal Les systèmes de génération (RAG) (RAG) de la récupération ont considérablement avancé les capacités d'IA, permettant à de vastes magasins de données pour une responsabilité plus éclairée





