 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Améliorez les points clés de Pytorch et améliorez l'optimiseur !
Améliorez les points clés de Pytorch et améliorez l'optimiseur !
Améliorez les points clés de Pytorch et améliorez l'optimiseur !
Salut, je m'appelle Xiaozhuang !
Aujourd'hui, nous parlons de l'optimiseur dans Pytorch.
Le choix de l'optimiseur a un impact direct sur l'effet d'entraînement et la rapidité du modèle d'apprentissage profond. Différents optimiseurs sont adaptés à différents problèmes, et leurs différences de performances peuvent amener le modèle à converger plus rapidement et de manière plus stable, ou à mieux fonctionner sur une tâche spécifique. Par conséquent, lors du choix d’un optimiseur, des compromis et des décisions doivent être faits en fonction des caractéristiques du problème spécifique.
Par conséquent, choisir le bon optimiseur est crucial pour régler les modèles d’apprentissage profond. Le choix de l'optimiseur affectera non seulement de manière significative les performances du modèle, mais également l'efficacité du processus de formation.
PyTorch fournit une variété d'optimiseurs qui peuvent être utilisés pour entraîner les réseaux de neurones et mettre à jour les poids des modèles. Ces optimiseurs incluent les communs SGD, Adam, RMSprop, etc. Chaque optimiseur a ses caractéristiques uniques et ses scénarios applicables. Le choix d'un optimiseur approprié peut accélérer la convergence des modèles et améliorer les résultats de la formation. Lorsque vous utilisez l'optimiseur, vous devez définir des hyperparamètres tels que le taux d'apprentissage et la perte de poids, ainsi que définir des fonctions de perte et des paramètres de modèle.

Optimiseurs courants
Listons d'abord quelques optimiseurs couramment utilisés dans PyTorch et donnons-en une brève introduction :
Comprenons comment fonctionne SGD (descente de gradient stochastique). SGD est un algorithme d'optimisation couramment utilisé pour résoudre les paramètres des modèles d'apprentissage automatique. Il estime le gradient en sélectionnant aléatoirement un petit lot d’échantillons et utilise la direction négative du gradient pour mettre à jour les paramètres. Cela permet d'optimiser progressivement les performances du modèle au cours d'un processus itératif. L'avantage de SGD est une efficacité de calcul élevée, particulièrement adaptée à la
La descente de gradient stochastique est un algorithme d'optimisation couramment utilisé pour minimiser la fonction de perte. Il fonctionne en calculant le gradient des poids par rapport à la fonction de perte et en mettant à jour les poids dans le sens négatif du gradient. Cet algorithme est largement utilisé en apprentissage automatique et en apprentissage profond.
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
(2) Adam
Adam est un algorithme d'optimisation du taux d'apprentissage adaptatif qui combine les idées d'AdaGrad et de RMSProp. Par rapport à l'algorithme traditionnel de descente de gradient, Adam peut calculer différents taux d'apprentissage pour chaque paramètre, s'adaptant ainsi mieux aux caractéristiques des différents paramètres. En ajustant de manière adaptative le taux d'apprentissage, Adam peut améliorer la vitesse de convergence et les performances du modèle.
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
(3) Adagrad
Adagrad est un algorithme d'optimisation du taux d'apprentissage adaptatif qui ajuste le taux d'apprentissage en fonction du gradient historique des paramètres. Cependant, à mesure que le taux d’apprentissage diminue progressivement, la formation peut s’arrêter prématurément.
optimizer = torch.optim.Adagrad(model.parameters(), lr=learning_rate)
(4) RMSProp
RMSProp est également un algorithme de taux d'apprentissage adaptatif qui ajuste le taux d'apprentissage en considérant la moyenne mobile du gradient.
optimizer = torch.optim.RMSprop(model.parameters(), lr=learning_rate)
(5) Adadelta
Adadelta est un algorithme d'optimisation du taux d'apprentissage adaptatif et une version améliorée de RMSProp, qui ajuste dynamiquement le taux d'apprentissage en considérant la moyenne mobile du gradient et la moyenne mobile des paramètres.
optimizer = torch.optim.Adadelta(model.parameters(), lr=learning_rate)
Un cas complet
Ici, parlons de la façon d'utiliser PyTorch pour former un simple réseau neuronal convolutionnel (CNN) pour la reconnaissance de chiffres manuscrits.
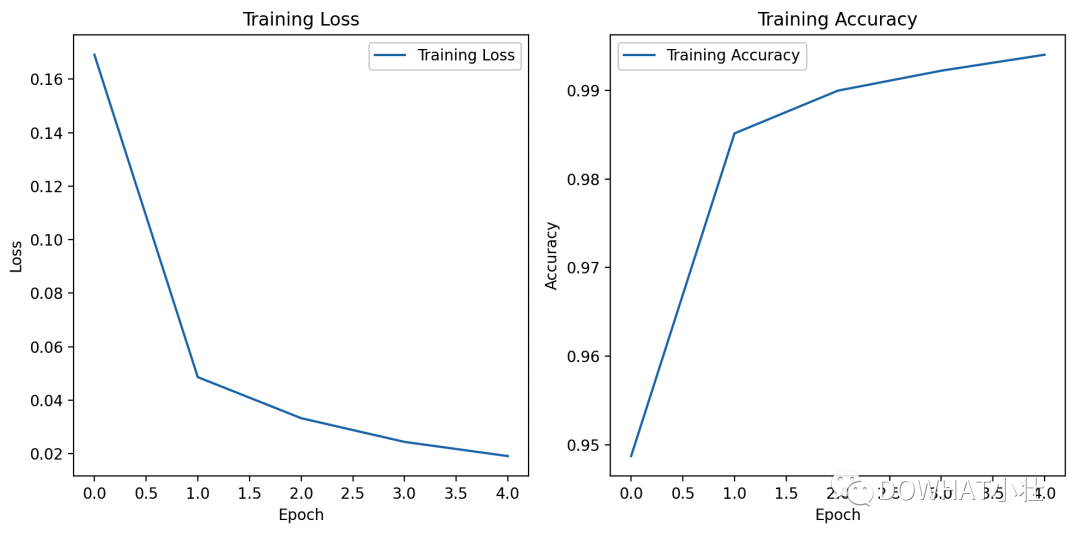
Ce cas utilise l'ensemble de données MNIST et utilise la bibliothèque Matplotlib pour tracer la courbe de perte et la courbe de précision.
import torchimport torch.nn as nnimport torch.optim as optimfrom torchvision import datasets, transformsfrom torch.utils.data import DataLoaderimport matplotlib.pyplot as plt# 设置随机种子torch.manual_seed(42)# 定义数据转换transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))])# 下载和加载MNIST数据集train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)test_loader = DataLoader(test_dataset, batch_size=1000, shuffle=False)# 定义简单的卷积神经网络模型class CNN(nn.Module):def __init__(self):super(CNN, self).__init__()self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1)self.relu = nn.ReLU()self.pool = nn.MaxPool2d(kernel_size=2, stride=2)self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)self.fc1 = nn.Linear(64 * 7 * 7, 128)self.fc2 = nn.Linear(128, 10)def forward(self, x):x = self.conv1(x)x = self.relu(x)x = self.pool(x)x = self.conv2(x)x = self.relu(x)x = self.pool(x)x = x.view(-1, 64 * 7 * 7)x = self.fc1(x)x = self.relu(x)x = self.fc2(x)return x# 创建模型、损失函数和优化器model = CNN()criterion = nn.CrossEntropyLoss()optimizer = optim.Adam(model.parameters(), lr=0.001)# 训练模型num_epochs = 5train_losses = []train_accuracies = []for epoch in range(num_epochs):model.train()total_loss = 0.0correct = 0total = 0for inputs, labels in train_loader:optimizer.zero_grad()outputs = model(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()total_loss += loss.item()_, predicted = torch.max(outputs.data, 1)total += labels.size(0)correct += (predicted == labels).sum().item()accuracy = correct / totaltrain_losses.append(total_loss / len(train_loader))train_accuracies.append(accuracy)print(f"Epoch {epoch+1}/{num_epochs}, Loss: {train_losses[-1]:.4f}, Accuracy: {accuracy:.4f}")# 绘制损失曲线和准确率曲线plt.figure(figsize=(10, 5))plt.subplot(1, 2, 1)plt.plot(train_losses, label='Training Loss')plt.title('Training Loss')plt.xlabel('Epoch')plt.ylabel('Loss')plt.legend()plt.subplot(1, 2, 2)plt.plot(train_accuracies, label='Training Accuracy')plt.title('Training Accuracy')plt.xlabel('Epoch')plt.ylabel('Accuracy')plt.legend()plt.tight_layout()plt.show()# 在测试集上评估模型model.eval()correct = 0total = 0with torch.no_grad():for inputs, labels in test_loader:outputs = model(inputs)_, predicted = torch.max(outputs.data, 1)total += labels.size(0)correct += (predicted == labels).sum().item()accuracy = correct / totalprint(f"Accuracy on test set: {accuracy * 100:.2f}%")Dans le code ci-dessus, nous définissons un simple réseau de neurones convolutifs (CNN), entraîné à l'aide de la perte d'entropie croisée et de l'optimiseur Adam.
Pendant le processus de formation, nous avons enregistré la perte et la précision de chaque époque, et utilisé la bibliothèque Matplotlib pour tracer la courbe de perte et la courbe de précision.
Je m'appelle Xiao Zhuang, à la prochaine fois !
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 iFlytek : les capacités de l'Ascend 910B de Huawei sont fondamentalement comparables à celles de l'A100 de Nvidia, et ils travaillent ensemble pour créer une nouvelle base pour l'intelligence artificielle générale de mon pays
Oct 22, 2023 pm 06:13 PM
iFlytek : les capacités de l'Ascend 910B de Huawei sont fondamentalement comparables à celles de l'A100 de Nvidia, et ils travaillent ensemble pour créer une nouvelle base pour l'intelligence artificielle générale de mon pays
Oct 22, 2023 pm 06:13 PM
Ce site a rapporté le 22 octobre qu'au troisième trimestre de cette année, iFlytek a réalisé un bénéfice net de 25,79 millions de yuans, soit une baisse de 81,86 % sur un an ; diminution d'une année sur l'autre de 76,36%. Jiang Tao, vice-président d'iFlytek, a révélé lors de la séance d'information sur les performances du troisième trimestre qu'iFlytek avait lancé un projet de recherche spécial avec Huawei Shengteng début 2023 et développé conjointement une bibliothèque d'opérateurs hautes performances avec Huawei pour créer conjointement une nouvelle base pour l'artificiel général de la Chine. intelligence pour permettre des modèles nationaux à grande échelle L'architecture est basée sur des logiciels et du matériel innovants indépendamment. Il a souligné que les capacités actuelles de l’Ascend 910B de Huawei sont fondamentalement comparables à celles de l’A100 de Nvidia. Lors du prochain iFlytek 1024 Global Developer Festival, iFlytek et Huawei feront d'autres annonces conjointes sur la base de puissance de calcul de l'intelligence artificielle. Il a également mentionné,
 La combinaison parfaite de PyCharm et PyTorch : étapes détaillées d'installation et de configuration
Feb 21, 2024 pm 12:00 PM
La combinaison parfaite de PyCharm et PyTorch : étapes détaillées d'installation et de configuration
Feb 21, 2024 pm 12:00 PM
PyCharm est un puissant environnement de développement intégré (IDE) et PyTorch est un framework open source populaire dans le domaine de l'apprentissage profond. Dans le domaine de l'apprentissage automatique et de l'apprentissage profond, l'utilisation de PyCharm et PyTorch pour le développement peut améliorer considérablement l'efficacité du développement et la qualité du code. Cet article présentera en détail comment installer et configurer PyTorch dans PyCharm, et joindra des exemples de code spécifiques pour aider les lecteurs à mieux utiliser les puissantes fonctions de ces deux éléments. Étape 1 : Installer PyCharm et Python
 Introduction à cinq méthodes d'échantillonnage dans les tâches de génération de langage naturel et l'implémentation du code Pytorch
Feb 20, 2024 am 08:50 AM
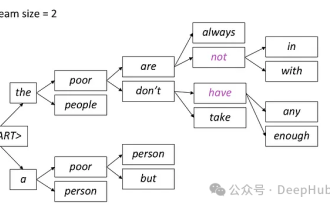
Introduction à cinq méthodes d'échantillonnage dans les tâches de génération de langage naturel et l'implémentation du code Pytorch
Feb 20, 2024 am 08:50 AM
Dans les tâches de génération de langage naturel, la méthode d'échantillonnage est une technique permettant d'obtenir du texte à partir d'un modèle génératif. Cet article abordera 5 méthodes courantes et les implémentera à l'aide de PyTorch. 1. GreedyDecoding Dans le décodage gourmand, le modèle génératif prédit les mots de la séquence de sortie en fonction du temps de la séquence d'entrée pas à pas. À chaque pas de temps, le modèle calcule la distribution de probabilité conditionnelle de chaque mot, puis sélectionne le mot avec la probabilité conditionnelle la plus élevée comme sortie du pas de temps actuel. Ce mot devient l'entrée du pas de temps suivant et le processus de génération se poursuit jusqu'à ce qu'une condition de fin soit remplie, telle qu'une séquence d'une longueur spécifiée ou un marqueur de fin spécial. La caractéristique de GreedyDecoding est qu’à chaque fois la probabilité conditionnelle actuelle est la meilleure
 Implémentation d'un modèle de diffusion de suppression du bruit à l'aide de PyTorch
Jan 14, 2024 pm 10:33 PM
Implémentation d'un modèle de diffusion de suppression du bruit à l'aide de PyTorch
Jan 14, 2024 pm 10:33 PM
Avant de comprendre en détail le principe de fonctionnement du modèle probabiliste de diffusion de débruitage (DDPM), comprenons d'abord une partie du développement de l'intelligence artificielle générative, qui est également l'une des recherches fondamentales du DDPM. VAEVAE utilise un encodeur, un espace latent probabiliste et un décodeur. Pendant l'entraînement, l'encodeur prédit la moyenne et la variance de chaque image et échantillonne ces valeurs à partir d'une distribution gaussienne. Le résultat de l'échantillonnage est transmis au décodeur, qui convertit l'image d'entrée sous une forme similaire à l'image de sortie. La divergence KL est utilisée pour calculer la perte. Un avantage significatif de la VAE est sa capacité à générer des images diversifiées. Lors de l'étape d'échantillonnage, on peut directement échantillonner à partir de la distribution gaussienne et générer de nouvelles images via le décodeur. Le GAN a fait de grands progrès dans le domaine des auto-encodeurs variationnels (VAE) en seulement un an.
 Tutoriel sur l'installation de PyCharm avec PyTorch
Feb 24, 2024 am 10:09 AM
Tutoriel sur l'installation de PyCharm avec PyTorch
Feb 24, 2024 am 10:09 AM
En tant que puissant framework d'apprentissage profond, PyTorch est largement utilisé dans divers projets d'apprentissage automatique. En tant que puissant environnement de développement intégré Python, PyCharm peut également fournir un bon support lors de la mise en œuvre de tâches d'apprentissage en profondeur. Cet article présentera en détail comment installer PyTorch dans PyCharm et fournira des exemples de code spécifiques pour aider les lecteurs à démarrer rapidement avec PyTorch pour des tâches d'apprentissage en profondeur. Étape 1 : Installer PyCharm Tout d’abord, nous devons nous assurer que nous avons
 si rapide! Reconnaissez la parole vidéo en texte en quelques minutes seulement avec moins de 10 lignes de code
Feb 27, 2024 pm 01:55 PM
si rapide! Reconnaissez la parole vidéo en texte en quelques minutes seulement avec moins de 10 lignes de code
Feb 27, 2024 pm 01:55 PM
Bonjour à tous, je m'appelle Kite. Il y a deux ans, le besoin de convertir des fichiers audio et vidéo en contenu texte était difficile à réaliser, mais il peut désormais être facilement résolu en quelques minutes seulement. On dit que pour obtenir des données de formation, certaines entreprises ont entièrement exploré des vidéos sur des plateformes vidéo courtes telles que Douyin et Kuaishou, puis ont extrait l'audio des vidéos et les ont converties sous forme de texte pour les utiliser comme corpus de formation pour les modèles Big Data. . Si vous devez convertir un fichier vidéo ou audio en texte, vous pouvez essayer cette solution open source disponible aujourd'hui. Par exemple, vous pouvez rechercher des moments précis où apparaissent des dialogues dans des programmes de cinéma et de télévision. Sans plus attendre, entrons dans le vif du sujet. Whisper est le Whisper open source d'OpenAI. Bien sûr, il est écrit en Python et ne nécessite que quelques packages d'installation simples.
 Apprentissage profond avec PHP et PyTorch
Jun 19, 2023 pm 02:43 PM
Apprentissage profond avec PHP et PyTorch
Jun 19, 2023 pm 02:43 PM
L’apprentissage profond est une branche importante dans le domaine de l’intelligence artificielle et a reçu de plus en plus d’attention ces dernières années. Afin de pouvoir mener des recherches et des applications en matière d'apprentissage profond, il est souvent nécessaire d'utiliser certains cadres d'apprentissage profond pour y parvenir. Dans cet article, nous présenterons comment utiliser PHP et PyTorch pour le deep learning. 1. Qu'est-ce que PyTorch ? PyTorch est un framework d'apprentissage automatique open source développé par Facebook. Il peut nous aider à créer et former rapidement des modèles d'apprentissage en profondeur. PyTorc
 Explication détaillée de GQA, le mécanisme d'attention couramment utilisé dans les grands modèles, et l'implémentation du code Pytorch
Apr 03, 2024 pm 05:40 PM
Explication détaillée de GQA, le mécanisme d'attention couramment utilisé dans les grands modèles, et l'implémentation du code Pytorch
Apr 03, 2024 pm 05:40 PM
Grouped Query Attention (GroupedQueryAttention) est une méthode d'attention multi-requêtes dans les grands modèles de langage. Son objectif est d'atteindre la qualité du MHA tout en maintenant la vitesse du MQA. GroupedQueryAttention regroupe les requêtes et les requêtes au sein de chaque groupe partagent le même poids d'attention, ce qui permet de réduire la complexité de calcul et d'augmenter la vitesse d'inférence. Dans cet article, nous expliquerons l'idée de GQA et comment la traduire en code. GQA est dans le document GQA:TrainingGeneralizedMulti-QueryTransformerModelsfromMulti-HeadCheckpoint





