Formes de base
SVG fournit de nombreuses formes de base. Ces éléments peuvent être utilisés directement, ce qui est bien mieux que la toile. Arrêtez de dire des bêtises et regardez directement l'exemple. C'est le plus direct :
Cet exemple dessine de nombreuses formes : rectangle normal, rectangle aux coins arrondis, cercle, ellipse, ligne droite, polyligne, polygone et chemin. Ce sont des éléments graphiques de base. Bien qu'il existe de nombreuses façons de dessiner un graphique, par exemple, un rectangle peut être implémenté en utilisant un rect ou un chemin, etc., nous devrions quand même essayer de garder le contenu du SVG court, concis et facile à lire .
Ce qui suit sont des instructions pour utiliser chaque forme (ici, nous introduisons uniquement les attributs de base qui contrôlent la forme et la position des graphiques, et les attributs tels que le remplissage seront résumés plus tard).
Rectangle - élément rectangle
Cet élément possède 6 attributs qui contrôlent la position et la forme, qui sont :
x : les coordonnées du coin supérieur gauche du rectangle (système de coordonnées utilisateur) x valeur.
y : La valeur y des coordonnées du coin supérieur gauche du rectangle (système de coordonnées utilisateur).
largeur : largeur du rectangle.
hauteur : hauteur du rectangle.
rx : Lors de l'obtention de l'effet de coin arrondi, le rayon du coin arrondi le long de l'axe x.
ry : Lors de l'obtention de l'effet de coin arrondi, le rayon du coin arrondi le long de l'axe y.
Par exemple, dans l'exemple ci-dessus, l'effet de coin arrondi est obtenu. Vous pouvez également obtenir l'effet de coin elliptique en définissant rx et ry sur des valeurs différentes.
Cercle - élément de cercle
Les attributs de cet élément sont très simples, définissant principalement le centre et le rayon du cercle :
r : le rayon du cercle.
cx : valeur x de la coordonnée du centre du cercle.
cy : valeur y de la coordonnée du centre du cercle.
Ellipse - élément ellipse
Il s'agit d'un élément circulaire plus général. Vous pouvez contrôler la longueur du demi-grand axe et du demi-petit axe séparément pour réaliser différents. ellipses, il est facile de penser que lorsque les deux demi-axes sont égaux, c'est un cercle parfait.
rx : demi-grand axe (rayon x).
ry : axe semi-mineur (rayon y).
cx : valeur x de la coordonnée du centre du cercle.
cy : valeur y de la coordonnée du centre du cercle.
Ligne droite - élément de ligne
Une ligne droite doit définir le point de départ et le point d'arrivée :
x1 : coordonnée x du point de départ.
y1 : coordonnée y du point de départ.
x2 : coordonnée x du point final.
y2 : coordonnée y du point final.
Polyline - élément polyligne
Polyline définit principalement les extrémités de chaque segment de ligne, donc seule une collection de points est nécessaire comme paramètre :
points : Une série de points séparés par des espaces, des virgules, des nouvelles lignes, etc. Chaque point doit avoir 2 nombres : valeur x et valeur y. Ainsi les trois points suivants (0,0), (1,1) et (2,2) peuvent s'écrire : "0 0, 1 1, 2 2".
Polygone - élément polygone
Cet élément fait une étape de plus que l'élément polyligne, reliant le dernier point au premier point pour former une figure fermée. Les paramètres sont les mêmes.
points : Une série de points séparés par des espaces, des virgules, des nouvelles lignes, etc. Chaque point doit avoir 2 nombres : valeur x et valeur y. Ainsi les trois points suivants (0,0), (1,1) et (2,2) peuvent s'écrire : "0 0, 1 1, 2 2".
Chemin - élément de chemin
C'est l'élément le plus polyvalent et le plus puissant ; en utilisant cet élément, vous pouvez réaliser n'importe quel autre graphique, non seulement la forme de base ci-dessus peut également être réalisée. des formes complexes comme les courbes de Bézier ; de plus, l'utilisation d'un chemin peut obtenir des segments de ligne de transition fluides. Bien que la polyligne puisse également être utilisée pour obtenir cet effet, de nombreux points doivent être fournis et l'effet d'agrandissement n'est pas bon. Cet élément contrôle la position et la forme avec un seul paramètre :
d : une série d'instructions de dessin et de paramètres de dessin (points) combinés.
Les instructions de dessin sont divisées en deux types : les instructions de coordonnées absolues et les instructions de coordonnées relatives. Les lettres utilisées dans ces deux instructions sont les mêmes, mais les instructions absolues utilisent des lettres majuscules et les coordonnées sont également absolues. coordonnées ; les instructions relatives utilisent les lettres minuscules correspondantes et les coordonnées des points représentent les décalages.
Instructions de dessin de coordonnées absolues
Les paramètres de ce groupe d'instructions représentent des coordonnées absolues. En supposant que la position actuelle du pinceau est (x0, y0), la signification des instructions de coordonnées absolues suivantes est la suivante :
| 指令 | 参数 | 说明 |
| M | x y | 将画笔移动到点(x,y) |
| L | x y | 画笔从当前的点绘制线段到点(x,y) |
| H | x | 画笔从当前的点绘制水平线段到点(x,y0) |
| V | y | 画笔从当前的点绘制竖直线段到点(x0,y) |
| A | rx ry x-axis-rotation large-arc-flag sweep-flag x y | 画笔从当前的点绘制一段圆弧到点(x,y) |
| C | x1 y1, x2 y2, x y | 画笔从当前的点绘制一段三次贝塞尔曲线到点(x,y) |
| S | x2 y2, x y | 特殊版本的三次贝塞尔曲线(省略第一个控制点) |
| Q | x1 y1, x y | 绘制二次贝塞尔曲线到点(x,y) |
| T | x y | 特殊版本的二次贝塞尔曲线(省略控制点) |
| Z | 无参数 | 绘制闭合图形，如果d属性不指定Z命令，则绘制线段，而不是封闭图形。 |
Commande de dessin d'arc : A rx ry x-axis-rotation large-arc-flag scanning-flag x y
Utiliser un arc pour connecter 2 points est plus compliqué et il existe de nombreuses situations, donc cette La commande dispose de 7 paramètres, qui contrôlent divers attributs de la courbe. Ce qui suit explique la signification des valeurs :
rx,ry est la longueur du demi-grand axe et du demi-petit axe de l'arc
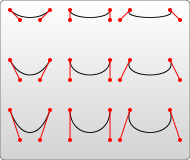
x-axis-rotation est l'angle entre l'axe des x où ceci L'arc est situé et la direction horizontale, c'est-à-dire l'axe des x. L'angle de rotation dans le sens inverse des aiguilles d'une montre, le nombre négatif représente l'angle de rotation dans le sens des aiguilles d'une montre.
large-arc-flag vaut 1 pour les arcs à grand angle et 0 pour les arcs à petit angle.
Le drapeau de balayage est 1, ce qui signifie que l'arc est dans le sens des aiguilles d'une montre autour du centre du point de départ au point final, et 0, qui est le sens dans le sens inverse des aiguilles d'une montre.
x,y sont les coordonnées terminales de l'arc.
Je n'entrerai pas dans les détails sur les deux premiers paramètres et les deux derniers paramètres, ils sont très simples ; parlons des trois paramètres du milieu :
la rotation de l'axe x représente l'angle de rotation. arc dans l'exemple ci-dessous La différence :
Vous pouvez voir sur l'image que les différents paramètres de rotation de l'ellipse conduisent à des directions différentes des arcs dessinés. Bien entendu, ce paramètre n'a aucun effet sur un cercle parfait.
large-arc-flag et scanning-flag contrôlent la taille et la direction de l'arc. Découvrez la différence des arcs dans les exemples suivants :
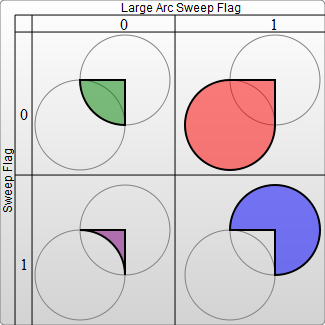
Comme le montre ce qui précède, ces paramètres sont en fait les seuls paramètres nécessaires pour déterminer un arc. On voit aussi ici que les arcs en SVG sont plus compliqués que ceux en canevas.
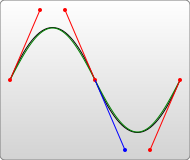
Instructions pour tracer la courbe de Bézier cubique : C x1 y1, x2 y2, x y
De ce qui précède, nous pouvons voir que les points de contrôle contrôlent l'arc de la courbe.
Version spéciale de la courbe de Bézier cubique : S x2 y2, x y
Souvent, afin de tracer une courbe lisse, il est nécessaire de tracer la courbe plusieurs fois en continu. À ce stade, afin de faciliter la transition, le point de contrôle de la deuxième courbe est souvent le point de cartographie du premier point de contrôle de la courbe de l'autre côté de la courbe. Cette version simplifiée peut être utilisée à ce moment. Ce qu'il faut noter ici, c'est que s'il n'y a pas d'autre commande S ou commande C avant la commande S, les deux points de contrôle seront considérés comme identiques à cet instant et dégénéreront en une courbe de Bézier quadratique si la commande S est utilisée ; dans un autre Après la commande S ou la commande C, le premier point de contrôle de la commande S suivante sera défini par défaut sur un point de cartographie du deuxième point de contrôle de la courbe précédente Essayez-le :
La commande S ci-dessus n'a que le deuxième point de contrôle, et le premier point de contrôle utilise un point de mappage du deuxième point de contrôle de la commande de courbe précédente.
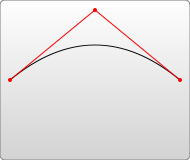
Instructions pour dessiner la courbe de Bézier quadratique : Q x1 y1, x y, T x y (version spéciale de la courbe de Bézier quadratique)
Courbe de Bézier quadratique uniquement Un point de contrôle (x1, y1) , généralement comme indiqué ci-dessous :
Si vous dessinez une courbe continue, vous pouvez également utiliser la version simplifiée T. De même, lorsque T est précédé d'une commande Q ou T, le point de contrôle de la commande T suivante sera défini par défaut sur le point de cartographie du point de contrôle de la courbe précédente. Essayez-le :
<.>
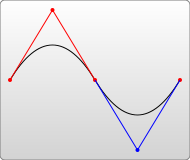
De même, si la commande T n'est pas précédée d'une commande Q ou T, on considère qu'il n'y a pas de point de contrôle et une ligne droite est tracée.
Les instructions de dessin de coordonnées relatives
ont les mêmes lettres que les instructions de dessin de coordonnées absolues, sauf qu'elles sont toutes en minuscules. Les paramètres impliquant des coordonnées dans les paramètres de cet ensemble d'instructions représentent des coordonnées relatives, ce qui signifie que les paramètres représentent le décalage du point actuel au point cible. Un nombre positif représente un décalage positif par rapport à l'axe et un nombre négatif représente un. décalage inverse. Cependant, pour la commande Z, il n’y a aucune différence entre les majuscules et les minuscules.
les instructions de coordonnées absolues et les instructions de coordonnées relatives peuvent être mélangées . Parfois, le mélange peut conduire à des méthodes de peinture plus flexibles.
Remarques sur le dessin du chemin SVG :
Lorsque vous dessinez des graphiques avec des trous, veuillez noter : les bords extérieurs doivent être dessinés dans le sens inverse des aiguilles d'une montre et les bords intérieurs du trous L'ordre doit être dans le sens des aiguilles d'une montre. Ce n'est qu'ainsi que l'effet de remplissage des graphiques dessinés sera correct.
Référence pratique : Index du script :
http://msdn.microsoft.com/zh-cn/library/ff971910(v=vs.85).aspx Centre de développement :
https://developer.mozilla.org/en/SVGRéférence populaire :
http://www.chinasvg.com/ Documentation officielle :
http://www.w3.org/TR/SVG11/
Méthode de récupération de données informatiques Xiaomi
Comment faire une image ronde en ppt
tutoriel de flexibilité
Que veut dire Kappa ?
La différence entre la version familiale Win10 et la version professionnelle
Comment entrer en mode de récupération sur un ordinateur Windows 10
Explication détaillée de la configuration de nginx
c'est-à-dire que le raccourci ne peut pas être supprimé
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
