 interface Web
interface Web
 Tutoriel H5
Tutoriel H5
 Tutoriel de dessin sur toile html5 (8) — méthode bezierCurveTo pour dessiner des courbes dans les compétences du didacticiel canvas_html5
Tutoriel de dessin sur toile html5 (8) — méthode bezierCurveTo pour dessiner des courbes dans les compétences du didacticiel canvas_html5
Tutoriel de dessin sur toile html5 (8) — méthode bezierCurveTo pour dessiner des courbes dans les compétences du didacticiel canvas_html5
Dans l'article précédent, j'ai parlé de trois méthodes pour dessiner des courbes dans Canvas : arc, arcTo et quadraticCurveTo. Elles ont toutes une chose en commun, c'est-à-dire. c'est-à-dire que les courbes que vous dessinez ne peuvent aller que d'un côté. La plus grande différence entre le bezierCurveTo dont nous parlons aujourd'hui et eux est qu'il a deux points de contrôle, ce qui signifie que vous pouvez dessiner une courbe en forme de S.
bezierCurveTo, également connue sous le nom de courbe de Bézier, si vous avez appris certains outils de dessin, vous pouvez le comprendre immédiatement.
La syntaxe de bezierCurveTo est la suivante :
ctx.bezierCurveTo(x1,y1,x2,y2,x,y); Je vais vous expliquer ses paramètres comme d'habitude, (x1,y1) ; est Les coordonnées du point de contrôle 1, (x2, y2) sont les coordonnées du point de contrôle 2 et (x, y) sont les coordonnées de son point final. Comme quadraticCurveTo, ses coordonnées de point de départ sont également prédéfinies par moveTo.
Donc, bezierCurveTo a besoin de 4 points pour tracer une courbe : point de départ, point final, point de contrôle 1, point de contrôle 2. Pour les besoins de l'explication ultérieure, je suppose ici que le point de contrôle 1 correspond au point de départ , et le point de contrôle 2 correspond au point final
Ici, nous devons mentionner à nouveau le vieux problème du dessin sur toile, c'est-à-dire que le dessin de code est entièrement basé sur des suppositions, et vous devez actualiser pour savoir où dessiner.
Je vais continuer la bonne tradition d'avant et tracer quelques lignes auxiliaires pour aider tout le monde à comprendre :
var x1=450, //coordonnée x du point de contrôle 1
y1 = 300, //y du point de contrôle 1
x2 = 450, // x du point de contrôle 2
y2 = 500, // y du point de contrôle 2
x = 300, // point final x
y = 500; // point final y
ctx.moveTo(300,300) ;//Point de départ
ctx.beginPath();
ctx.lineWidth = 5;
ctx.strokeStyle = "rgba(0,0,0,1)"
ctx.moveTo(300,300) ;
ctx.bezierCurveTo(x1,y1,x2,y2,x,y);
ctx.stroke(
//Commencer à dessiner des lignes auxiliaires
ctx); .beginPath();
ctx.strokeStyle = "rgba(255,0,0,0.5)";
ctx.lineWidth = 1;
// Connectez le point de départ et le point de contrôle 1
ctx.moveTo(300,300);
ctx.lineTo(x1,y1);
// Connectez le point final et le point de contrôle 2
ctx.moveTo(x2,y2); (x,y);
// Connectez le point de départ et le point final (ligne de base)
ctx.moveTo(300,300);
ctx.lineTo(x,y); )
 Ici, nous dessinons d'abord une courbe similaire à quadraticCurveTo, penchée uniquement d'un côté. Cette ligne semble « lisse » car les coordonnées x des points de contrôle 1 et 2 sont les mêmes.
Ici, nous dessinons d'abord une courbe similaire à quadraticCurveTo, penchée uniquement d'un côté. Cette ligne semble « lisse » car les coordonnées x des points de contrôle 1 et 2 sont les mêmes.
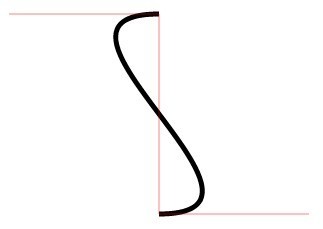 En fait, changez simplement les coordonnées du point de contrôle 1. Si les coordonnées du point de contrôle 1 et du point de contrôle 2 se trouvent des deux côtés de la ligne de base, une courbe en forme de S sera dessinée ; si elles sont toutes deux d'un côté de la ligne de base, elle aura un effet similaire à quadraticCurveTo.
En fait, changez simplement les coordonnées du point de contrôle 1. Si les coordonnées du point de contrôle 1 et du point de contrôle 2 se trouvent des deux côtés de la ligne de base, une courbe en forme de S sera dessinée ; si elles sont toutes deux d'un côté de la ligne de base, elle aura un effet similaire à quadraticCurveTo.
Chaque méthode de dessin semble avoir une fonction relativement unique, mais les méthodes puissantes sont la combinaison de méthodes individuelles. Dans les articles suivants, j'essaierai d'expliquer comment dessiner certains graphiques conventionnels, tels que des rectangles arrondis et des ellipses. Ils nécessitent une combinaison de ces méthodes simples précédentes.

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Quelles écoles utilisent la toile ?
Aug 18, 2023 pm 05:59 PM
Quelles écoles utilisent la toile ?
Aug 18, 2023 pm 05:59 PM
Les écoles utilisant Canvas comprennent l'Université de Stanford, le MIT, l'Université de Columbia, l'Université de Californie, Berkeley, etc. Introduction détaillée : 1. L'Université de Stanford utilise Canvas comme principale plate-forme d'apprentissage en ligne. Les enseignants et les étudiants de l'Université de Stanford utilisent Canvas pour gérer et communiquer le contenu des cours et apprendre grâce à des fonctions telles que les discussions en ligne, les soumissions de devoirs et les examens. L'Institut polytechnique et le MIT utilisent également Canvas comme système de gestion de l'apprentissage en ligne et gèrent les cours via la plateforme Canvas 3. Columbia University, etc.
 Que sont les plug-ins de flèches de canevas ?
Aug 21, 2023 pm 02:14 PM
Que sont les plug-ins de flèches de canevas ?
Aug 21, 2023 pm 02:14 PM
Les plug-ins de flèches du canevas incluent : 1. Fabric.js, qui possède une API simple et facile à utiliser et peut créer des effets de flèche personnalisés ; 2. Konva.js, qui fournit la fonction de dessiner des flèches et peut créer diverses flèches ; styles ; 3. Pixi.js, qui fournit des fonctions de traitement graphique riches et peut obtenir divers effets de flèche ; 4. Two.js, qui peut facilement créer et contrôler des styles de flèches et des animations 5. Arrow.js, qui peut créer divers effets de flèche ; ; 6. Rough .js, vous pouvez créer des flèches dessinées à la main, etc.
 Quels sont les détails de l'horloge en toile ?
Aug 21, 2023 pm 05:07 PM
Quels sont les détails de l'horloge en toile ?
Aug 21, 2023 pm 05:07 PM
Les détails de l'horloge sur toile incluent l'apparence de l'horloge, les graduations, l'horloge numérique, les aiguilles des heures, des minutes et des secondes, le point central, les effets d'animation, d'autres styles, etc. Introduction détaillée : 1. Apparence de l'horloge, vous pouvez utiliser Canvas pour dessiner un cadran circulaire comme apparence de l'horloge, et vous pouvez définir la taille, la couleur, la bordure et d'autres styles du cadran 2. Lignes d'échelle, tracez des lignes d'échelle dessus ; le cadran pour représenter les heures ou les minutes. Position ; 3. Horloge numérique, vous pouvez dessiner une horloge numérique sur le cadran pour indiquer l'heure et les minutes actuelles ; 4. Aiguille des heures, aiguille des minutes, aiguille des secondes, etc.
 Quelles versions de html2canvas existe-t-il ?
Aug 22, 2023 pm 05:58 PM
Quelles versions de html2canvas existe-t-il ?
Aug 22, 2023 pm 05:58 PM
Les versions de html2canvas incluent html2canvas v0.x, html2canvas v1.x, etc. Introduction détaillée : 1. html2canvas v0.x, qui est une première version de html2canvas. La dernière version stable est la v0.5.0-alpha1. Il s'agit d'une version mature qui a été largement utilisée et vérifiée dans de nombreux projets ; 2. html2canvas v1.x, il s'agit d'une nouvelle version de html2canvas.
 Apprenez le cadre de canevas et expliquez en détail le cadre de canevas couramment utilisé
Jan 17, 2024 am 11:03 AM
Apprenez le cadre de canevas et expliquez en détail le cadre de canevas couramment utilisé
Jan 17, 2024 am 11:03 AM
Explorez le framework Canvas : Pour comprendre quels sont les frameworks Canvas couramment utilisés, des exemples de code spécifiques sont nécessaires. Introduction : Canvas est une API de dessin fournie en HTML5, grâce à laquelle nous pouvons obtenir des graphiques et des effets d'animation riches. Afin d'améliorer l'efficacité et la commodité du dessin, de nombreux développeurs ont développé différents frameworks Canvas. Cet article présentera certains frameworks Canvas couramment utilisés et fournira des exemples de code spécifiques pour aider les lecteurs à mieux comprendre comment utiliser ces frameworks. 1.Cadre EaselJSEa
 uniapp implémente comment utiliser Canvas pour dessiner des graphiques et des effets d'animation
Oct 18, 2023 am 10:42 AM
uniapp implémente comment utiliser Canvas pour dessiner des graphiques et des effets d'animation
Oct 18, 2023 am 10:42 AM
Comment utiliser Canvas pour dessiner des graphiques et des effets d'animation dans Uniapp nécessite des exemples de code spécifiques 1. Introduction Avec la popularité des appareils mobiles, de plus en plus d'applications doivent afficher divers graphiques et effets d'animation sur le terminal mobile. En tant que framework de développement multiplateforme basé sur Vue.js, uniapp offre la possibilité d'utiliser un canevas pour dessiner des graphiques et des effets d'animation. Cet article présentera comment Uniapp utilise Canvas pour obtenir des effets de graphique et d'animation, et donnera des exemples de code spécifiques. 2. toile
 Quelles sont les propriétés de la toile tkinter ?
Aug 21, 2023 pm 05:46 PM
Quelles sont les propriétés de la toile tkinter ?
Aug 21, 2023 pm 05:46 PM
Les attributs du canevas tkinter incluent bg, bd, relief, width, height, curseur, highlightbackground, highlightcolor, highlightthickness, insertbackground, insertwidth, selectbackground, selectforeground, les attributs xscrollcommand, etc. Présentation détaillée
 Explorez le rôle puissant et l'application du canevas dans le développement de jeux
Jan 17, 2024 am 11:00 AM
Explorez le rôle puissant et l'application du canevas dans le développement de jeux
Jan 17, 2024 am 11:00 AM
Comprendre la puissance et l'application du canevas dans le développement de jeux Présentation : Avec le développement rapide de la technologie Internet, les jeux Web deviennent de plus en plus populaires parmi les joueurs. En tant qu'élément important du développement de jeux Web, la technologie Canvas a progressivement émergé dans le développement de jeux, démontrant sa puissance et ses applications puissantes. Cet article présentera le potentiel du canevas dans le développement de jeux et démontrera son application à travers des exemples de code spécifiques. 1. Introduction à la technologie Canvas Canvas est un nouvel élément HTML5 qui nous permet d'utiliser





