Calculer l'intersection du carré de la courbe y=x et de la droite x=1 en Java par récursion

Utilisez la méthode récursive en Java pour calculer le carré de la courbe y x et le bord incurvé entouré par la droite x 1 axe x

classe publique Util {

public static void main(String[] args) {

System.out.println(getMj(2000));

}

public statique double calculateArea(double n){

si(n==1){

retour 1.0 ;

}autre{

double r = (n-1) * (n-1) * (n+1) * (2*n+1) / (n * n * n * (2*n-1));

retour r*getMj(n-1);

}

}

}

La condition préalable à l'algorithme récursif est de comprendre sa formule générale 2000 signifie diviser le triangle courbe en 2000 rectangles. Le principe spécifique est visible dans la figure ci-dessous :

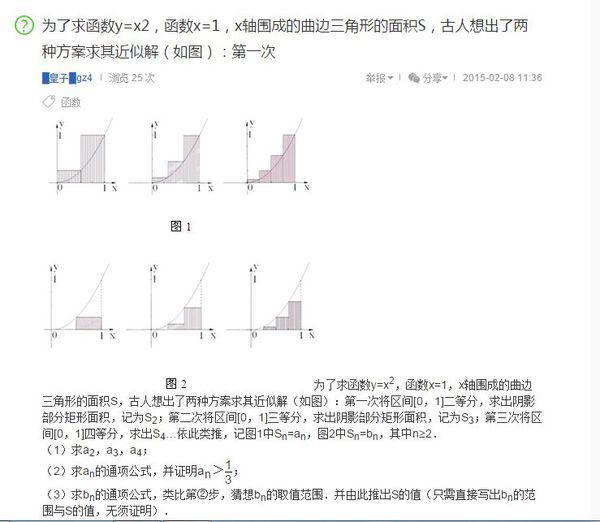
En utilisant l'algorithme de la figure 1 :

an=(n+1)(2n+1) /6n^2

La façon simple de l'écrire est la suivante :

classe publique Util {

public static void main(String[] args) {

System.out.println(getMj(100000));

}

public statique double calculateArea(double n){

retour (n+1)*(2*n+1)/(6*n*n);

}

}

Problème de récursion Java

(1) La récursivité s'appelle dans une procédure ou une fonction

 ;

(2) Lorsque vous utilisez une stratégie récursive, vous devez vous assurer qu'il existe une condition de fin de récursion claire, également connue sous le nom de sortie récursive.

Les algorithmes récursifs sont généralement utilisés pour résoudre trois types de problèmes :

(1) La définition des données est définie de manière récursive. (Fonction Fibonacci)

(2) La solution du problème est implémentée selon l'algorithme récursif. (Retraçage)

(3) La forme structurelle des données est définie de manière récursive.

L'exemple suivant calcule la factorielle de n de manière récursive.

Test en classe publique {

public static int factoriel(int n) {

si(n == 0){

retour 1;

}autre{

retour n * factoriel(n-1);

}

}

public static void main(String[] args) {

System.out.println(factorial(3));

}

}

L'algorithme récursif de réduction de moitié de la recherche dans la structure de données Java nécessite les conseils d'un expert !

source du colis ;

Recherche de classe publique {

Recherche binaire booléenne statique publique (int[] a, int x, int gauche, int droite) { // Méthode principale de recherche binaire //... }

if (x == a[gauche] || x == a[droite]) { return true; // Trouvé, renvoie true }

Si le résultat de (droite-gauche) est un nombre négatif, cela signifie que la valeur de droite est inférieure à la valeur de gauche. .

int mid = (gauche+droite)/2; //sinon : deux points

if(x == a[mid]) return true; // Trouve l'élément du milieu et renvoie true

sinon{ //sinon

Si x est supérieur à l'élément du milieu, renvoyez la fonction de recherche binaire (binarySearch) et continuez à rechercher x dans la moitié droite du tableau (a), c'est-à-dire binaireSearch(a,x,mid+1,right) . Cela peut restreindre la portée de la recherche et améliorer l’efficacité de la recherche.

else return binaireSearch(a, x, left, mid-1); // Si la valeur cible est inférieure à l'élément du milieu, continuez la recherche dans la moitié gauche.

}

}

public static final int[] sort(int[] a) { // Il s'agit d'une méthode utilisée pour trier un tableau d'entiers // Vous pouvez utiliser n'importe quel algorithme de tri, tel que le tri à bulles, le tri par insertion, le tri par sélection, le tri rapide, etc. // Ici, nous utilisons le tri à bulles pour trier le tableau pour (int i = 0; i a[j + 1]) { // Permuter les positions des éléments int temp = a[j];

for (int i = 0; i

for (int j = 0; j

si(a[i]

échanger(a,i,j);

}

}

}

retourner un ;

}

private static void swap(int[] a, int i, int j) { //Définissez un swap de fonction statique privé pour échanger les positions des éléments indicés i et j dans le tableau a

int temp = a[i];

a[i] = a[j];

a[j] = temp;

}

public static void print(int[] a) { //Fonction d'impression pour (int i = 0; i

System.out.println();

for (int i = 0; i

System.out.print(a[i]);

if(i!=a.length-1) { System.out.print(","); }

}

System.out.println();

}

public static void main(String[] args) { //Méthode de test

int[] a = {90, 12, 21, 32, 51, 78, 87, 98} ; est un tableau contenant 8 entiers.

imprimer(trier(a));

System.out.println(binarySearch(sort(a), 40, 0, a.length-1)); est un code utilisé pour rechercher binairement des éléments d'une valeur de 40 dans le tableau trié a.

}

}

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!