Tutoriel de dessin sur toile html5 (6) : méthode arcTo pour dessiner des courbes dans les compétences du didacticiel canvas_html5

L'article précédent parlait de la méthode arc de canvas, et cet article parle de la méthode arcTo qui y est associée.
arc et arcTo sont similaires de par leurs noms. arcTo est également une méthode pour dessiner des courbes, et la courbe qu'il dessine est également un arc de cercle parfait. Mais ses paramètres sont tout simplement incompatibles avec arc~
ctx.arcTo(x1,y1,x2,y2,radius); Les paramètres de arcTo incluent deux points, et ces deux points ne représentent pas le centre du cercle. seul le dernier paramètre est le rayon du cercle, indiquant que arcTo a une relation avec le cercle.
Il y a très peu d'articles sur arcTo sur Internet, et j'en ai finalement trouvé un provenant d'un pays étranger ; et il n'y a pas d'outils intuitifs pour dessiner sur toile, donc je ne peux que deviner arcTo qui m'a fait deviner pendant longtemps. . .
Pour une description intuitive, j'ai adopté une méthode auxiliaire : partout où arcTo est dessiné, j'utilise également lineTo pour dessiner les points correspondants afin de voir leur relation. Tracez simplement des lignes auxiliaires.

Copier le code

Le code est le suivant :

var x0=100,
y0 =400,
x1 = 500,
y1 = 400,
x2 = 450,
y2 = 450;
ctx.beginPath(); x0,y0 );
ctx.StrokeStyle = "#f00";
ctx.lineWidth = 2;
ctx.arcTo(x1,y1,x2,y2,20); ();
ctx.beginPath();
ctx.StrokeStyle = "rgba(0,0,0,0.5)"
ctx.lineWidth = 1; y0);
ctx.lineTo(x1,y1);
ctx.fillText('x1,y1',x1 10,y1 10)
ctx.lineTo(x2,y2); .fillText( 'x2,y2',x2 10,y2)
ctx.stroke();


Cela ressemble à beaucoup de code, mais c'est en fait très simple. J'ai utilisé quelques variables pour enregistrer les valeurs de coordonnées, et le reste était des opérations sur le canevas.
Description de la variable : x0, y0 sont les coordonnées du point de départ, x1, y1 sont les coordonnées du premier point, x2, y2 sont les coordonnées du deuxième point. La ligne droite tracée par lineTo est une ligne noire translucide de 1 px et la ligne tracée par arcTo est une ligne rouge de 2 px.
Actualisez la page et vous verrez l'image ci-dessous.

Je dois dire que cette ligne rouge ressemble à un crochet.

Ensuite, la règle de arcTo est trouvée. Elle passe en fait par le point de départ, le premier point et les deux droites au deuxième point, formant un angle inclus, et ces deux droites sont également tangentes au cercle paramètre. Le rayon du cercle détermine où le cercle sera tangent à la ligne. Tout comme une balle roulant dans un point mort, plus la balle est petite, plus elle roule loin et plus près du point mort ; l’inverse est vrai pour une balle plus grosse ;

Il s’agit d’un problème académique très grave, ne soyez pas YY.
Agrandissons le ballon !





Copier le code

Le code est le suivant : ctx.arcTo(x1, y1,x2 ,y2,50); //Changez le rayon à 50

Comme le montre l'image, vous pouvez voir que l'arc est devenu très grand et n'est même plus tangent à la ligne droite.

Bien sûr, en fait elles sont toujours tangentes, car la ligne tangente s'étend à l'infini. Nous continuons à explorer, continuons à agrandir le cercle et raccourcissons la distance entre le point de départ et le premier point.

Copier le code

Le code est le suivant : var x0=400 ; /Point de départ x Les coordonnées passent de 100 à 400

...

ctx.arcTo(x1,y1,x2,y2,100); //Le rayon du cercle augmente jusqu'à 100 et alors vous verrez une forme si étrange.

C'était à l'origine un crochet, mais maintenant il s'est plié brusquement, et même dans le sens opposé ! C'est un peu comme un casier à bouteilles de vin.
Attention cependant, ce cercle est toujours tangent aux deux droites ! C'est juste que maintenant la longueur des deux lignes ne peut pas atteindre le cercle ! Il a étendu les deux lignes sans fil !

Quand cette poignée de crochet sera-t-elle inversée ? Si vous êtes bon en géométrie, vous pouvez essayer de comprendre l'équation tangente entre un point et un cercle. 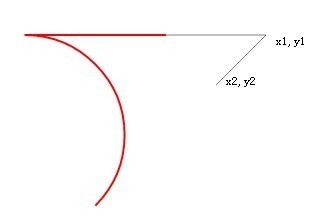Il y a un point très important dans la méthode arcTo. Ce point important est (x1, y1) dans le code tant que sa distance au point tangent du cercle dépasse sa distance au point de départ (x0, y0). ), Un renversement se produira.

On peut voir sur l'image que les coordonnées du point (x2, y2) peuvent changer à l'infini Tant qu'il s'agit toujours d'un point sur la tangente, alors lorsque le rayon du cercle reste inchangé, le graphique est tracé. par arcTo Rien ne changera. Cela nécessite une attention particulière.
Permettez-moi d'utiliser mes connaissances en géométrie qui ne sont pas disponibles sur la table pour vérifier cette proposition. Pour faciliter le calcul, je change d'abord l'angle entre les deux lignes à 90 degrés.





Copier le code

Le code est le suivant :

var x0=100,
y0=400,
x1 = 500,
y1 = 400,
x2 = 500,
y2 = 450; 🎜>
Après le changement, il ouvre à 90 degrés ! Nous gardons le rayon de la balle constant. Après rafraîchissement :

Nous agrandissons y2, c'est-à-dire prolongeons une ligne tangente et la transformons en 550. Après rafraîchissement :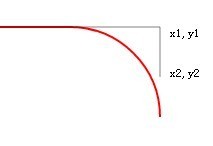

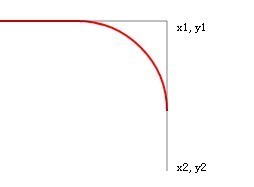La ligne tangente est prolongée, mais la ligne rouge tracée par arcTo n'a aucun changement.