Plus efficace que le mantra « Réfléchissons étape par étape », il rappelle que le projet s'améliore.

Les grands modèles de langage peuvent effectuer une ingénierie automatique d'indices via des méta-indices, mais leur potentiel peut ne pas être pleinement exploité en raison du manque de conseils suffisants pour guider les capacités de raisonnement complexes dans les grands modèles de langage. Alors comment guider de grands modèles de langage pour réaliser des projets d'invite automatiques ?

Les grands modèles de langage (LLM) sont des outils puissants dans les tâches de traitement du langage naturel, mais trouver des indices optimaux nécessite souvent de nombreux essais et erreurs manuels. En raison de la nature sensible du modèle, même après le déploiement en production, des cas extrêmes inattendus peuvent survenir nécessitant un réglage manuel supplémentaire pour améliorer les invites. Par conséquent, même si le LLM présente un grand potentiel, une intervention manuelle est toujours nécessaire pour optimiser ses performances dans les applications pratiques.

Ces défis ont donné naissance au domaine de recherche émergent de l’ingénierie automatique des invites. Une approche notable dans ce domaine consiste à tirer parti des propres capacités de LLM. Plus précisément, cela implique d'utiliser des instructions pour méta-repère LLM, telles que « vérifier l'invite actuelle et le lot d'échantillons, puis générer une nouvelle invite ».

Bien que ces méthodes atteignent des performances impressionnantes, la question qui se pose est la suivante : quels types de méta-indices sont adaptés à l'ingénierie des indices automatiques ?

Pour répondre à cette question, des chercheurs de l'Université de Californie du Sud et de Microsoft ont découvert deux observations clés. Premièrement, l’ingénierie rapide elle-même est une tâche linguistique complexe qui nécessite un raisonnement approfondi. Cela signifie examiner attentivement le modèle à la recherche d'erreurs, déterminer si certaines informations sont manquantes ou trompeuses dans l'invite actuelle et trouver des moyens de communiquer la tâche plus clairement. Deuxièmement, en LLM, les capacités de raisonnement complexes peuvent être stimulées en guidant le modèle pour qu'il réfléchisse étape par étape. Nous pouvons encore améliorer cette capacité en demandant au modèle de réfléchir à ses résultats. Ces observations fournissent des indices précieux pour résoudre ce problème.

Adresse papier : https://arxiv.org/pdf/2311.05661.pdf

Grâce aux observations précédentes, le chercheur a mené un projet de mise au point visant à établir un méta-indice pour effectuer plus efficacement l'ingénierie des indices pour LLM Fournir des conseils (voir la figure 2 ci-dessous). En réfléchissant aux limites des méthodes existantes et en intégrant les progrès récents dans les invites de raisonnement complexes, ils introduisent des composants de méta-indices tels que des modèles de raisonnement étape par étape et des spécifications de contexte pour guider explicitement le processus de raisonnement de LLM dans l'ingénierie des invites.

De plus, étant donné que l'ingénierie des indices est étroitement liée aux problèmes d'optimisation, nous pouvons nous inspirer de concepts d'optimisation courants tels que la taille du lot, la taille des pas et l'élan et les introduire dans des méta-indices pour des améliorations. Nous avons expérimenté ces composants et variantes sur deux ensembles de données d'inférence mathématique, MultiArith et GSM8K, et identifié une combinaison la plus performante, que nous avons nommée PE2.

PE2 a fait des progrès significatifs en termes de performances empiriques. En utilisant TEXT-DAVINCI-003 comme modèle de tâche, les invites générées par PE2 se sont améliorées de 6,3 % sur MultiArith et de 3,1 % sur GSM8K par rapport aux invites de réflexion étape par étape de la chaîne de réflexion zéro tir. De plus, PE2 surpasse les deux bases d'ingénierie d'invite automatique, à savoir l'APE et l'APO itératifs (voir Figure 1).

Il convient de noter que PE2 est plus efficace sur les tâches contrefactuelles. De plus, cette étude démontre la large applicabilité de PE2 pour optimiser les invites longues et réelles.

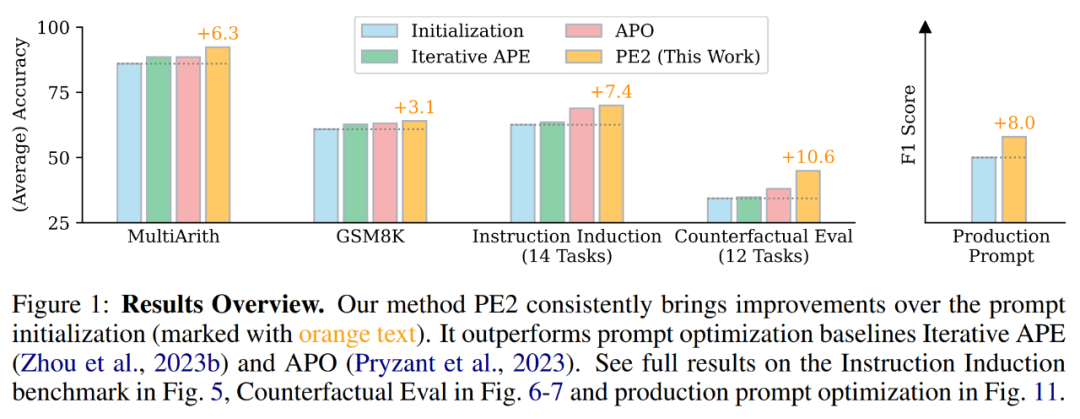
En examinant l'historique d'édition rapide de PE2, les chercheurs ont découvert que PE2 a toujours fourni une édition rapide significative. Il est capable de corriger les indices incorrects ou incomplets et de les enrichir en ajoutant des détails supplémentaires, ce qui entraîne une amélioration ultime des performances (indiquée dans le tableau 4).

Fait intéressant, lorsque PE2 ne connaît pas l'addition en octal, il établit ses propres règles arithmétiques à partir de l'exemple : "Si les deux nombres sont inférieurs à 50, ajoutez 2 à la somme. Si l'un des nombres est égal ou supérieur à 50, ajoutez 22 à la somme. » Bien qu’il s’agisse d’une solution imparfaite et simple, elle démontre la remarquable capacité de PE2 à raisonner dans des situations contrefactuelles.

Malgré ces réalisations, les chercheurs ont également reconnu les limites et les échecs du PE2. PE2 est également soumis à des limitations inhérentes à LLM, telles que la plausibilité d'ignorer les instructions données et de générer des erreurs (indiquées dans le tableau 5 ci-dessous).

Connaissances de base

Projet de conseils

L'objectif de l'ingénierie des invites est de trouver l'invite de texte p∗ qui obtient les meilleures performances sur un ensemble de données D donné lors de l'utilisation d'une M_task LLM donnée comme modèle de tâche (comme indiqué dans la formule suivante). Plus précisément, supposons que tous les ensembles de données puissent être formatés sous forme de paires d'entrée-sortie de texte, c'est-à-dire D = {(x, y)}. Un ensemble de formation D_train pour les conseils d'optimisation, un D_dev pour la validation et un D_test pour l'évaluation finale. Selon la représentation symbolique proposée par les chercheurs, le problème d'ingénierie rapide peut être décrit comme :

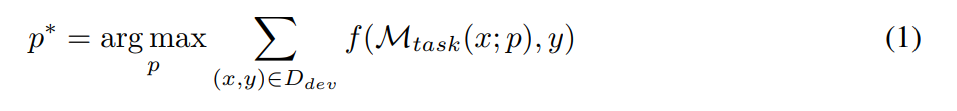
où, M_task (x; p) est la sortie générée par le modèle étant donné l'invite p, et f est pour chaque exemple fonction d’évaluation. Par exemple, si la métrique d'évaluation correspond exactement, alors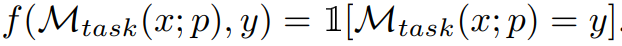

Utiliser LLM pour l'ingénierie des invites automatiques

Étant donné un ensemble initial d'invites, l'ingénieur d'invites automatiques proposera continuellement de nouvelles invites potentiellement meilleures. À l'horodatage t, l'ingénieur d'invite reçoit une invite p^(t) et s'attend à écrire une nouvelle invite p^(t+1). Lors de la génération d'un nouvel indice, on peut éventuellement examiner un lot d'exemples B = {(x, y, y′ )}. Ici, y ′ = M_task (x; p) représente la sortie générée par le modèle et y représente la véritable étiquette. Utilisez p^meta pour représenter une méta-invite qui guide M_proposal de LLM pour proposer de nouvelles propositions. Par conséquent,

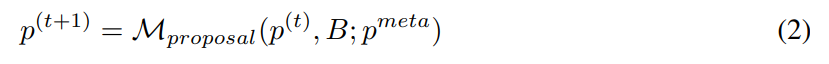
Construire un meilleur méta-repère p^meta pour améliorer la qualité de l'indice proposé p^(t+1) est l'objectif principal de cette étude.

Créer de meilleurs méta-indices

Tout comme les indices jouent un rôle important dans l'exécution de la tâche finale, le méta-indice p^meta introduit dans l'équation 2 joue un rôle important dans la qualité des indices nouvellement proposés et dans l'ensemble. la qualité de l’ingénierie des repères automatiques joue un rôle important.

Les chercheurs se concentrent principalement sur l'ingénierie des signaux méta-repère p^meta, ont développé des composants méta-repère qui peuvent aider à améliorer la qualité de l'ingénierie des signaux LLM et ont mené des études d'ablation systématique sur ces composants.

Les chercheurs ont conçu la base de ces composants sur la base des deux motivations suivantes : (1) Fournir des conseils détaillés et des informations de base ; (2) Incorporer des concepts d'optimisation communs ; Ensuite, les chercheurs décrivent ces éléments plus en détail et expliquent les principes sous-jacents. La figure 2 ci-dessous est une représentation visuelle.

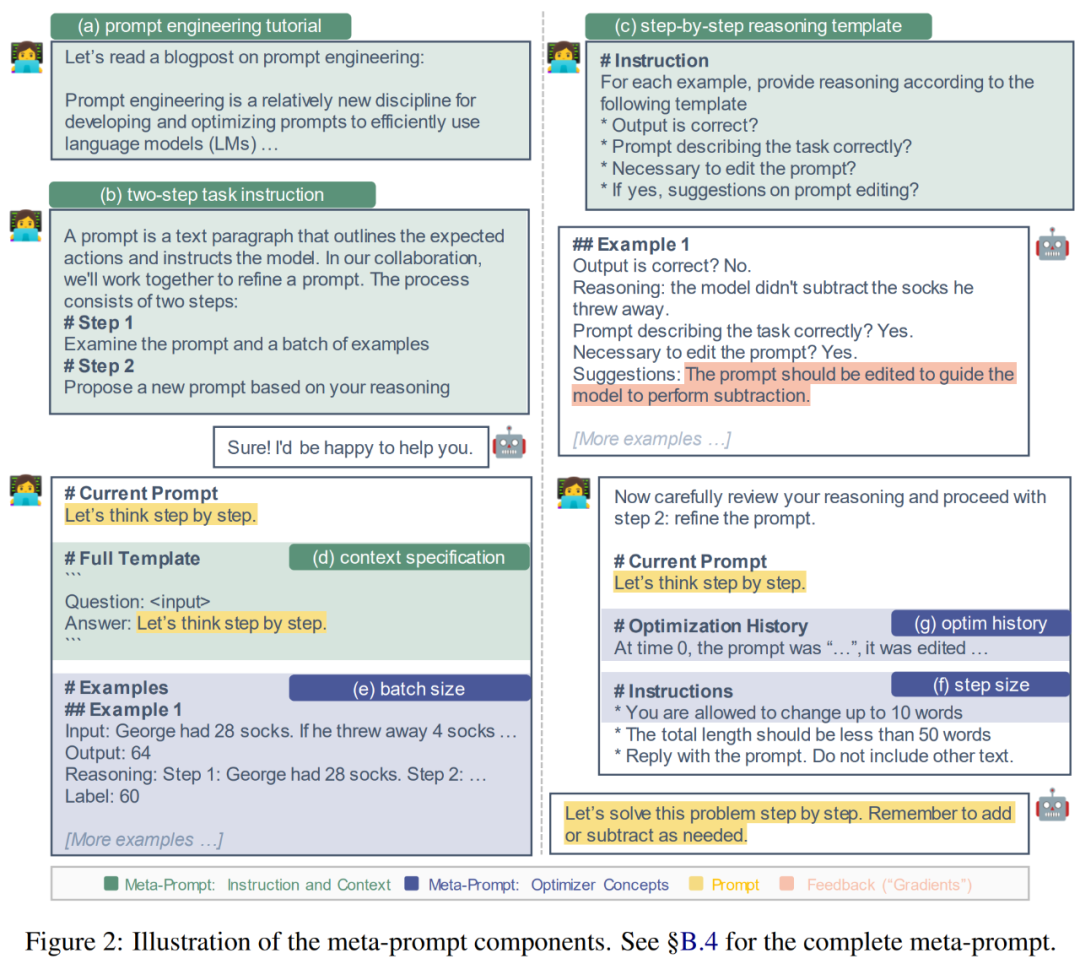
Fournit des instructions détaillées et un contexte. Dans des études précédentes, les méta-indices demandaient au modèle proposé de générer une paraphrase de l'invite ou contenaient des instructions minimales sur l'examen d'un lot d'exemples. Par conséquent, il peut être avantageux d’ajouter des instructions et un contexte supplémentaires aux méta-indices.

(a) Tutoriel d'ingénierie rapide. Afin d'aider LLM à mieux comprendre la tâche de l'ingénierie rapide, les chercheurs proposent un didacticiel en ligne sur l'ingénierie rapide dans les méta-indices.

(b) Description de la tâche en deux étapes. La tâche d'ingénierie des invites peut être décomposée en deux étapes, comme l'ont fait Pryzant et al. : Dans la première étape, le modèle doit examiner l'invite actuelle et un lot d'exemples. Dans la deuxième étape, le modèle doit créer une invite améliorée. Cependant, dans l'approche de Pryzant et al., chaque étape est expliquée à la volée. Au lieu de cela, les chercheurs ont envisagé de clarifier ces deux étapes dans le métacue et de transmettre les attentes à l'avance.

(c) Modèle de raisonnement étape par étape. Pour encourager le modèle à examiner attentivement chaque exemple du lot B et à réfléchir aux limites de l'invite actuelle, nous avons guidé le modèle de proposition d'invite M_proposal pour répondre à une série de questions. Par exemple : le résultat est-il correct ? L'invite décrit-elle correctement la tâche ? Est-il nécessaire de modifier l'invite ?

(d) Spécification du contexte. En pratique, il existe une flexibilité quant à l'endroit où les indices sont insérés tout au long de la séquence d'entrée. Il peut décrire la tâche avant de saisir le texte, par exemple « Traduire l'anglais vers le français ». Il peut également apparaître après la saisie d'un texte, comme « réfléchir étape par étape » pour déclencher des capacités de raisonnement. Pour reconnaître ces différents contextes, les chercheurs précisent explicitement l’interaction entre les signaux et les entrées. Par exemple : "Q : A : Réfléchissez étape par étape."

Incorporez les concepts d'optimisation courants. Le problème d'ingénierie des signaux décrit précédemment dans l'équation 1 est essentiellement un problème d'optimisation, tandis que la proposition de signaux dans l'équation 2 peut être considérée comme subissant une étape d'optimisation. Par conséquent, les chercheurs considèrent les concepts suivants couramment utilisés dans l’optimisation basée sur le gradient et développent leurs homologues pour les utiliser dans les méta-indices.

(e) Taille du lot. La taille du lot correspond au nombre d'exemples (en échec) utilisés dans chaque étape de proposition de pourboire (équation 2). Les auteurs ont essayé des tailles de lots de {1, 2, 4, 8} dans leur analyse.

(f) taille du pas. Dans l'optimisation basée sur le gradient, la taille du pas détermine le degré de mise à jour des pondérations du modèle. Dans un projet d'invite, sa contrepartie peut être le nombre de mots (jetons) pouvant être modifiés. L'auteur précise directement "Vous pouvez modifier jusqu'à s mots dans l'invite d'origine", où s ∈ {5, 10, 15, Aucun}.

(g) Optimiser l'histoire et la dynamique. Momentum (Qian, 1999) est une technique qui accélère l'optimisation et évite les oscillations en maintenant une moyenne mobile des gradients passés. Pour développer la contrepartie linguistique de momentum, cet article comprend un résumé de toutes les invites passées (horodatées 0, 1, ..., t − 1), leurs performances sur l'ensemble de développement et les modifications des invites.

Expérience

Les auteurs ont utilisé les quatre ensembles de tâches suivants pour évaluer l'efficacité et les limites du PE2 :

1. Raisonnement mathématique ; 2. Introduction pédagogique ; 3. Évaluation contrefactuelle ;

Benchmarks améliorés et LLM mis à jour. Dans les deux premières parties du tableau 2, les auteurs observent des améliorations significatives des performances en utilisant TEXT-DAVINCI-003, indiquant qu'il est plus capable de résoudre des problèmes de raisonnement mathématique dans Zero-shot CoT. De plus, l'écart entre les deux signaux a diminué (MultiArith : 3,3 % → 1,0 %, GSM8K : 2,3 % → 0,6 %), indiquant une sensibilité réduite de TEXT-DAVINCI-003 à l'interprétation des signaux. Pour cette raison, les méthodes qui reposent sur des paraphrases simples, telles que l’APE itérative, peuvent ne pas être efficaces pour améliorer les résultats finaux. Une édition rapide plus précise et ciblée est nécessaire pour améliorer les performances.

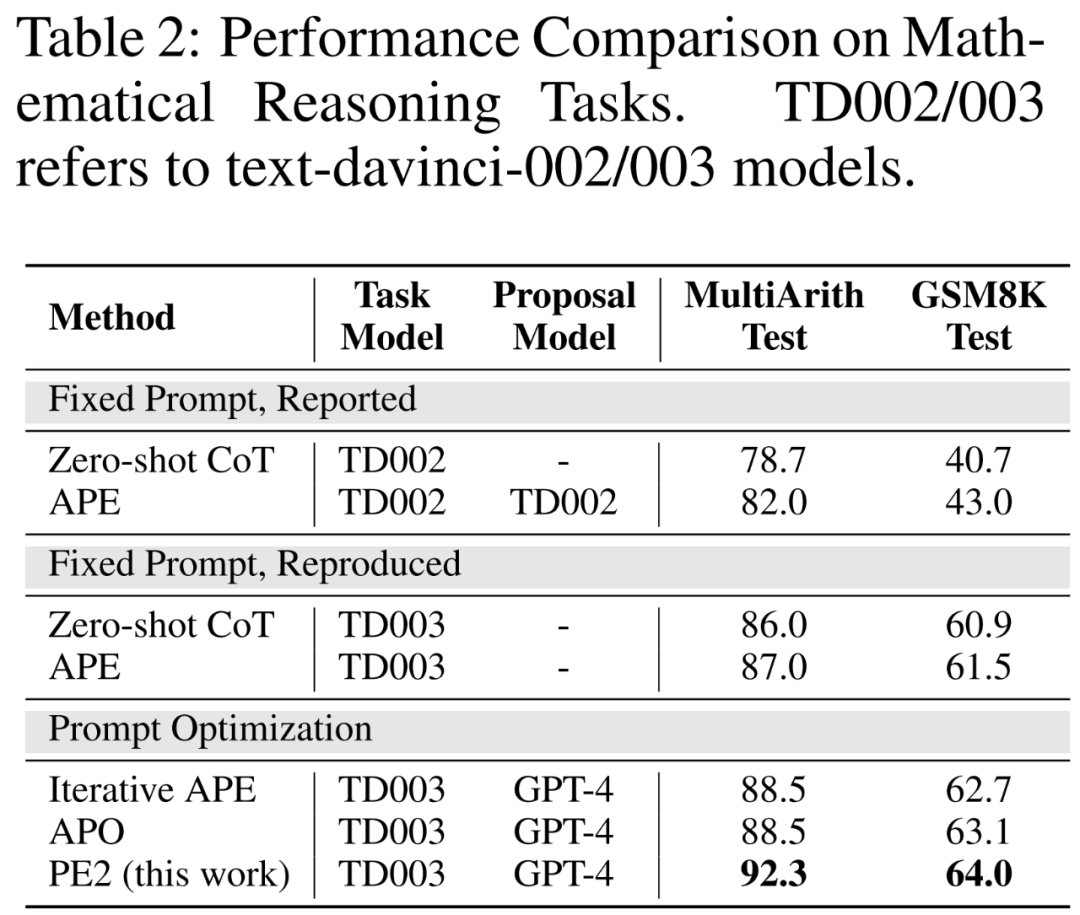
PE2 surpasse les APE et APO itératifs sur diverses tâches. PE2 est capable de trouver une pointe avec une précision de 92,3 % sur MultiArith (6,3 % de mieux que Zero-shot CoT) et de 64,0 % sur GSM8K (+3,1 %). De plus, PE2 a trouvé des indices qui surpassaient l'APE itératif et l'APO sur le test d'induction des instructions, l'évaluation contrefactuelle et les indices de production.

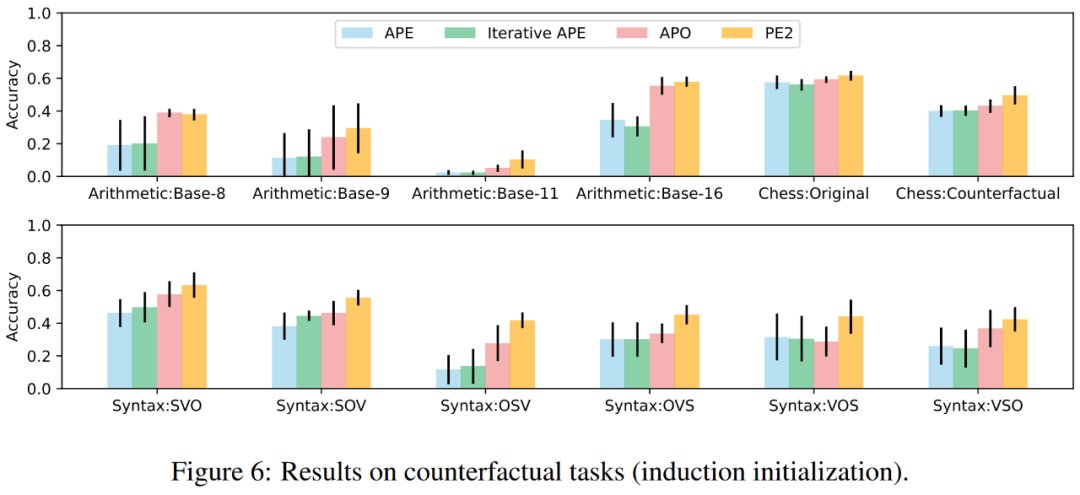
Dans la figure 1 ci-dessus, l'auteur résume les améliorations de performances obtenues par PE2 sur le benchmark d'induction d'instruction, l'évaluation contrefactuelle et les invites de production, démontrant que PE2 obtient de solides performances sur diverses tâches linguistiques. Notamment, lors de l’utilisation de l’initialisation inductive, PE2 surpasse l’APO dans 11 tâches contrefactuelles sur 12 (illustré dans la figure 6), démontrant la capacité de PE2 à raisonner sur des situations paradoxales et contrefactuelles.

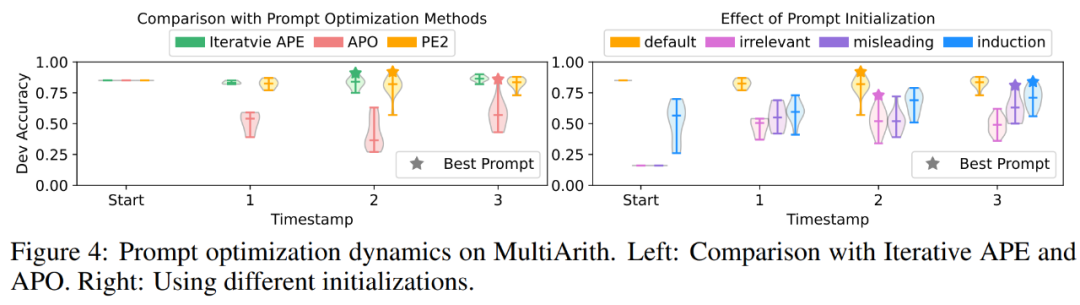
PE2 génère une édition d'invites ciblée et des invites de haute qualité. Dans la figure 4 (a), les auteurs tracent la qualité des propositions de repères au cours du processus d'optimisation des repères. Une tendance très claire a été observée dans les trois méthodes d'optimisation des signaux dans les expériences : l'APE itérative est basée sur la paraphrase, de sorte que les signaux nouvellement générés ont une variance plus petite. APO subit une modification drastique des invites, de sorte que les performances chutent dès la première étape. PE2 est la plus stable des trois méthodes. Dans le tableau 3, les auteurs répertorient les meilleurs conseils trouvés par ces méthodes. APO et PE2 peuvent fournir des instructions « examiner toutes les pièces/détails ». De plus, PE2 est conçu pour revérifier les lots, ce qui lui permet d'aller au-delà des simples modifications de paraphrase jusqu'à des modifications d'invite très spécifiques telles que « n'oubliez pas d'ajouter ou de soustraire si nécessaire ».

Pour plus d'informations, veuillez vous référer au document original.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!