Brisez la barrière de l'information ! Un outil de visualisation 3D à grande échelle choquant est sorti !

Récemment, un Néo-Zélandais, Brendan Bycroft, a créé un engouement dans le cercle technologique. Un projet qu'il a créé, appelé Large Model 3D Visualization, est non seulement en tête de liste de Hacker News, mais son effet choquant est encore plus époustouflant. Grâce à ce projet, vous comprendrez parfaitement comment fonctionne le LLM (Large Language Model) en quelques secondes seulement.

Que vous soyez passionné de technologie ou non, ce projet vous apportera un festin visuel et un éclairage cognitif sans précédent. Explorons ensemble cette superbe création !

Introduction

Dans ce projet, Bycroft a analysé en détail un modèle GPT léger appelé Nano-GPT développé par le scientifique OpenAI Andrej Karpathy. En tant que version réduite du modèle GPT, le modèle ne comporte que 85 000 paramètres. Bien entendu, bien que ce modèle soit beaucoup plus petit que le GPT-3 ou le GPT-4 d'OpenAI, on peut dire qu'« un moineau est petit mais possède tous les organes internes ».

Nano-GPT GitHub : https://github.com/karpathy/nanoGPT

Afin de faciliter la démonstration de chaque couche du modèle Transformer, Bycroft a organisé une tâche cible très simple pour le modèle Nano-GPT : le modèle l'entrée est de 6 lettres "CBABBC", la sortie est une séquence classée par ordre alphabétique, par exemple, la sortie "ABBBCC".

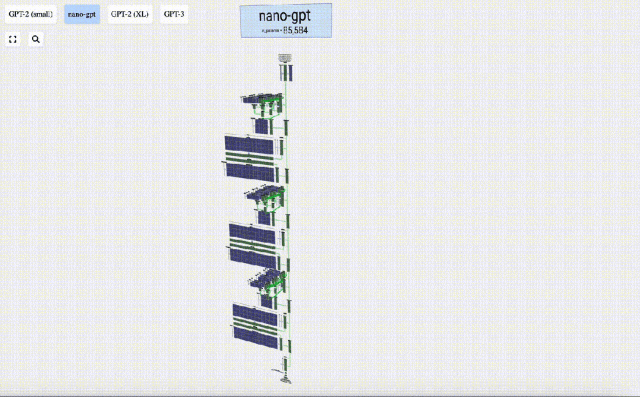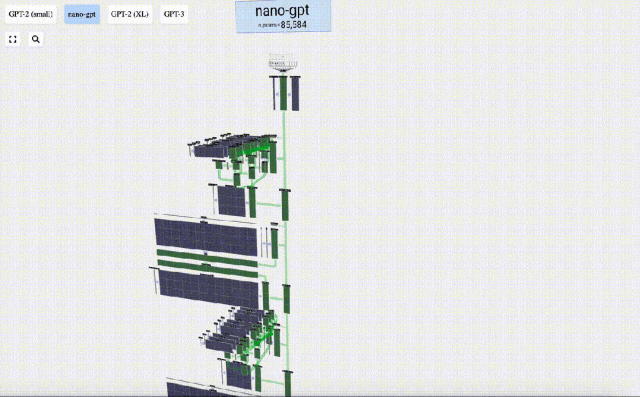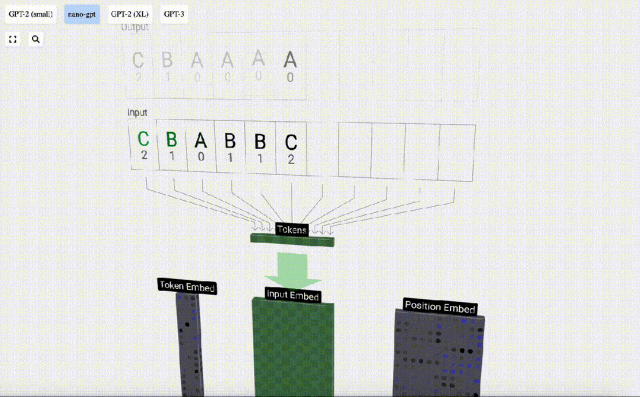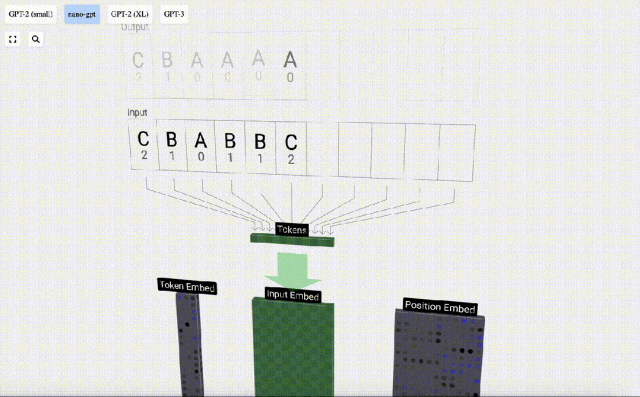
Nous appelons chaque lettre un jeton, et ces différentes lettres constituent le vocabulaire du vocabulaire :

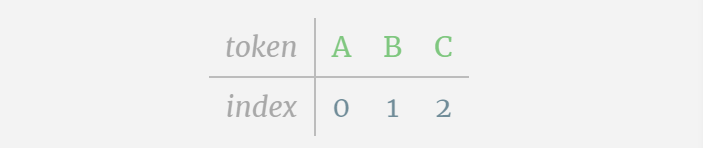
Pour cela Pour un tableau, chaque lettre se voit attribuer un index de jeton d'indice. La séquence composée de ces indices peut être utilisée comme entrée du modèle : 2 1 0 1 1 2

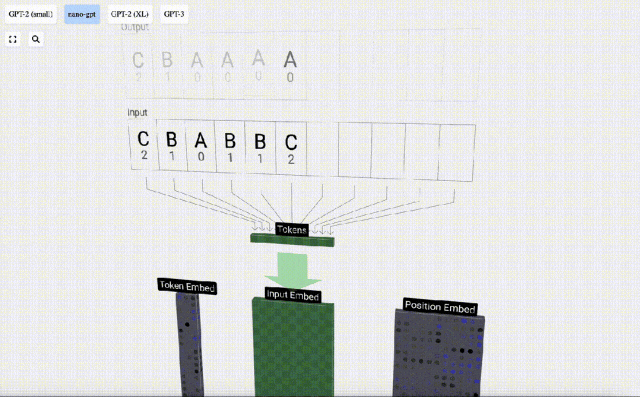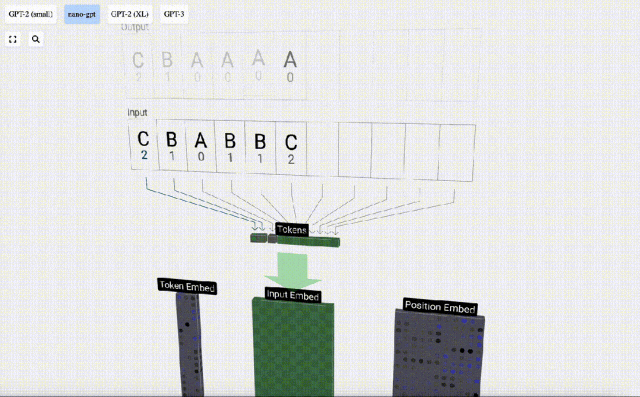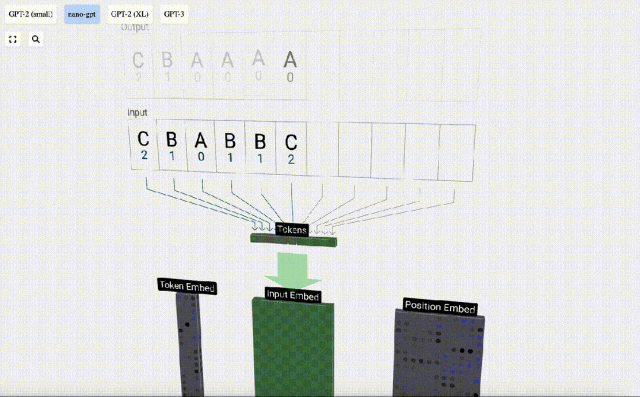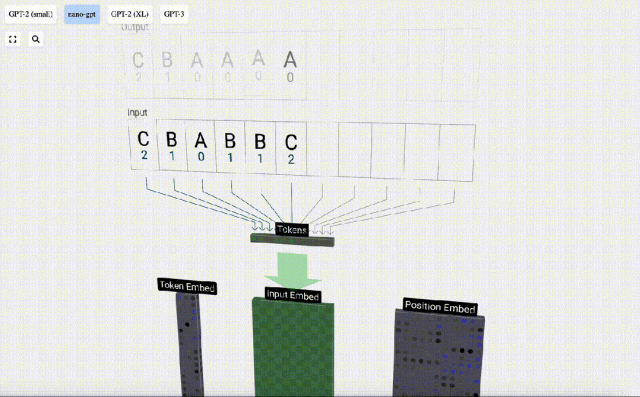
Dans la visualisation 3D, chaque cellule verte représente un nombre calculé, tandis que chaque cellule bleue représente le poids du modèle .

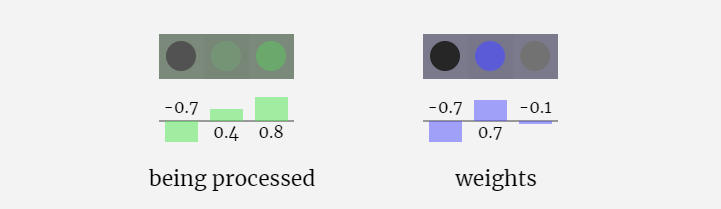
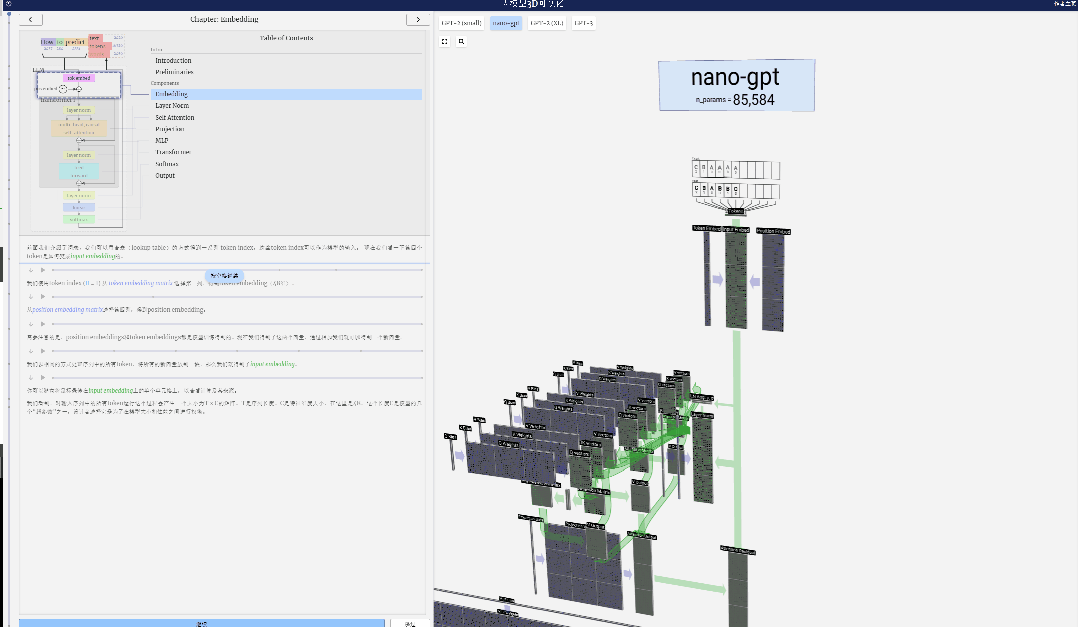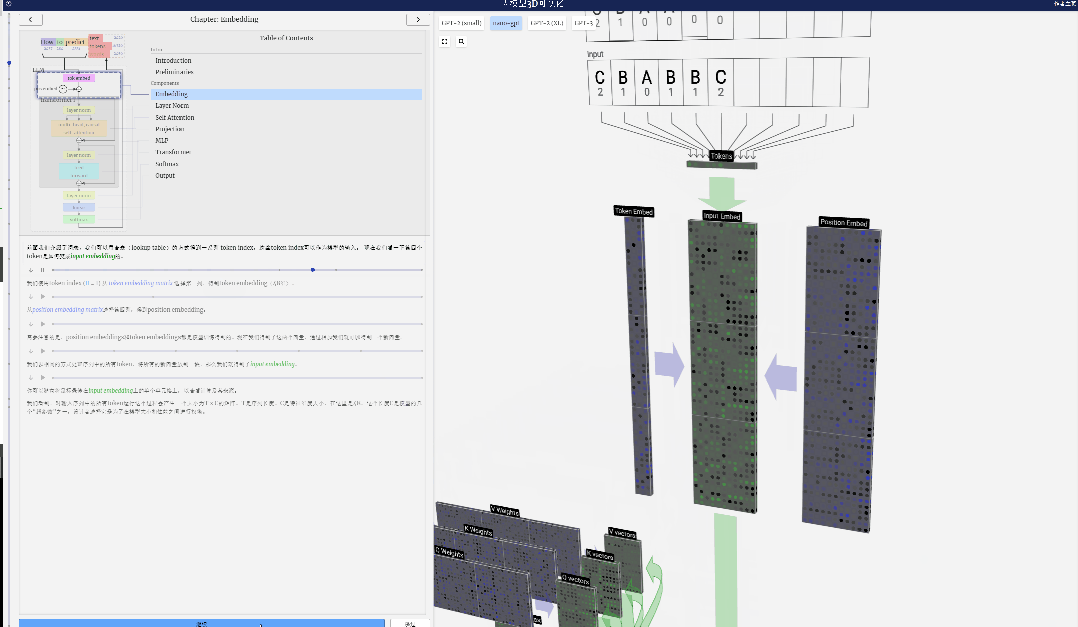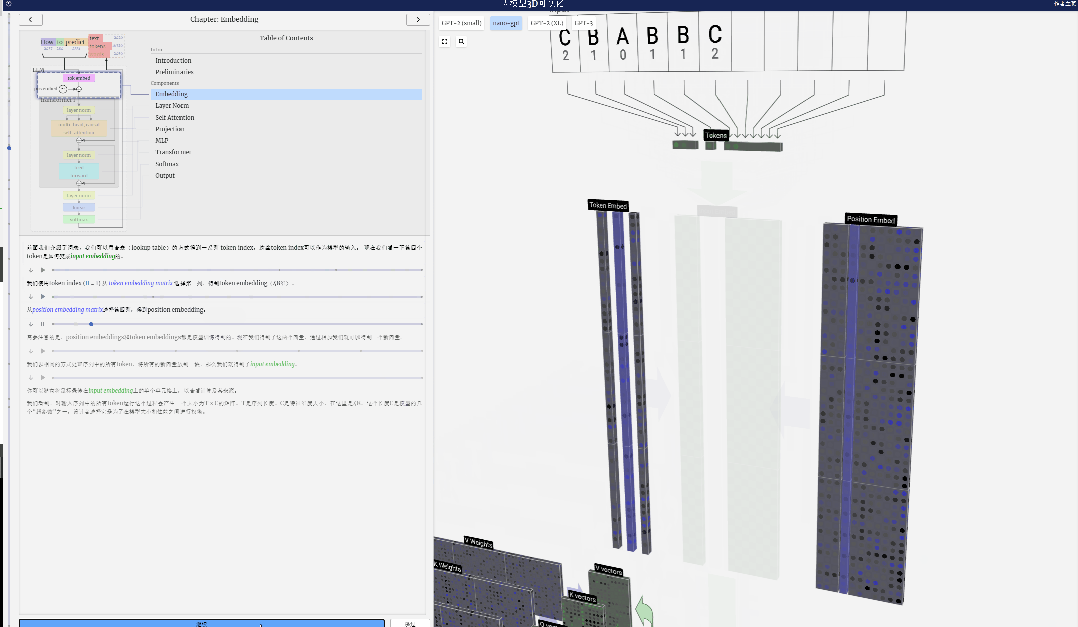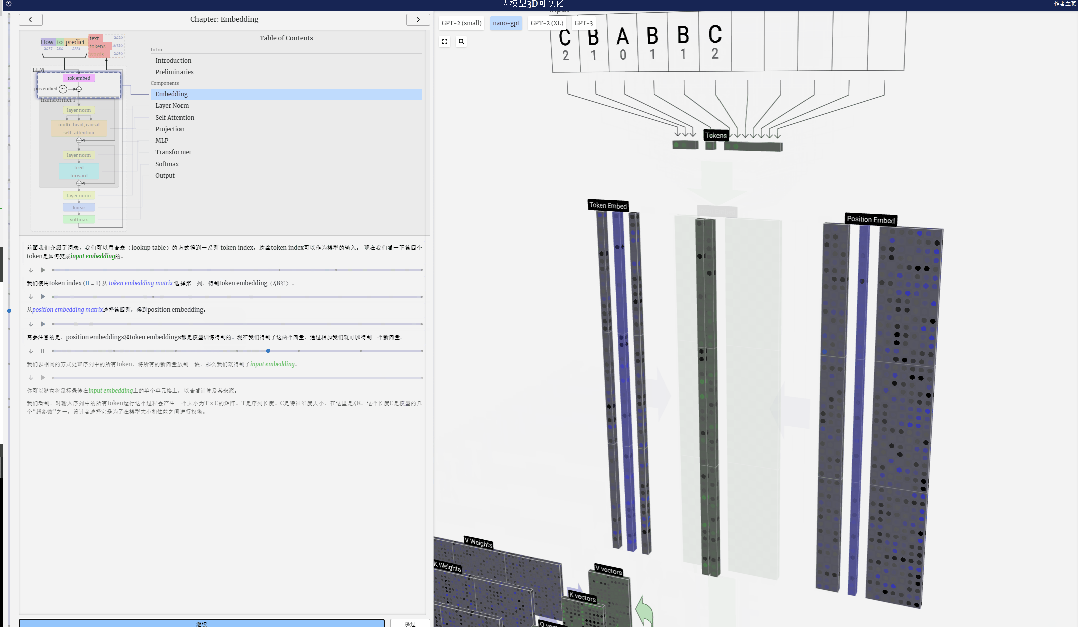
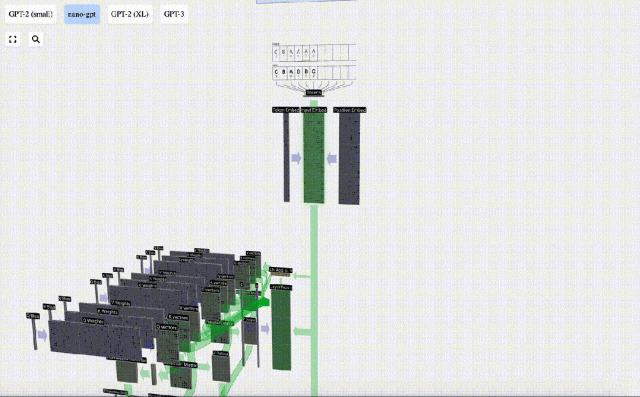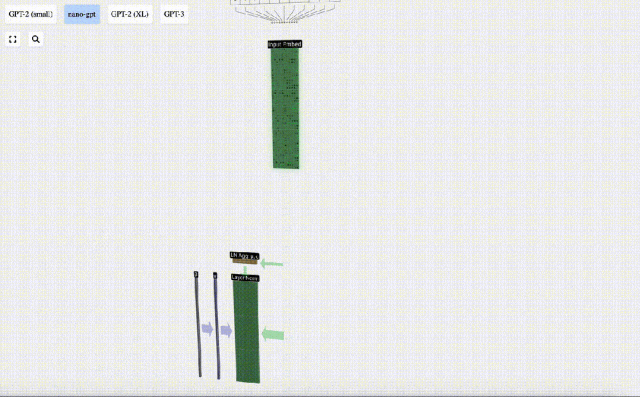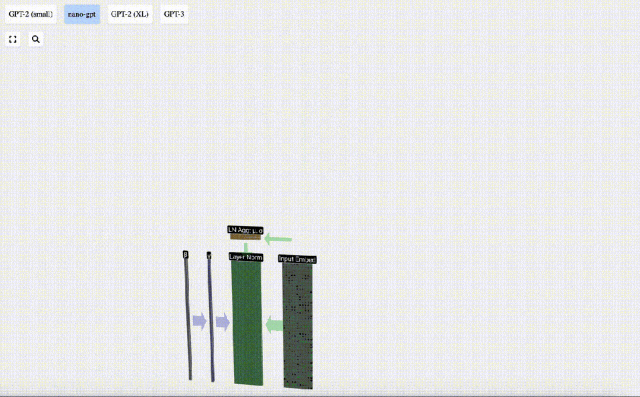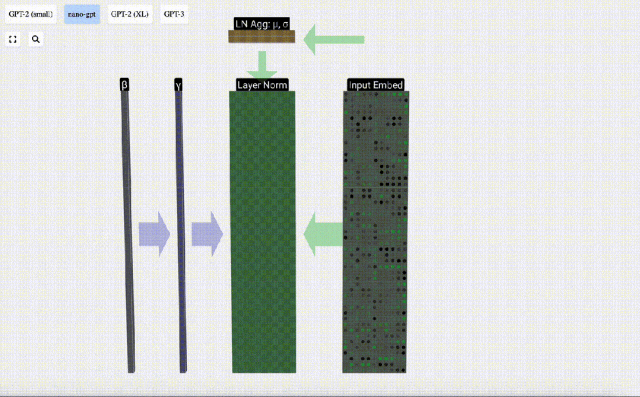
Dans le traitement de séquence, chaque nombre est d'abord converti en un vecteur de dimension C. Ce processus est appelé intégration. Dans Nano-GPT, la dimension de cette intégration est généralement de 48 dimensions. Grâce à cette opération d'intégration, chaque nombre est représenté sous forme de vecteur dans un espace à dimensions C, ce qui permet un meilleur traitement et analyse ultérieurs.

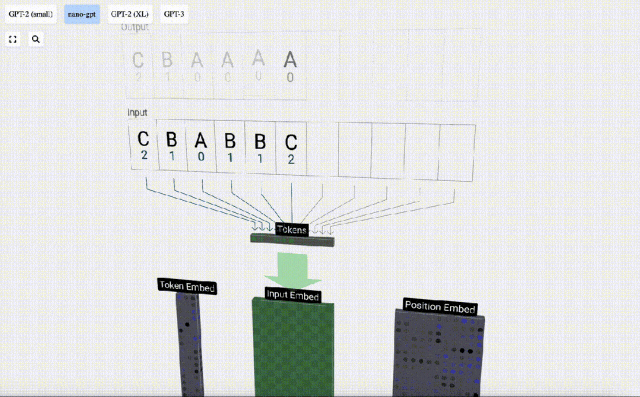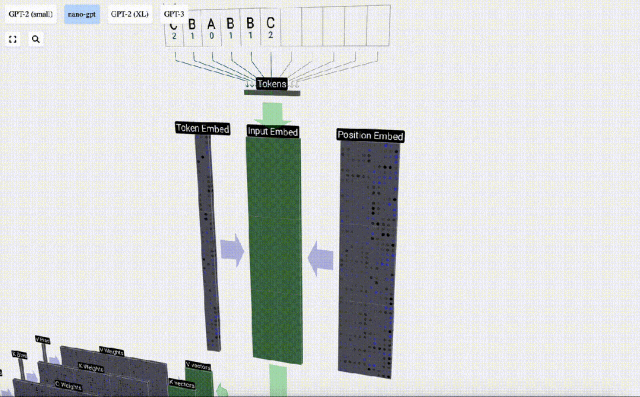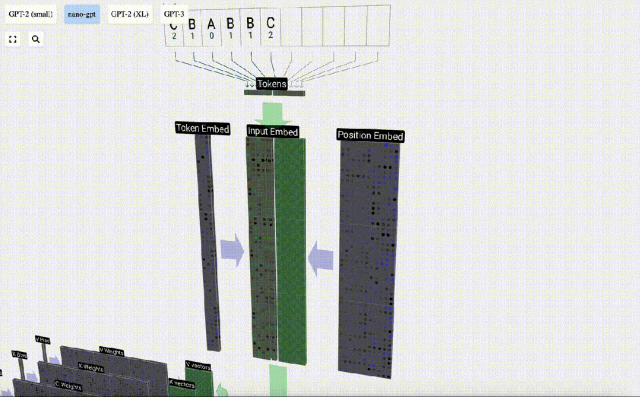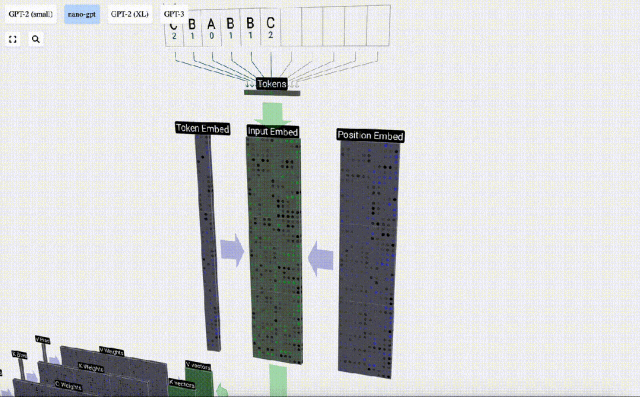
l'intégration est calculée à travers une série de couches de modèle intermédiaires, généralement appelées Transformers, et atteint finalement la couche inférieure.

"Alors, quelle est la sortie ?"

La sortie du modèle est le jeton suivant de la séquence. Donc à la fin, nous obtenons la valeur de probabilité que le prochain jeton soit A B C.

Dans cet exemple, le modèle de 6ème position génère A avec une forte probabilité. Nous pouvons maintenant transmettre A comme entrée au modèle et répéter tout le processus.

Les visualisations GPT-2 et GPT-3 sont également affichées.

• GPT-3 possède 175 milliards de paramètres et la couche modèle comporte 8 colonnes, couvrant densément tout l'écran.

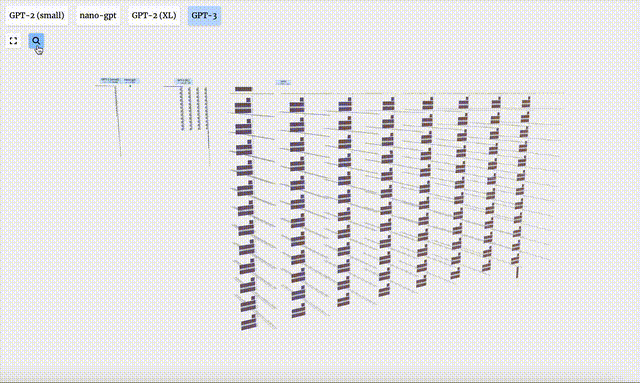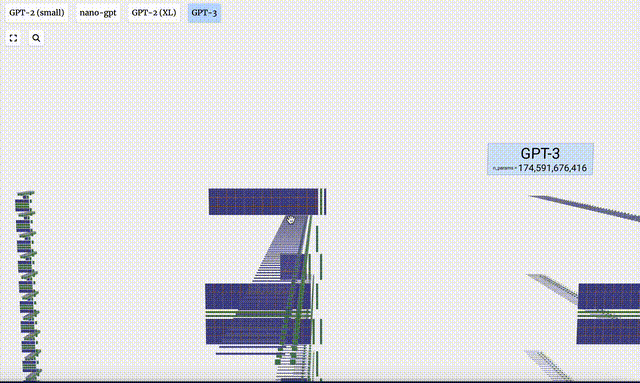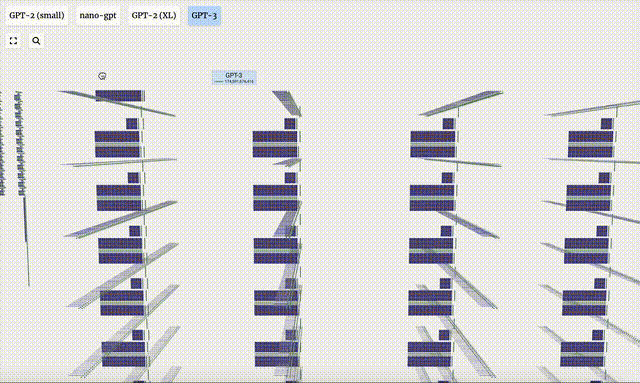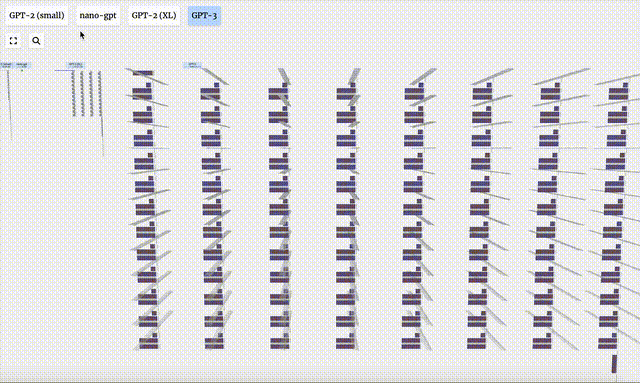
• Différentes versions de paramètres du modèle GPT-2 montrent d'énormes différences architecturales. Nous prenons ici comme exemples les 15 milliards de paramètres de GPT-2 (XL) et les 124 millions de paramètres de GPT-2 (Small).

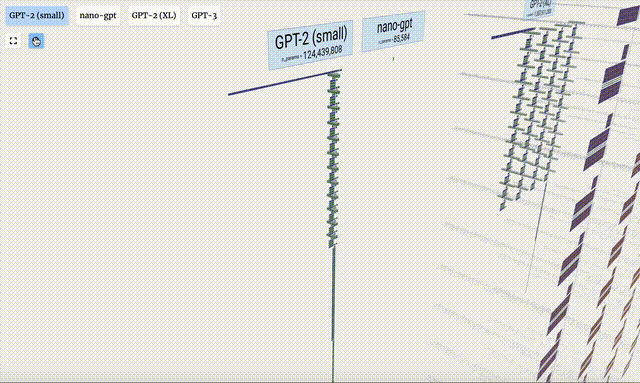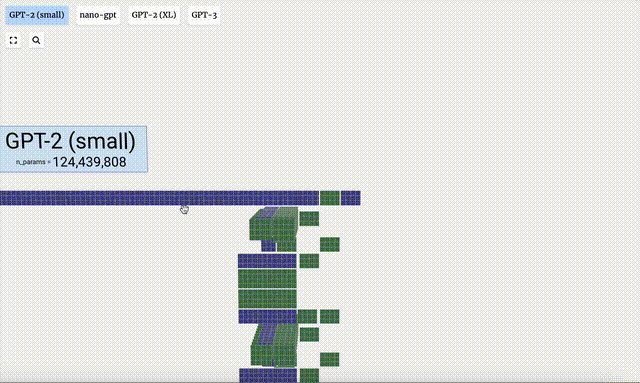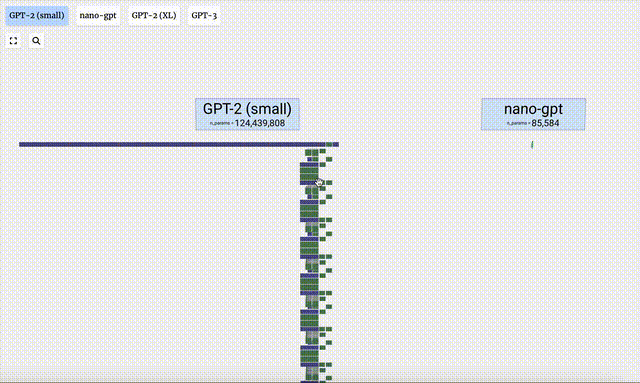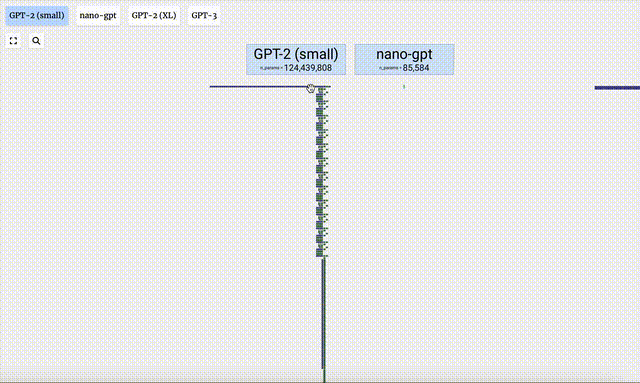
Il convient de noter que cette visualisation se concentre principalement sur l'inférence de modèle (inférence), et non sur la formation, ce n'est donc qu'une petite partie de l'ensemble du processus d'apprentissage automatique. De plus, on suppose ici que les poids du modèle ont été pré-entraînés, puis l'inférence du modèle est utilisée pour générer la sortie.

Intégration

Comme mentionné précédemment, comment utiliser une simple table de recherche pour mapper des jetons à une série d'entiers.

Ces entiers, l'index symbolique, sont la première et la seule fois où nous voyons des entiers dans le modèle. Après cela, les opérations seront effectuées à l'aide de nombres à virgule flottante (nombres décimaux).

Ici, prenons le 4ème jeton (index 3) comme exemple pour voir comment il est utilisé pour générer le 4ème vecteur colonne de l'intégration d'entrée.

Utilisez d'abord l'index de jeton (ici, prenez B=1 comme exemple) pour sélectionner la deuxième colonne de la matrice d'incorporation de jetons et obtenez un vecteur de colonne de taille C=48 (48 dimensions), appelé intégration de jetons. .

Sélectionnez ensuite la quatrième colonne de la matrice d'intégration de position ("Parce qu'ici nous regardons principalement le (t = 3) jeton B à la 4ème position"), de même, nous obtenons une taille de C=48 (48 dimensions) Vecteur de colonne, appelé intégration de position.

Il convient de noter que les intégrations de positions et les intégrations de jetons sont toutes deux obtenues par formation de modèle (indiquées en bleu). Maintenant que nous avons ces deux vecteurs, en les additionnant nous pouvons obtenir un nouveau vecteur colonne de taille C=48.

Ensuite, traitez tous les jetons de la séquence dans le même processus, en créant un ensemble de vecteurs contenant les valeurs des jetons et leurs positions.

Comme le montre la figure ci-dessus, l'exécution de ce processus sur tous les jetons de la séquence d'entrée produira une matrice de taille TxC. Parmi eux, T représente la longueur de la séquence. C signifie canal, mais est également appelé fonctionnalité ou dimension ou taille d'intégration, qui dans ce cas est 48. Cette longueur C est l'un des nombreux « hyperparamètres » du modèle, choisis par le concepteur pour fournir un compromis entre la taille du modèle et les performances.

Cette matrice de dimension TxC est l'intégration d'entrée et est transmise à travers le modèle.

Petite Astuce : N'hésitez pas à passer votre souris sur une seule cellule de l'intégration d'entrée pour voir le calcul et sa source.

Norme de couche

La matrice d'intégration d'entrée obtenue précédemment est l'entrée de la couche Transformer.

La première étape de la couche Transformer consiste à effectuer une normalisation de couche sur la matrice d'intégration d'entrée. Il s'agit d'une opération permettant de normaliser les valeurs de chaque colonne de la matrice d'entrée.

La normalisation est une étape importante dans la formation approfondie des réseaux neuronaux, qui contribue à améliorer la stabilité du modèle pendant le processus de formation.

Nous pouvons regarder les colonnes de la matrice séparément. La quatrième colonne est prise comme exemple ci-dessous.

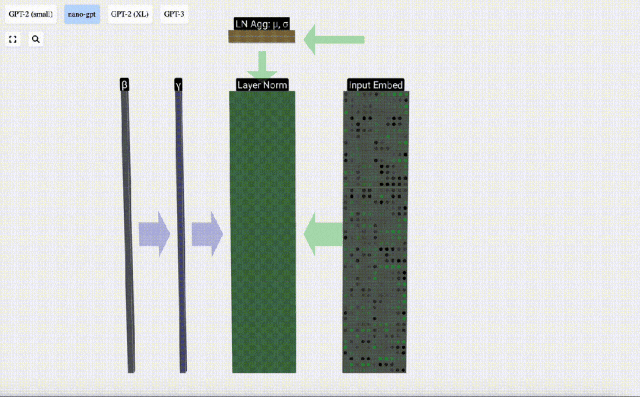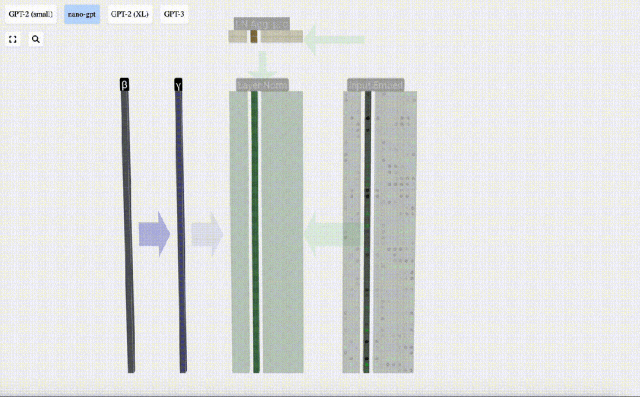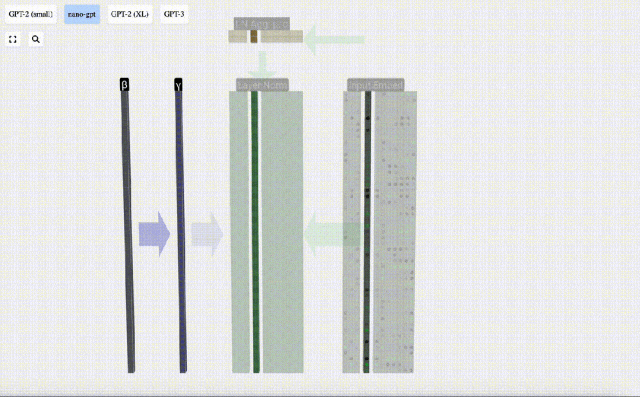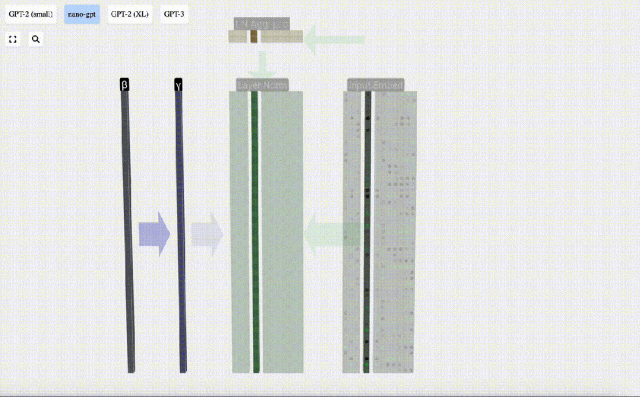
Le but de la normalisation est de faire en sorte que la valeur de chaque colonne ait une moyenne de 0 et un écart type de 1. Pour y parvenir, calculez la moyenne et l’écart type de chaque colonne, puis soustrayez la moyenne correspondante et divisez par l’écart type correspondant pour chaque colonne.

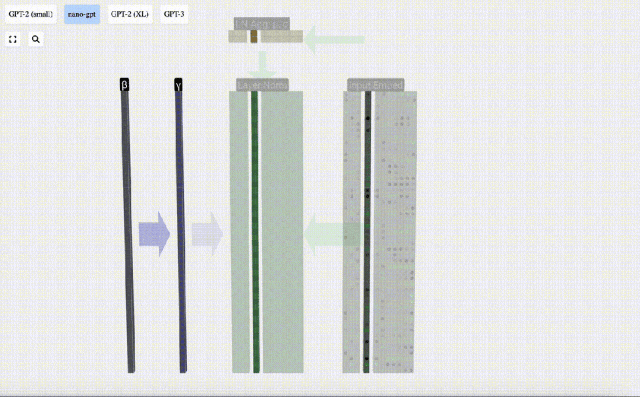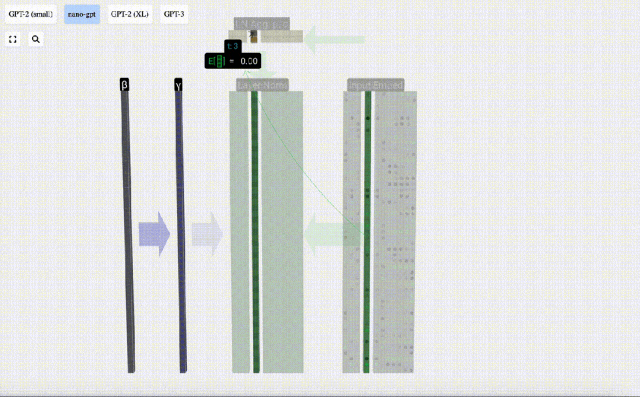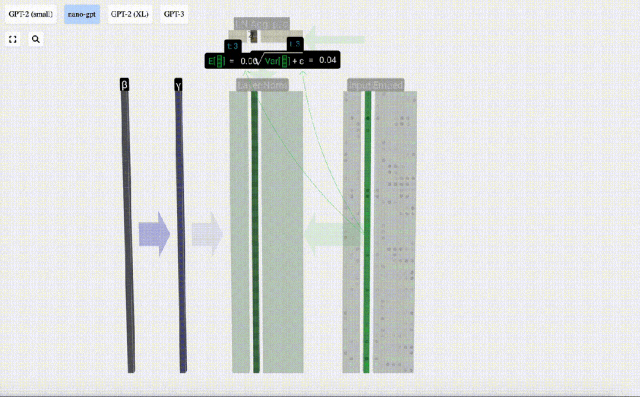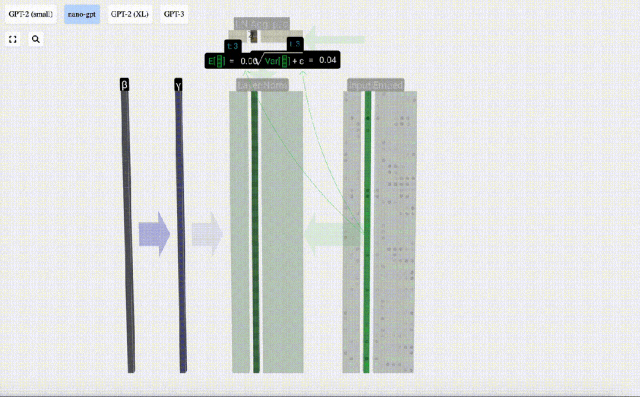
Ici, E[x] est utilisé pour représenter la moyenne, et Var[x] est utilisé pour représenter la variance (le carré de l'écart type). epsilon(ε = 1×10^-5) sert à empêcher les erreurs de division par 0.

Calculez et stockez le résultat normalisé, puis multipliez-le par le poids d'apprentissage (γ) et ajoutez le biais (β) pour obtenir le résultat final normalisé.

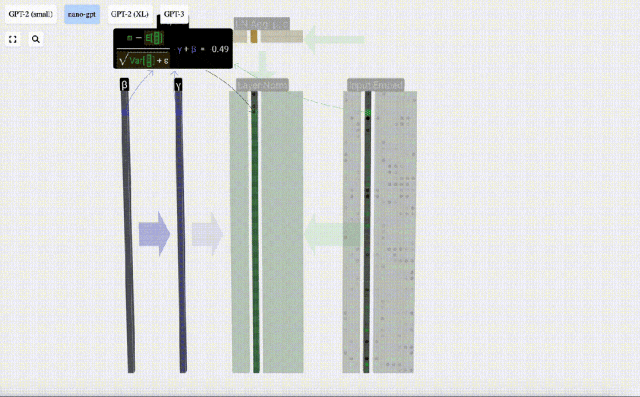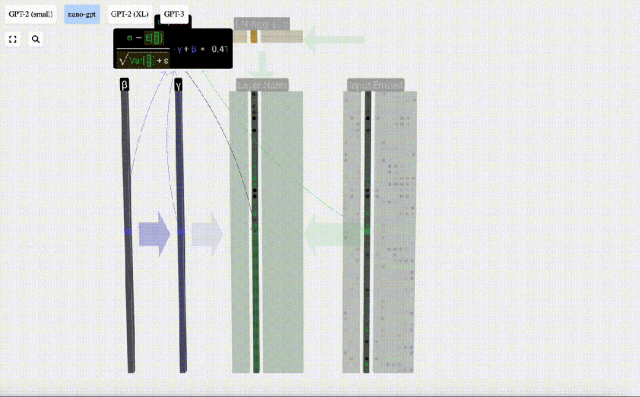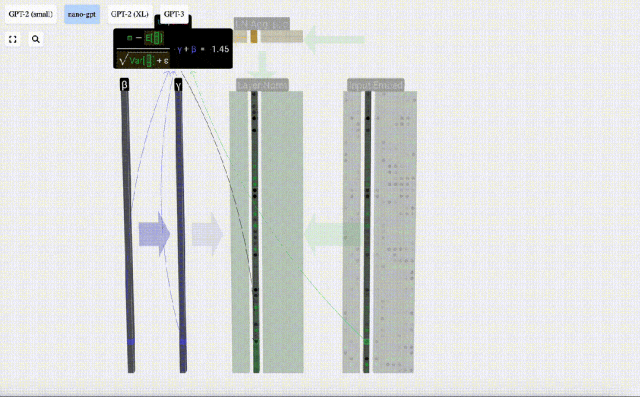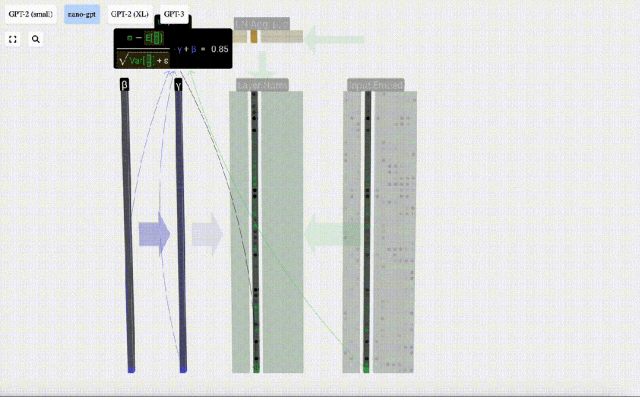
Enfin, effectuez l'opération de normalisation sur chaque colonne de la matrice d'intégration d'entrée pour obtenir l'intégration d'entrée normalisée et transmettez-la à la couche d'auto-attention (auto-attention).

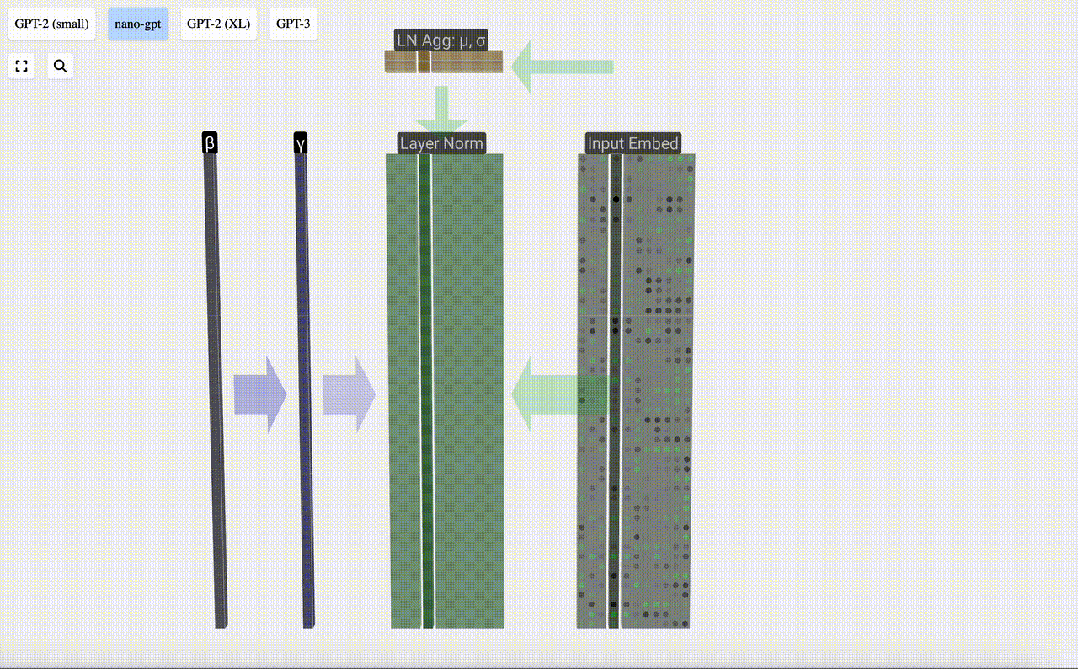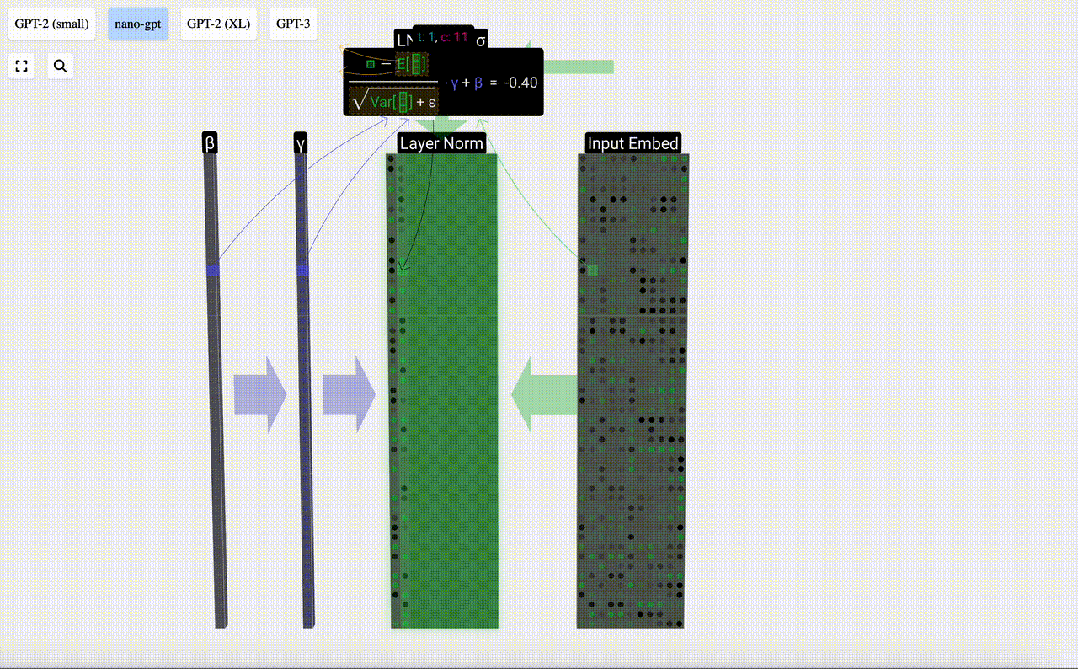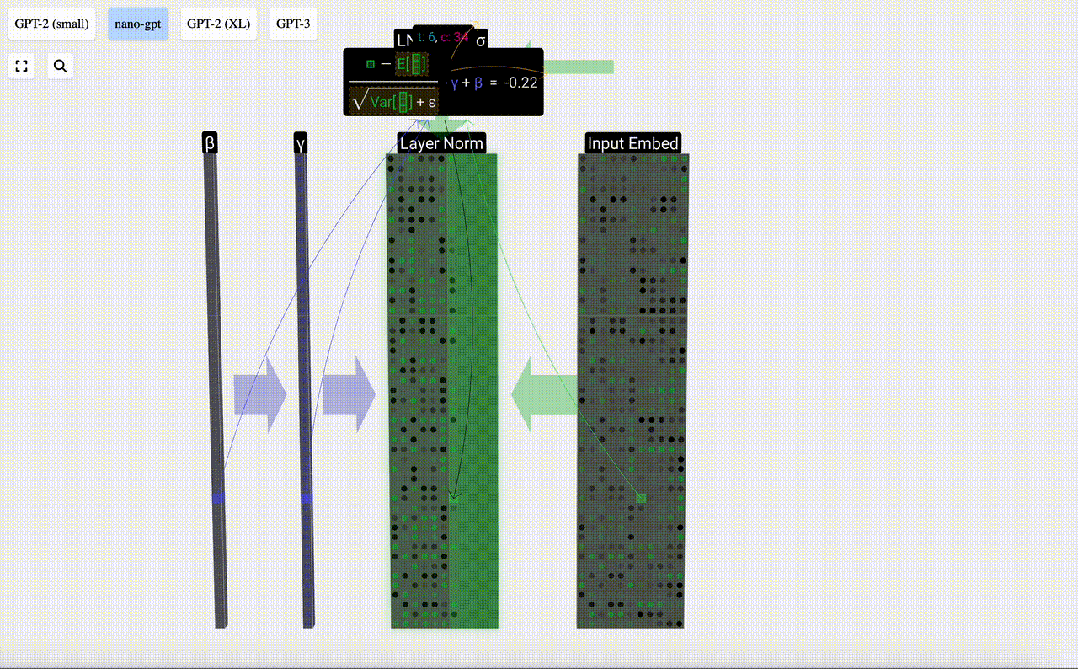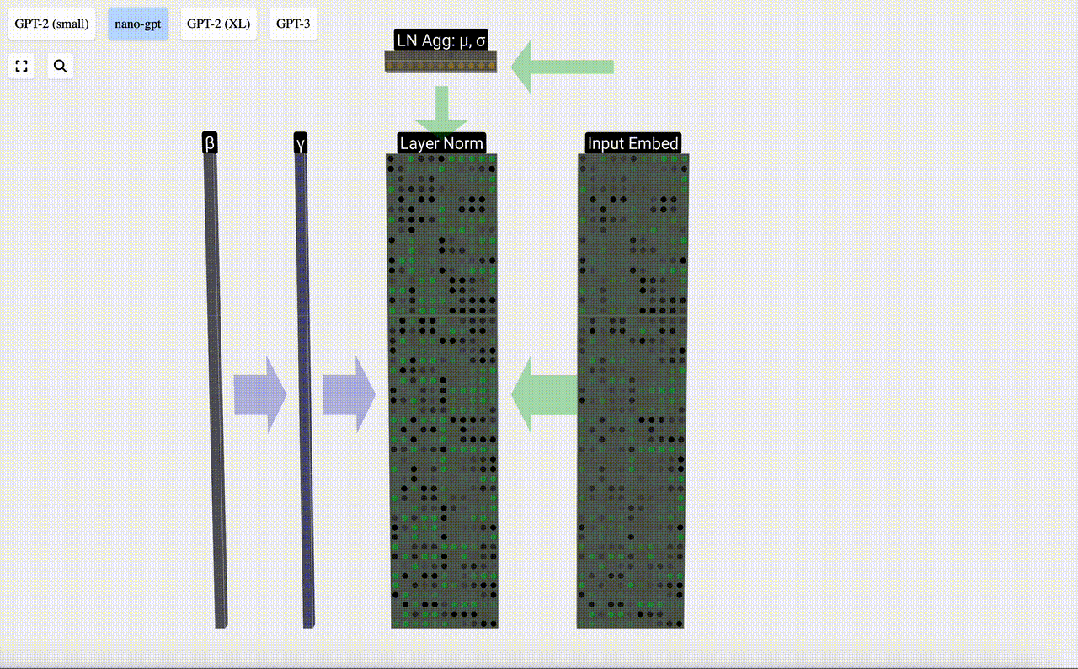
Self Attention

La couche Self Attention est probablement la partie centrale du Transformer. À ce stade, les colonnes de l'intégration d'entrée peuvent "communiquer" entre elles, tandis qu'à d'autres étapes, chaque colonne existe indépendamment.

La couche Self Attention se compose de plusieurs têtes d’auto-attention. Dans cet exemple, il y a trois têtes d’auto-attention. L'entrée de chaque en-tête représente 1/3 de l'intégration d'entrée, et nous nous concentrons uniquement sur l'un d'entre eux maintenant.

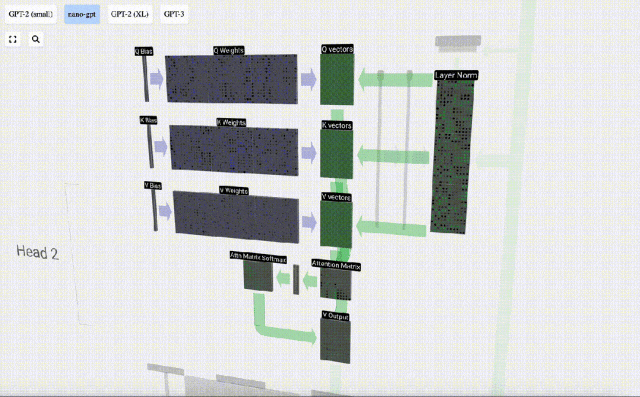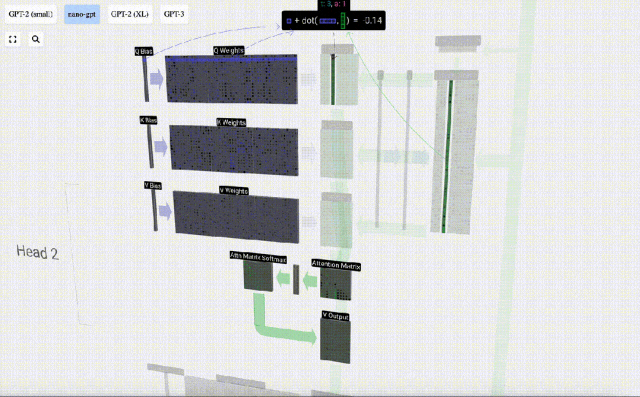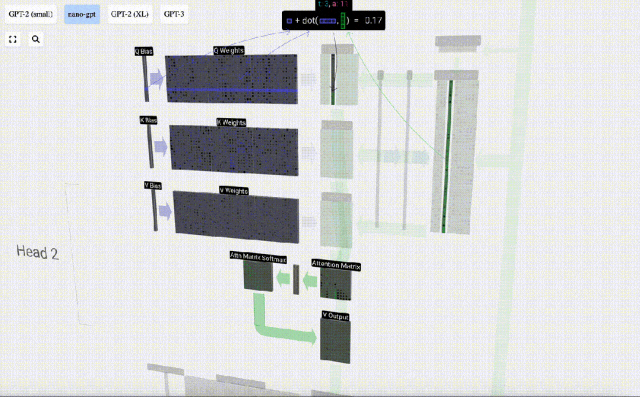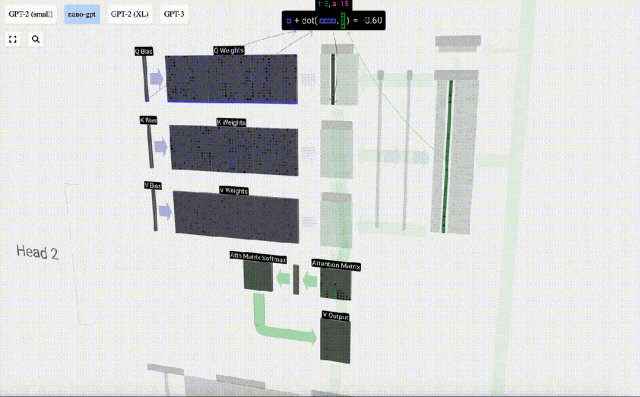
La première étape consiste à générer 3 vecteurs pour chaque colonne à partir de la colonne C de la matrice d'intégration d'entrée normalisée, qui sont QKV :

• Q : vecteur de requête
• K : vecteur clé Vecteur clé
• V : valeur vecteur Vecteur de valeur

Pour générer ces vecteurs, une multiplication matrice-vecteur est utilisée, plus un biais. Chaque unité de sortie est une combinaison linéaire de vecteurs d'entrée.

Par exemple, pour le vecteur de requête, il est complété par l'opération de produit scalaire entre une ligne de la matrice de poids Q et une colonne de la matrice d'entrée.

Le fonctionnement du produit scalaire est très simple, il suffit de multiplier les éléments correspondants puis de les ajouter.

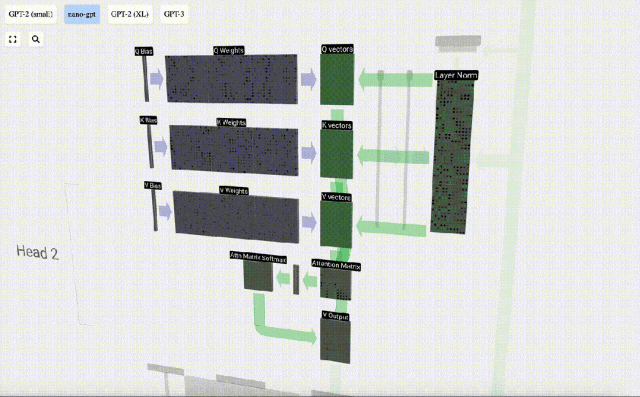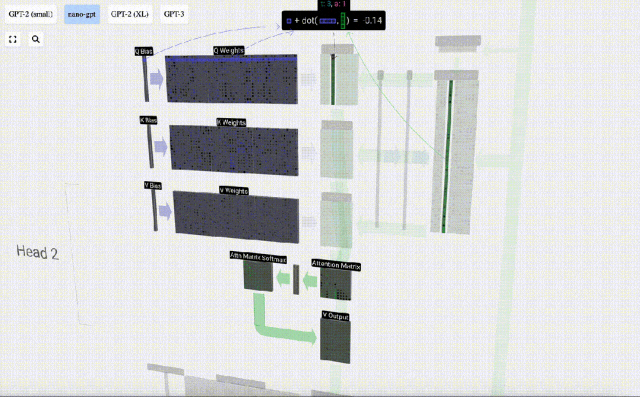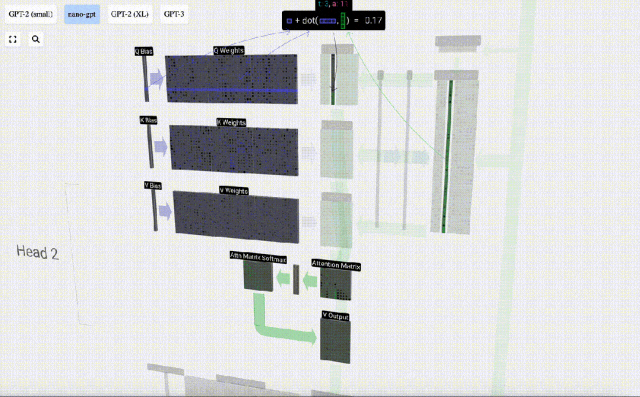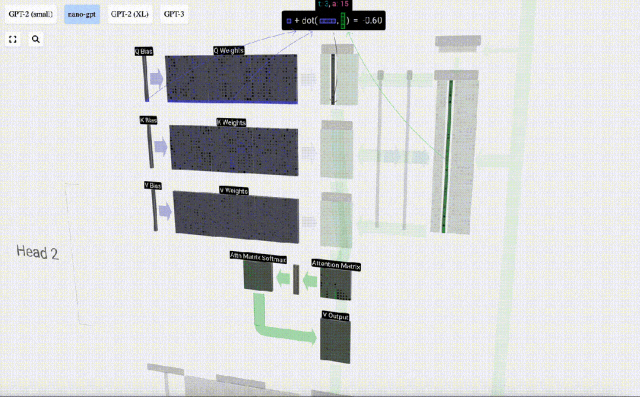
Il s'agit d'un moyen général et simple de garantir que chaque élément de sortie est affecté par tous les éléments du vecteur d'entrée (cette influence est déterminée par le poids). C’est pourquoi il apparaît souvent dans les réseaux de neurones.

Dans les réseaux de neurones, ce mécanisme se produit souvent car il permet au modèle de prendre en compte chaque partie de la séquence d'entrée lors du traitement des données. Ce mécanisme d’attention complet est au cœur de nombreuses architectures de réseaux neuronaux modernes, en particulier lors du traitement de données séquentielles telles que du texte ou des séries chronologiques.

Nous répétons cela pour chaque unité de sortie dans les vecteurs Q, K, V :

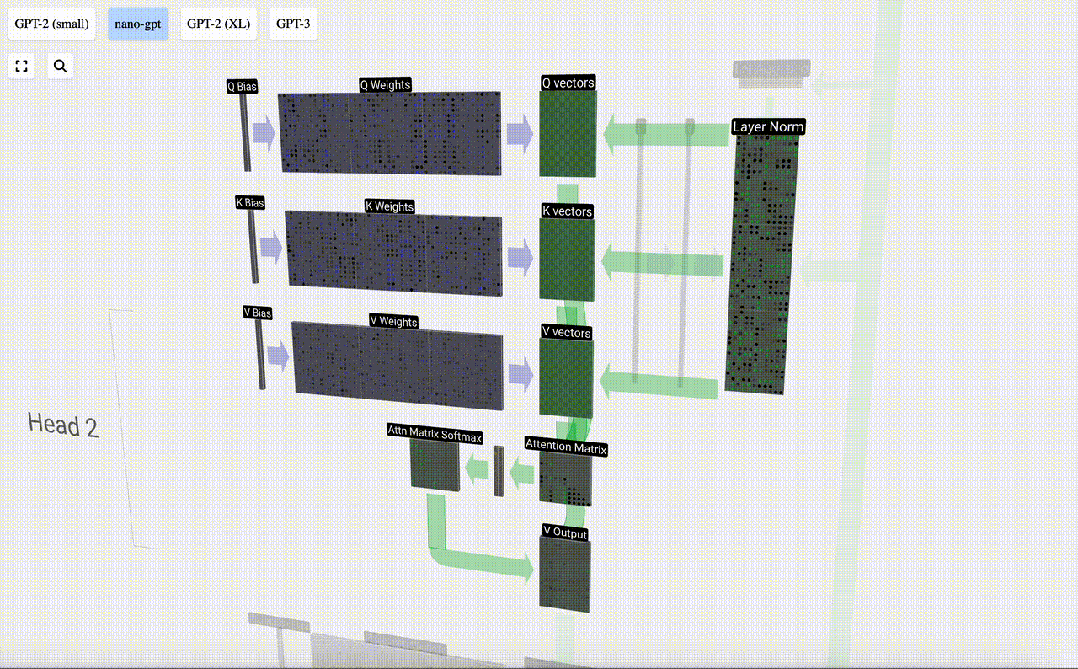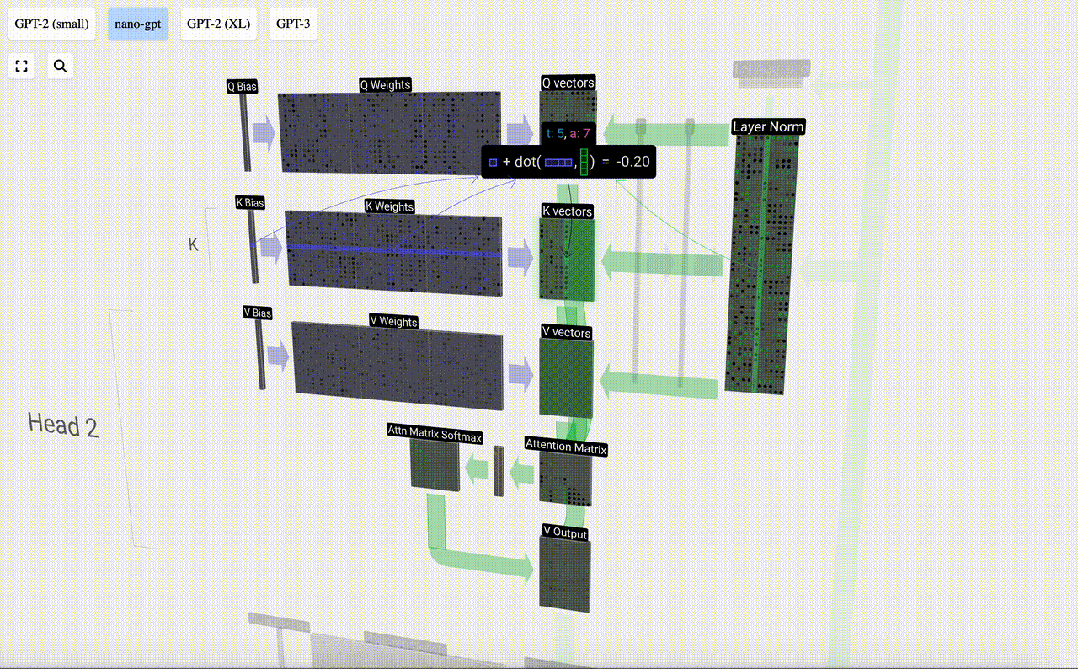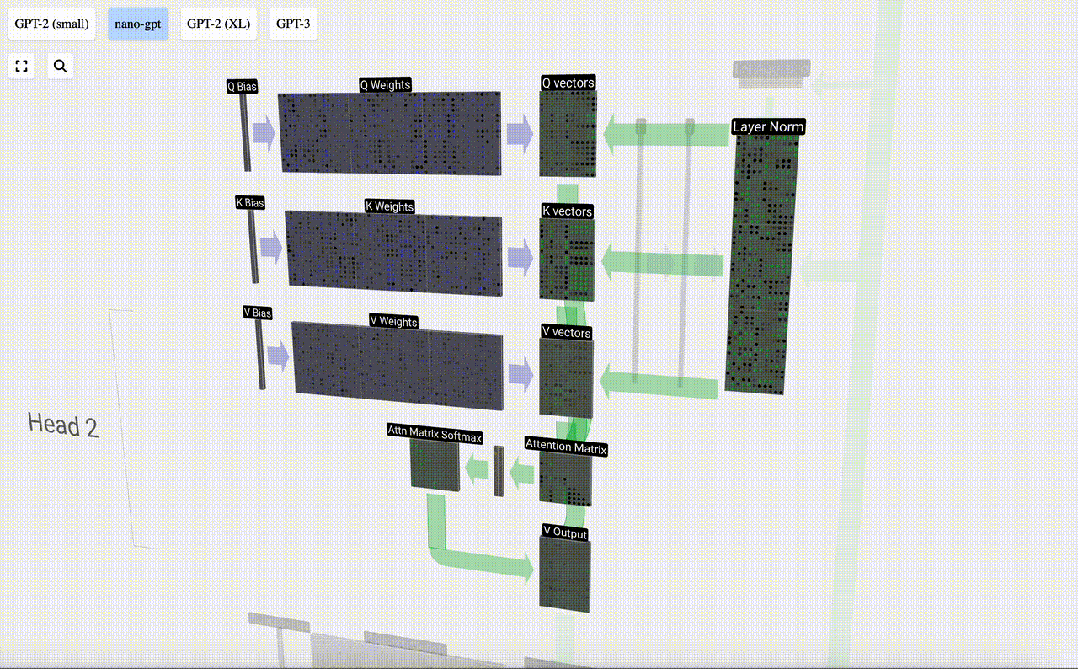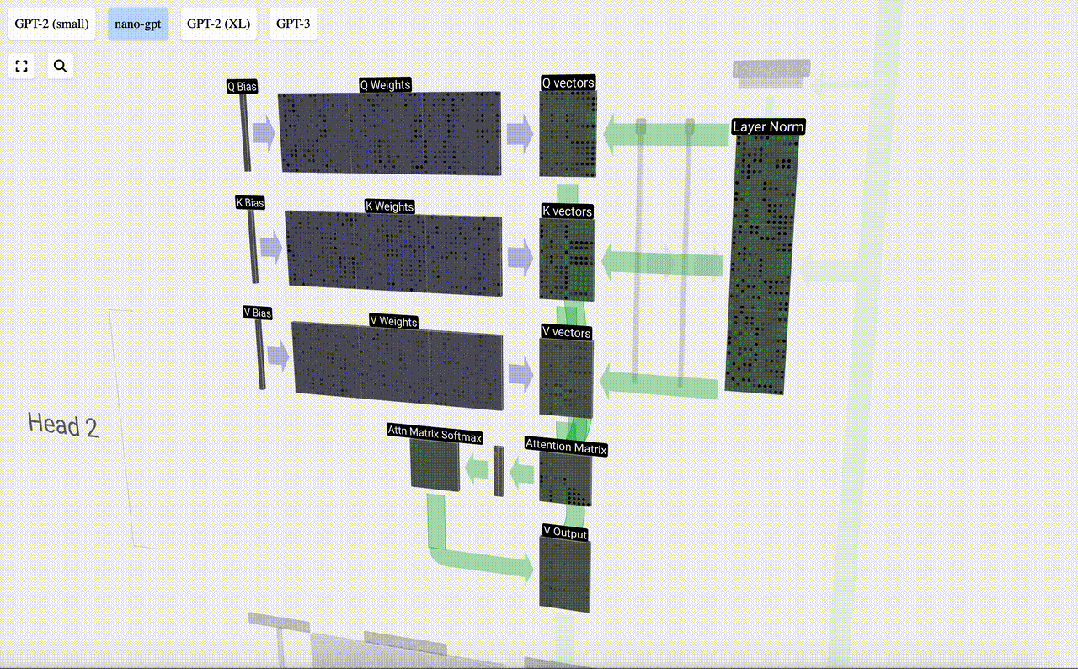
Comment utilisons-nous nos vecteurs Q (requête), K (clé) et V (valeur) ? Leur dénomination nous donne un indice : « clé » et « valeur » rappellent les types de dictionnaires, avec des clés mappées sur des valeurs. Ensuite, « requête » est ce que nous utilisons pour trouver la valeur.

Dans le cas de Self Attention, au lieu de renvoyer un seul vecteur (terme), nous renvoyons une combinaison pondérée de vecteurs (termes). Pour trouver ce poids, nous calculons le produit scalaire entre un vecteur Q et chaque vecteur K, le pondérons et le normalisons, et enfin le multiplions par le vecteur V correspondant et les additionnons.

En prenant comme exemple la 6ème colonne (t=5), la requête partira de cette colonne :

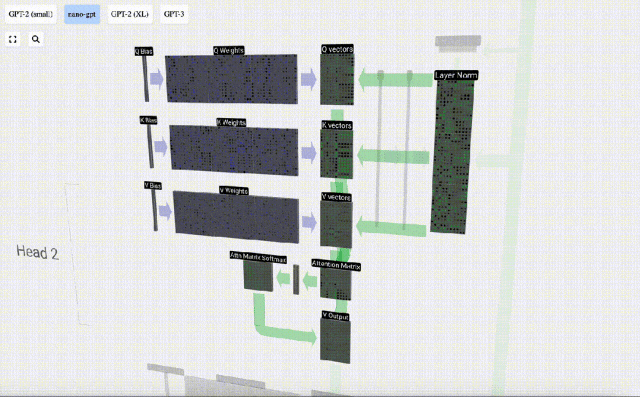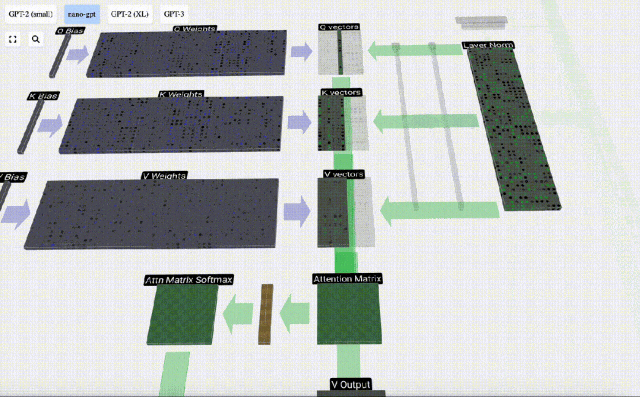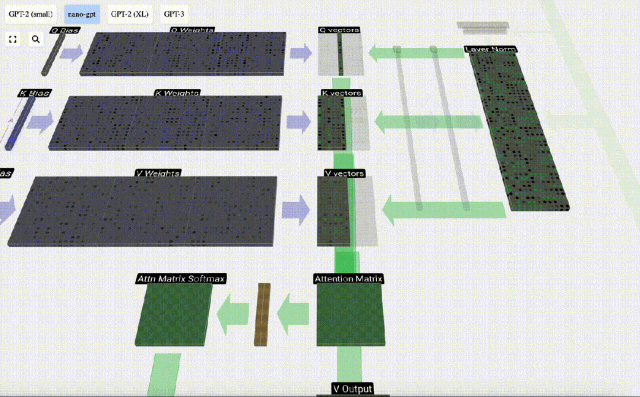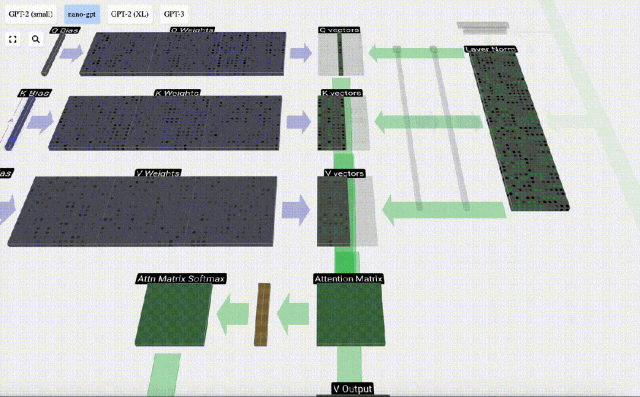
Du fait de l'existence d'une matrice d'attention, les 6 premières colonnes de KV peuvent être interrogées, et la valeur Q est l’heure actuelle.

Calculez d'abord le produit scalaire entre le vecteur Q de la colonne actuelle (t=5) et le vecteur K des colonnes précédentes (les 6 premières colonnes). Ceci est ensuite stocké dans la ligne correspondante (t=5) de la matrice d'attention.

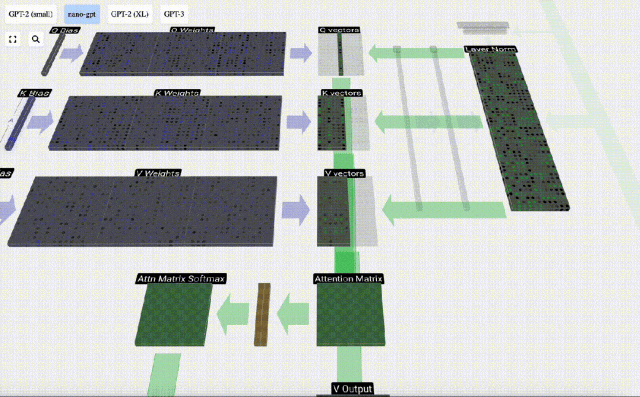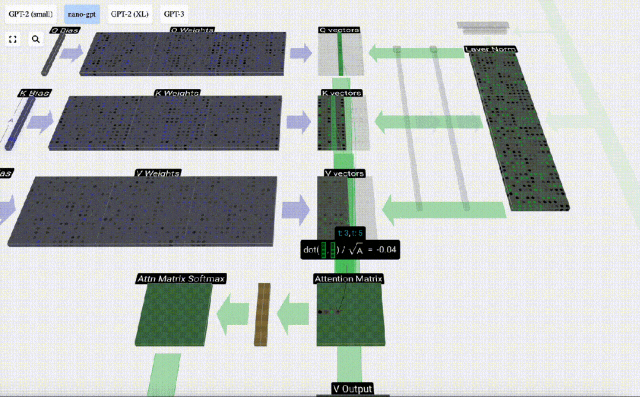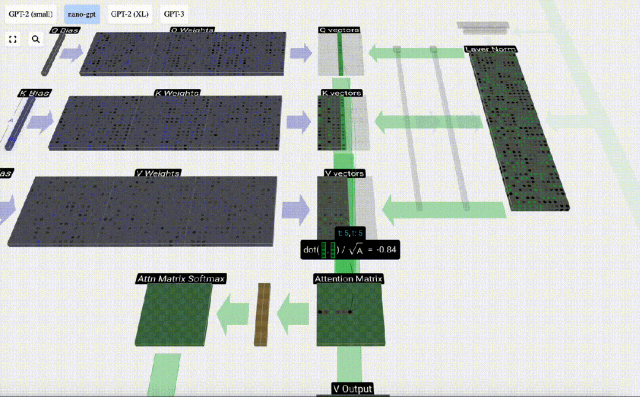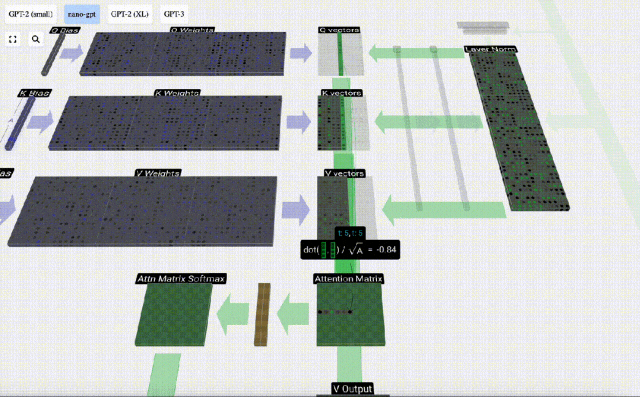
La taille du produit scalaire mesure la similarité entre deux vecteurs. Plus le produit scalaire est grand, plus ils sont similaires.

Et seul le vecteur Q fonctionne avec le vecteur K passé, ce qui en fait une auto-attention causale. En d’autres termes, les jetons ne peuvent pas « voir les informations futures ».

Ainsi, après avoir trouvé le produit scalaire, divisez par sqrt(A), où A est la longueur du vecteur QKV, cette mise à l'échelle est effectuée pour empêcher de grandes valeurs de dominer la prochaine étape de normalisation (softmax).

Ensuite, l'opération softmax est effectuée pour réduire la plage de valeurs de 0 à 1.

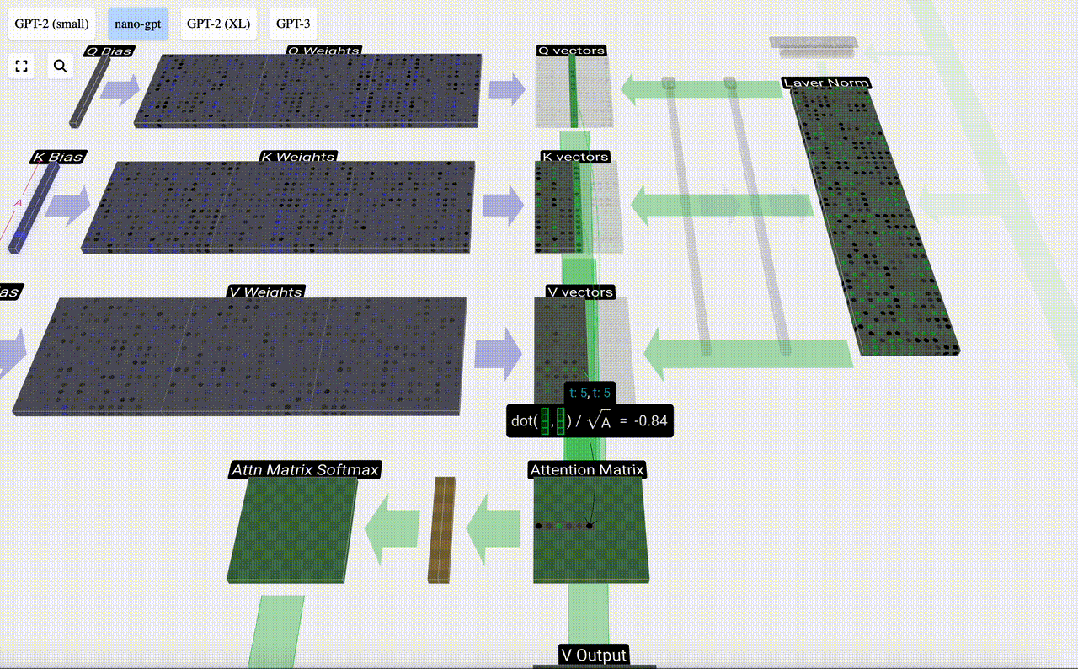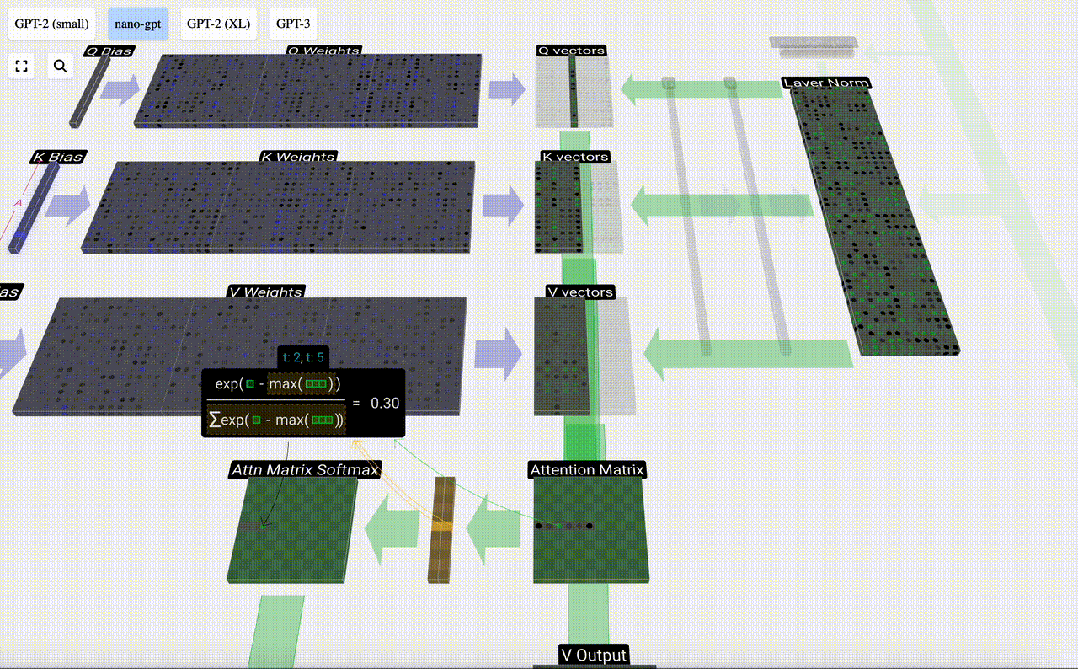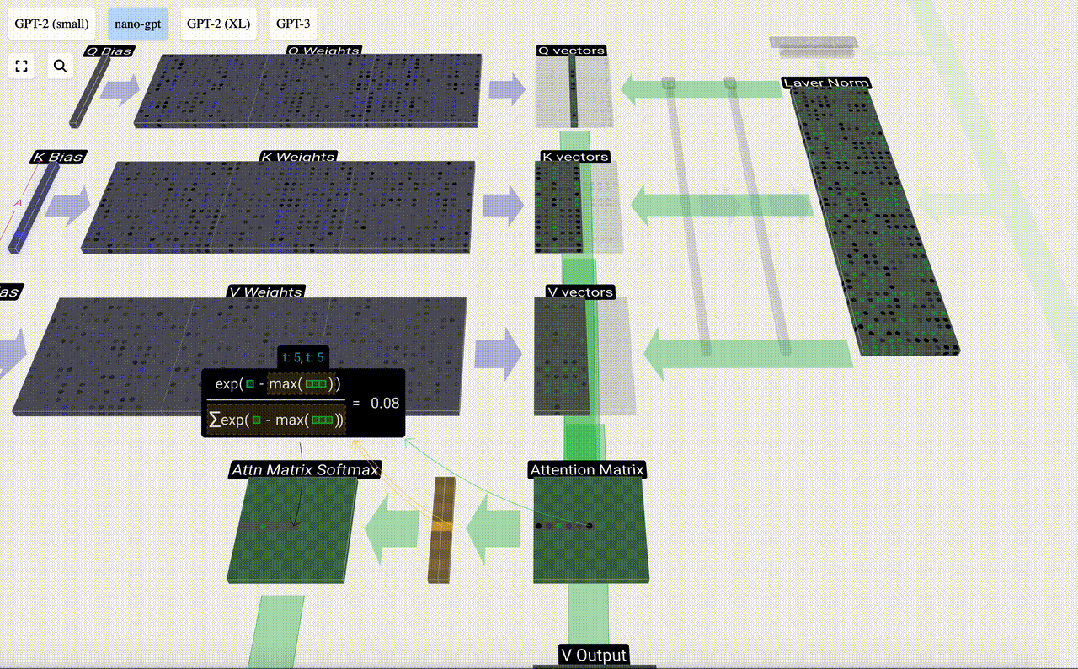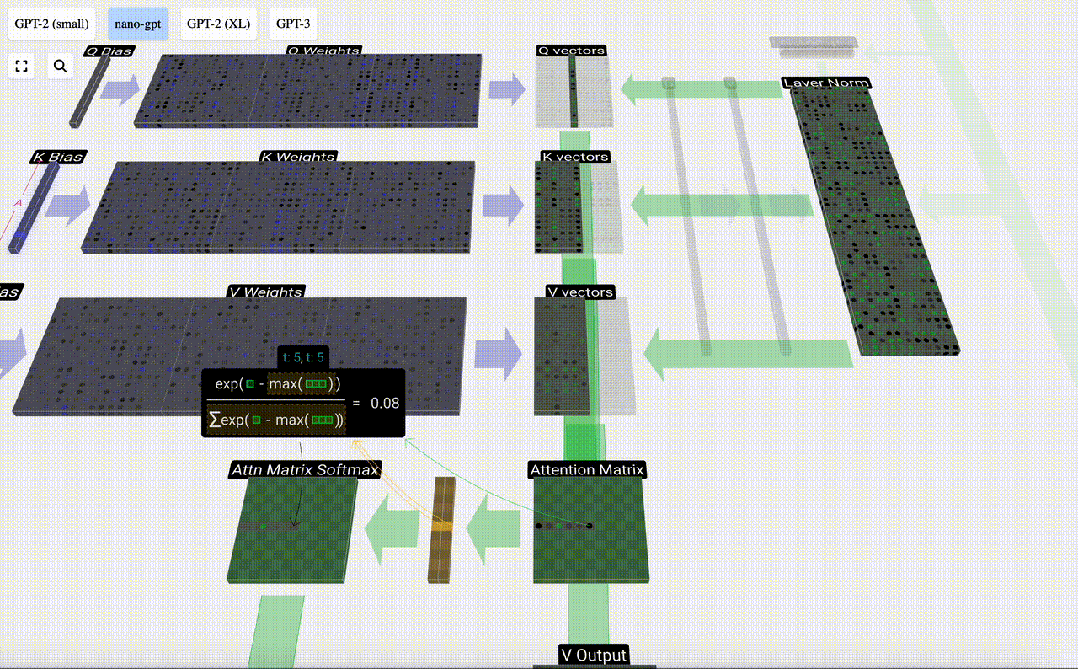
Enfin, le vecteur de sortie de cette colonne (t=5) peut être obtenu. Regardez la ligne (t=5) de la matrice d'attention normalisée et multipliez chaque élément par le vecteur V correspondant de l'autre colonne.

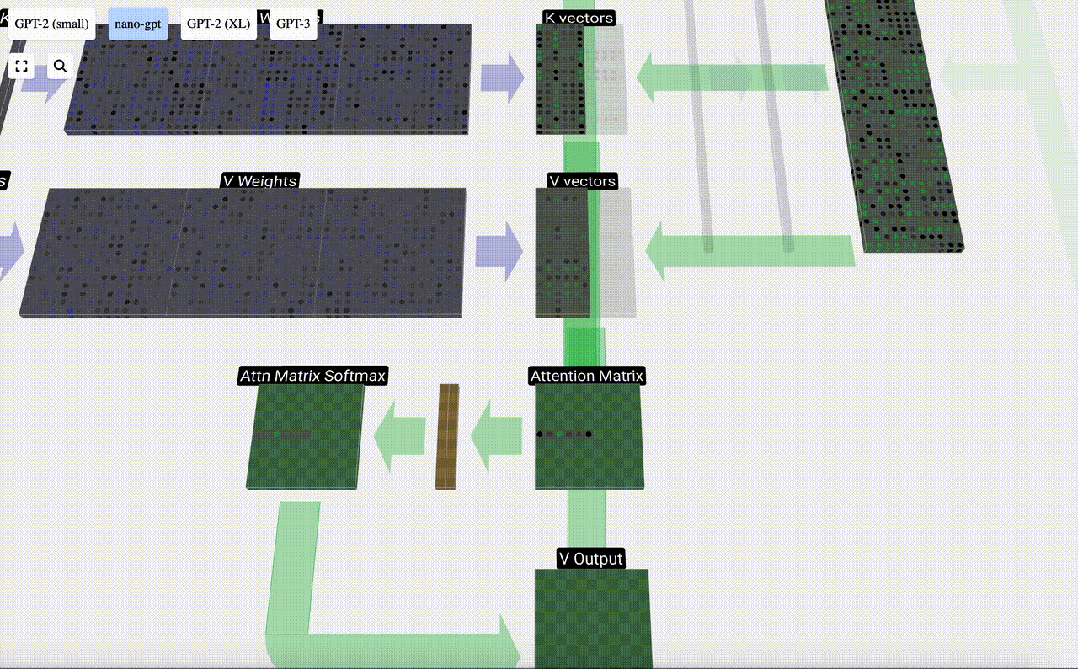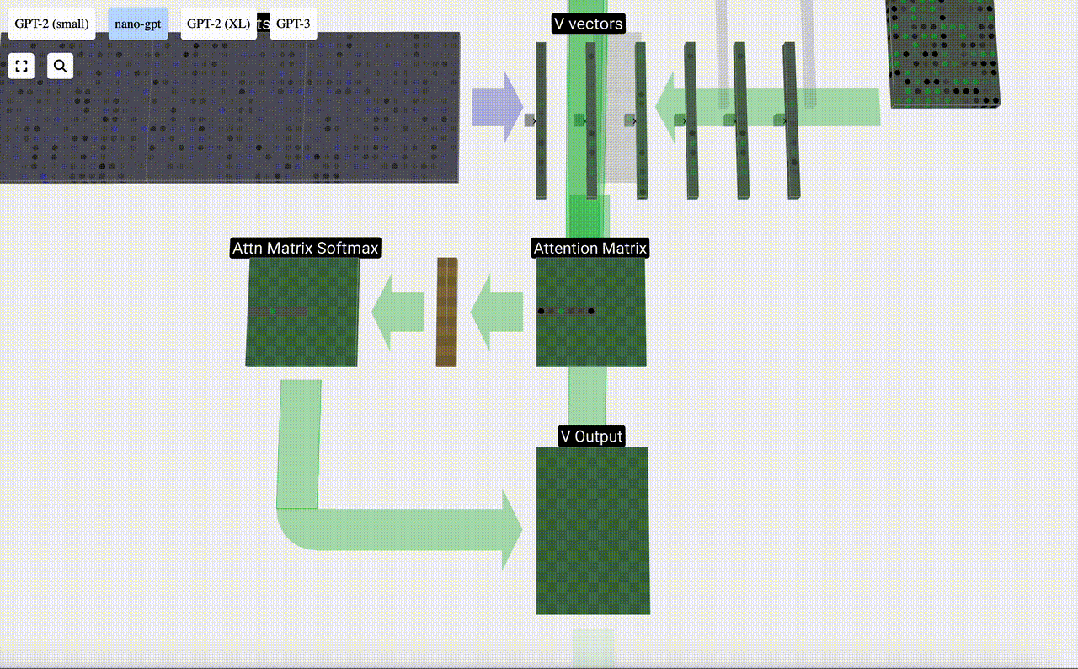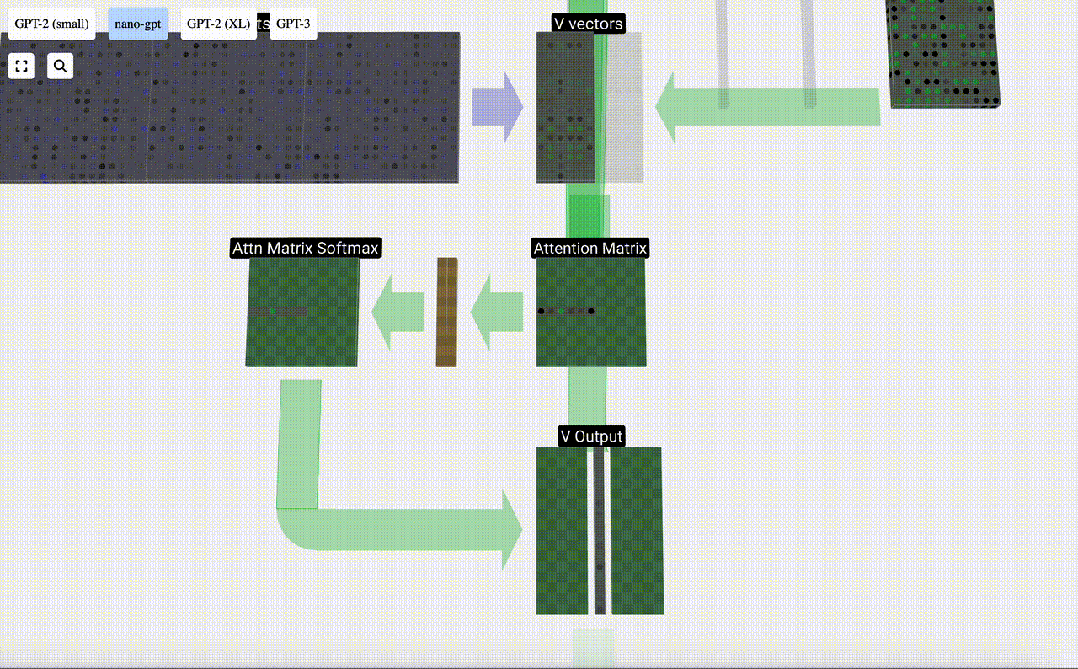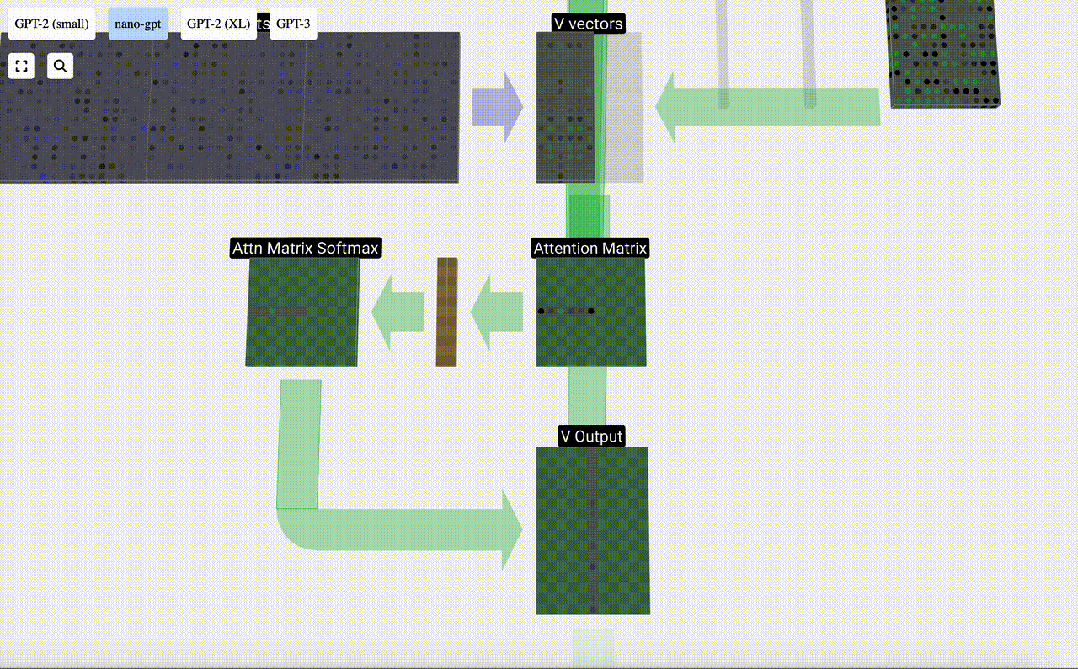
Nous pouvons ensuite ajouter ces vecteurs pour obtenir le vecteur de sortie. Par conséquent, le vecteur de sortie sera dominé par le vecteur V à haute résolution.

Maintenant, nous l'appliquons à toutes les colonnes.

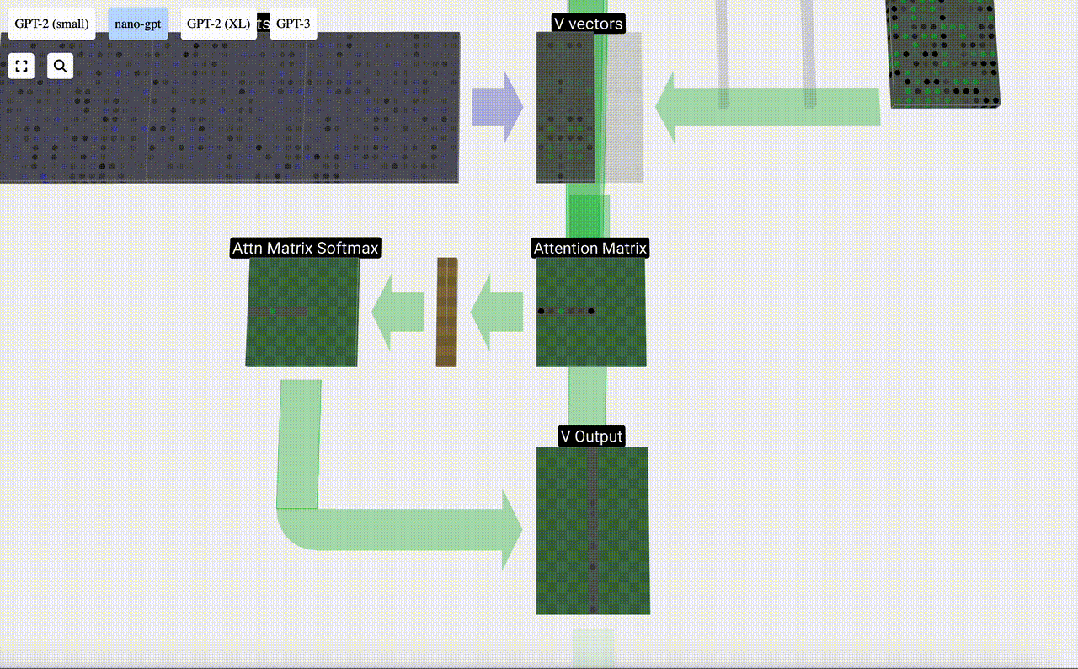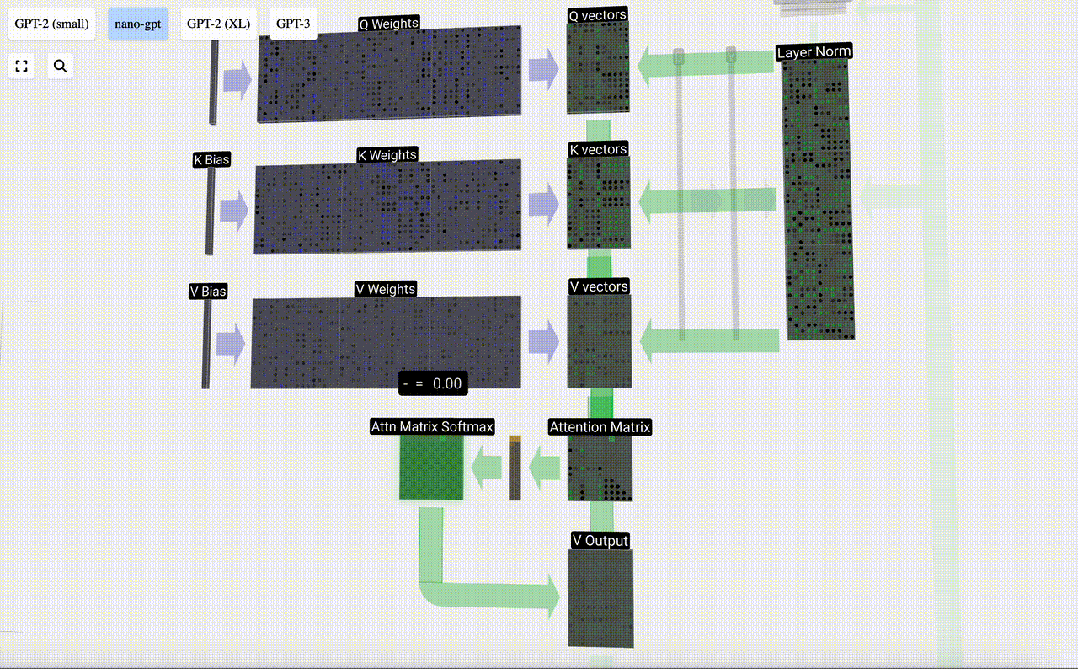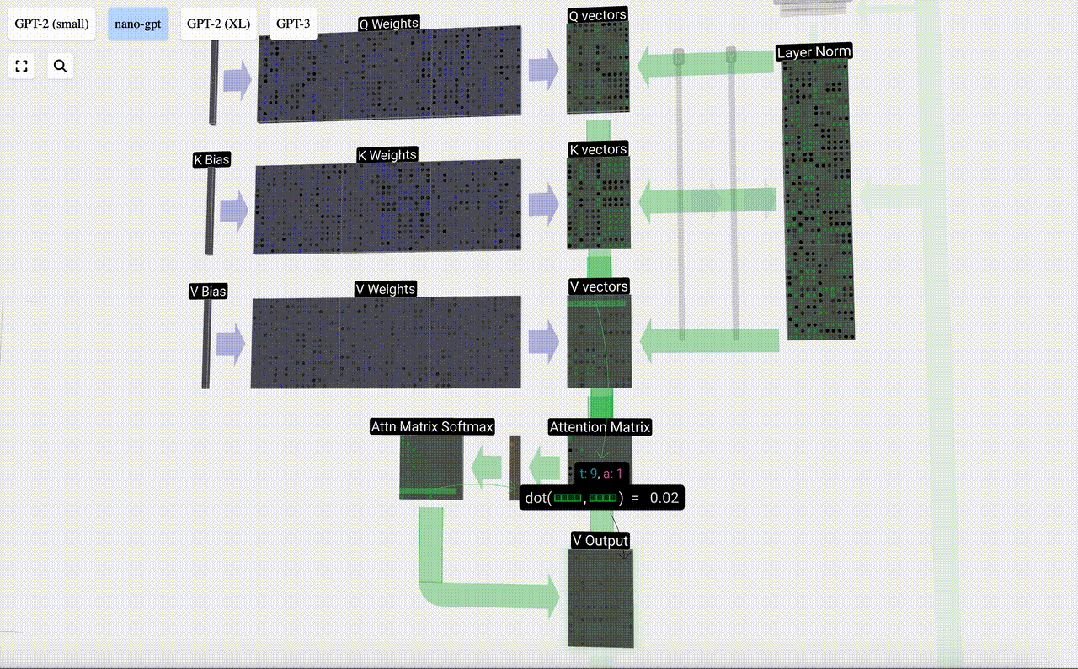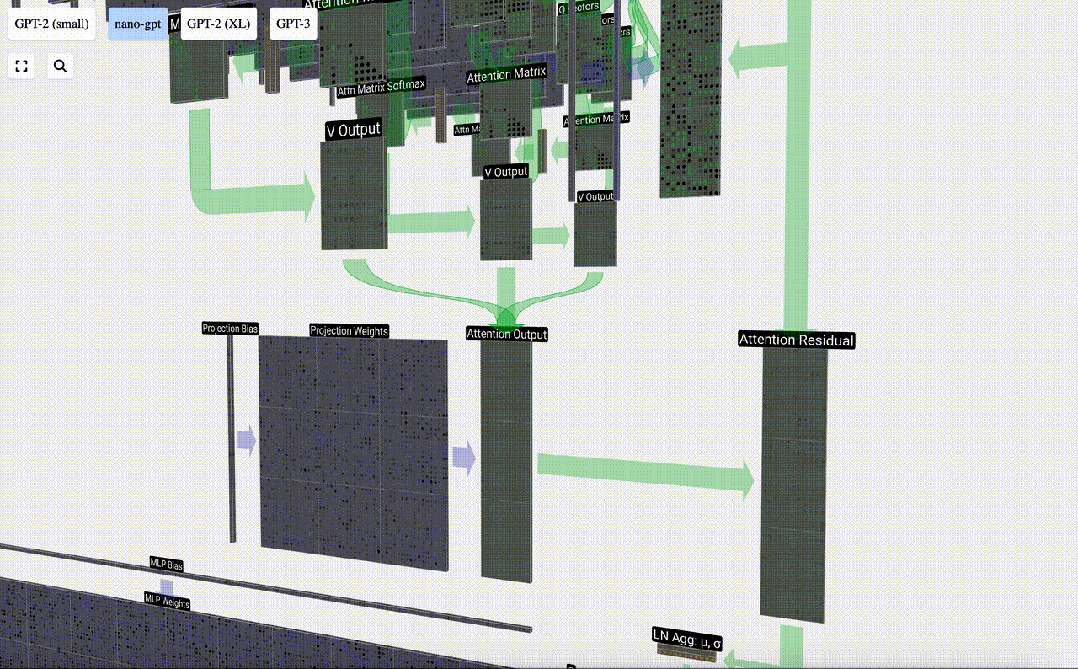
Il s'agit du processus de traitement d'un en-tête dans la couche Self Attention. "Ainsi, l'objectif principal de Self Attention est que chaque colonne souhaite trouver des informations pertinentes dans d'autres colonnes et en extraire sa valeur, et elle le fait en comparant son vecteur de requête avec les clés de ces autres colonnes. La limitation supplémentaire est qu'elle ne peut que regarder vers le passé. "

Projection

Après l'opération Self Attention, nous obtiendrons une sortie de chaque tête. Ces sorties sont des vecteurs V qui sont mélangés de manière appropriée, influencés par les vecteurs Q et K. Pour fusionner les vecteurs de sortie de chaque tête, nous les empilons simplement. Par conséquent, à t=4, nous superposerons 3 vecteurs de longueur A=16 pour former 1 vecteur de longueur C=48.

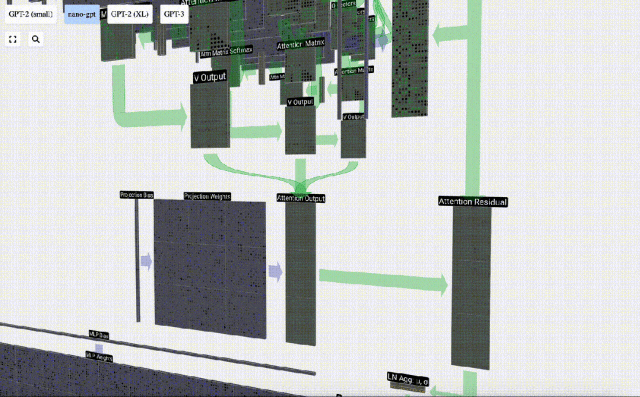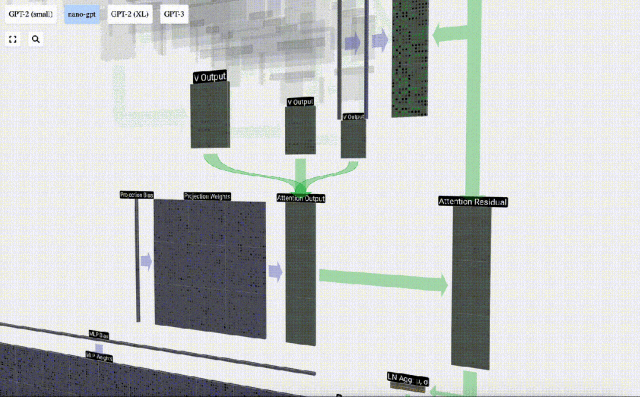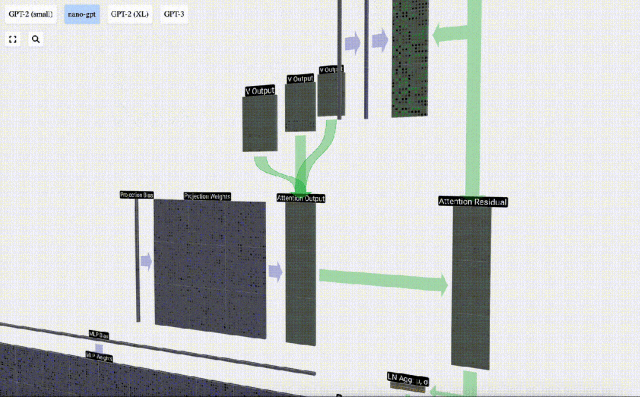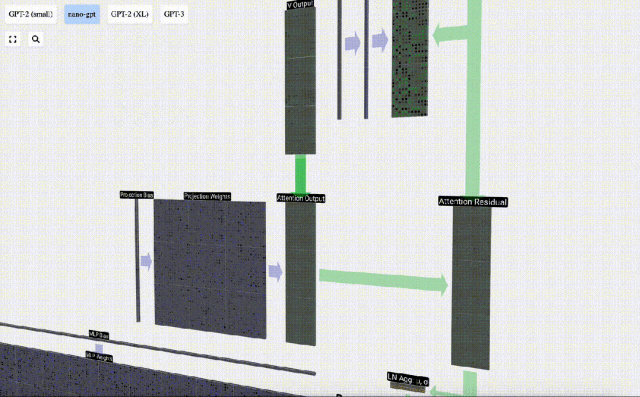
Il est à noter qu'en GPT, la longueur du vecteur à l'intérieur de la tête (A=16) est égale à C/num_heads. Cela garantit que lorsque nous les empilons ensemble, nous obtenons la longueur d'origine C.

Sur cette base, nous effectuons une projection et obtenons la sortie de cette couche. Il s'agit d'une simple multiplication matrice-vecteur, par colonne, plus un biais.

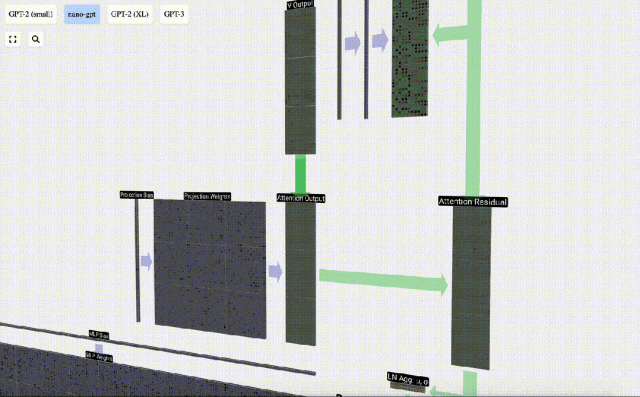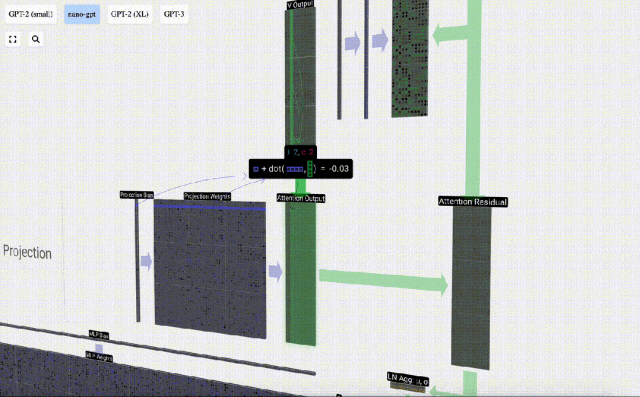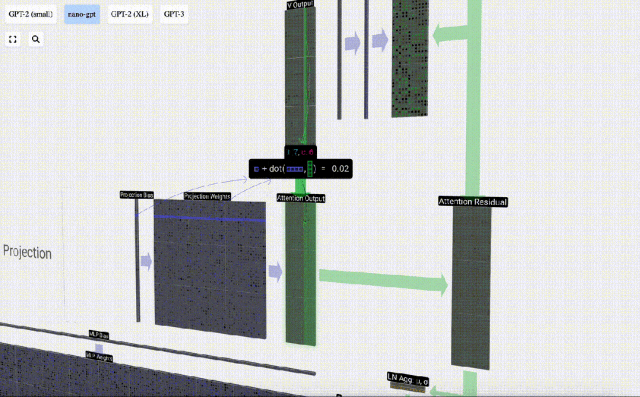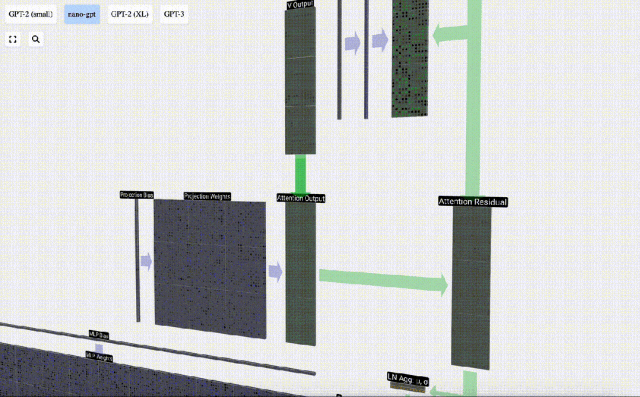
Nous avons maintenant la sortie de Self Attention.

Au lieu de transmettre cette sortie directement à l'étape suivante, nous l'ajoutons en tant qu'élément à l'intégration d'entrée. Ce processus, représenté par la flèche verticale verte, est appelé connexion résiduelle ou voie résiduelle.

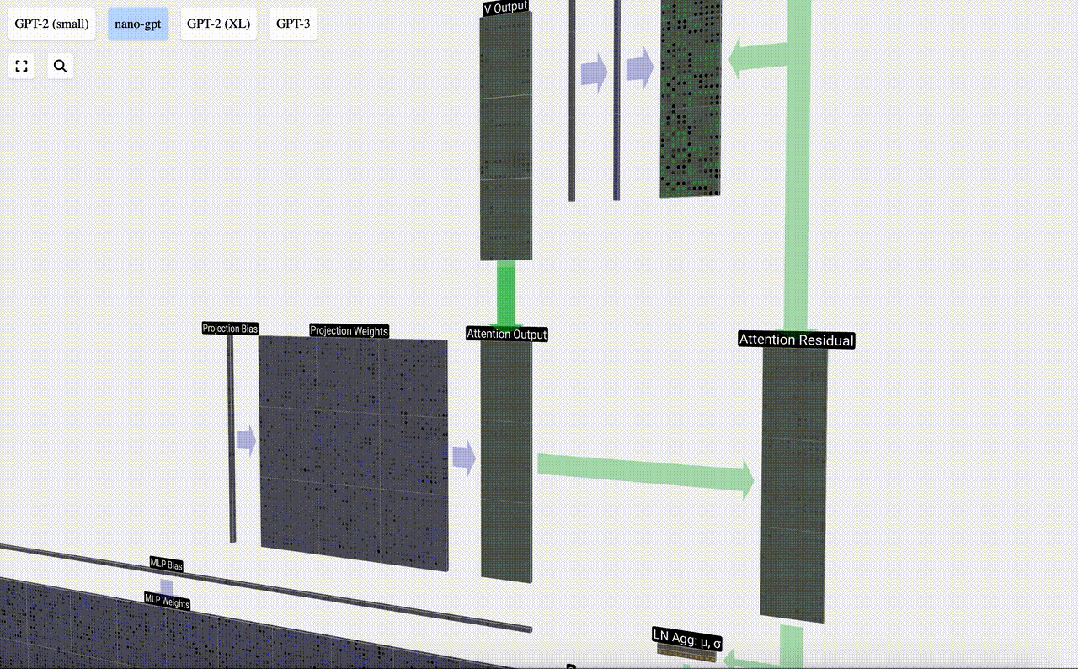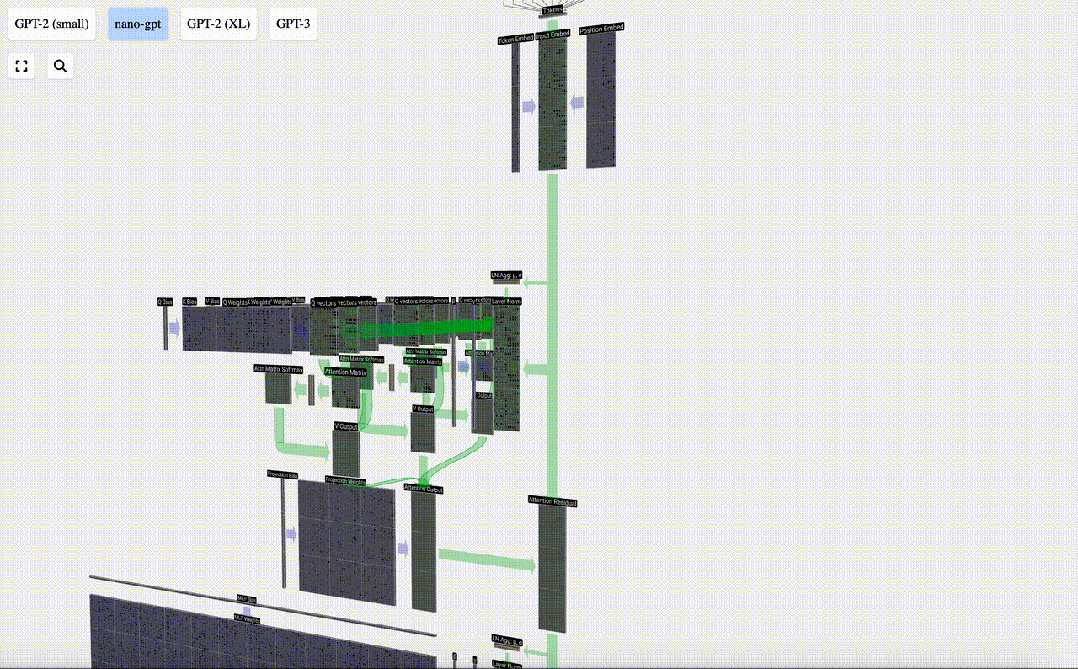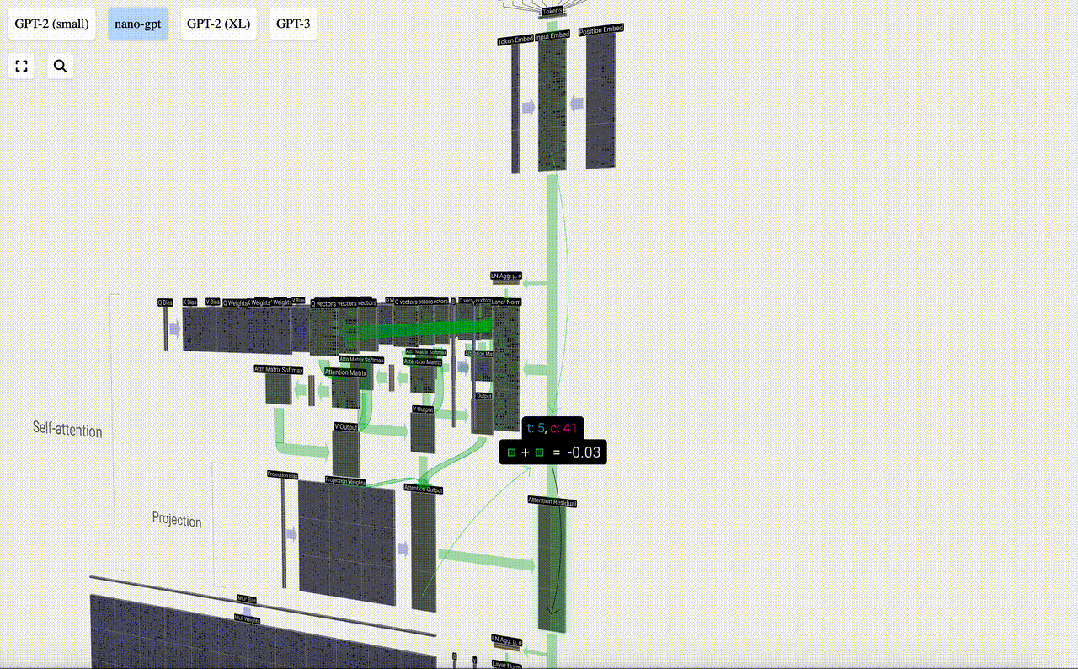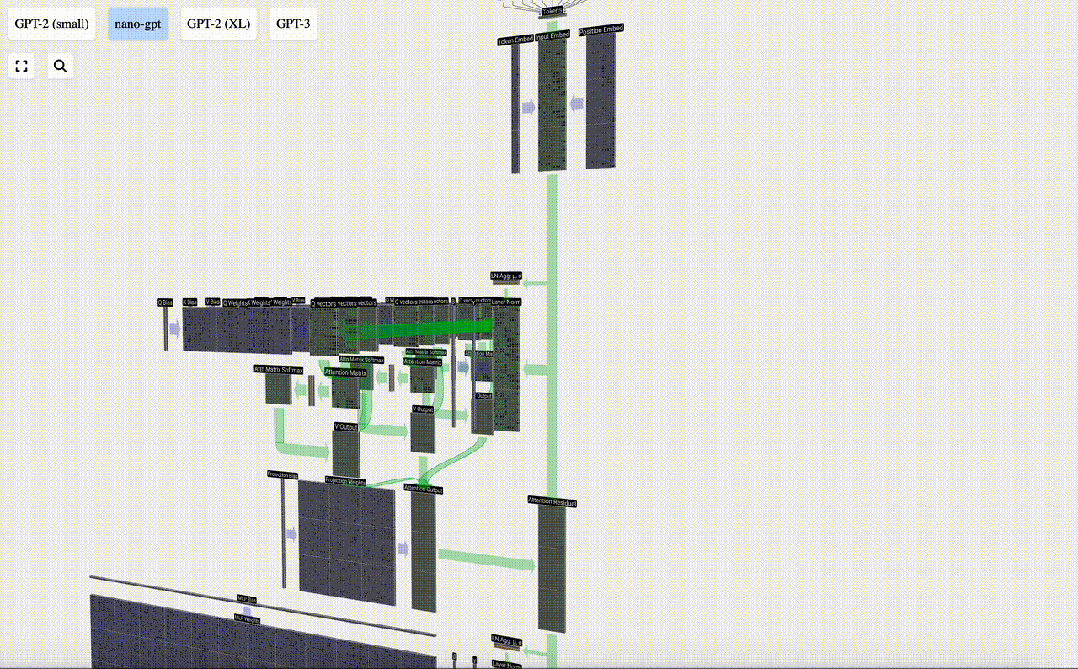
Comme la normalisation des couches, les réseaux résiduels sont cruciaux pour parvenir à un apprentissage efficace des réseaux de neurones profonds.

Maintenant que nous avons le résultat de l'auto-attention, nous pouvons le transmettre à la couche suivante de Transformer : le réseau feedforward.

Multilayer Perceptron MLP

Après Self Attention, la partie suivante du module Transformer est MLP (Multilayer Perceptron), ici il s'agit d'un simple réseau de neurones à deux couches.

Comme pour Self Attention, avant que le vecteur n'entre dans le MLP, nous devons effectuer une normalisation des couches.

En même temps, dans MLP, le traitement suivant doit être effectué (indépendamment) pour chaque vecteur colonne de longueur C=48 :

• Ajouter une transformation linéaire avec biais (c'est-à-dire une multiplication matrice-vecteur plus une opération de biais) , converti en un vecteur de longueur 4 * C.
• Fonction d'activation GELU (appliquée par élément).
• Effectuez une transformation linéaire avec biais, puis retransformez-la en un vecteur de longueur C.

Traçons l'un des vecteurs :

Le processus MLP est le suivant :

Effectuez d'abord la multiplication matrice-vecteur et ajoutez des décalages pour développer le vecteur en une matrice de longueur 4*C. (Notez que la matrice de sortie ici est transposée pour la visualisation)

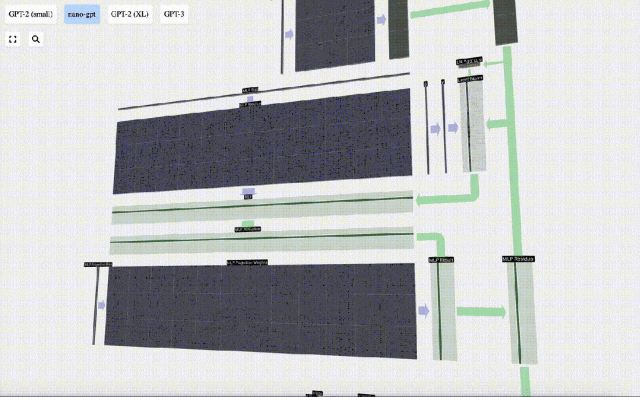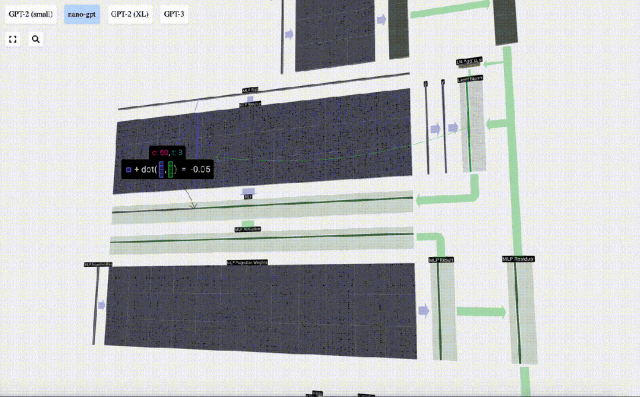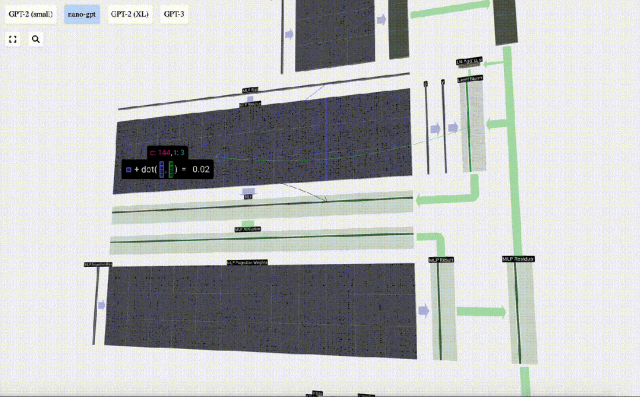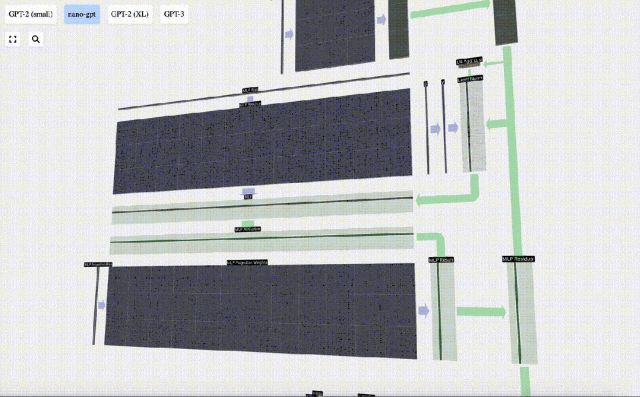
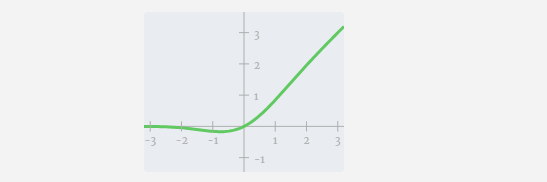
Ensuite, appliquez la fonction d'activation GELU à chaque élément du vecteur. Il s'agit d'un élément clé de tout réseau de neurones, nous devons introduire une certaine non-linéarité dans le modèle. La fonction spécifique utilisée, GELU, ressemble beaucoup à la fonction ReLU max(0, x), mais elle a une courbe douce au lieu de coins pointus.

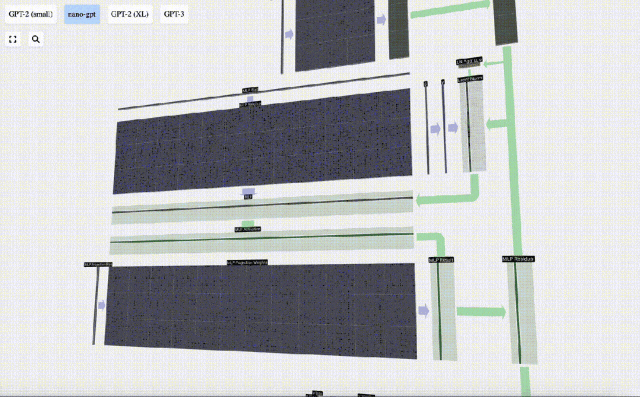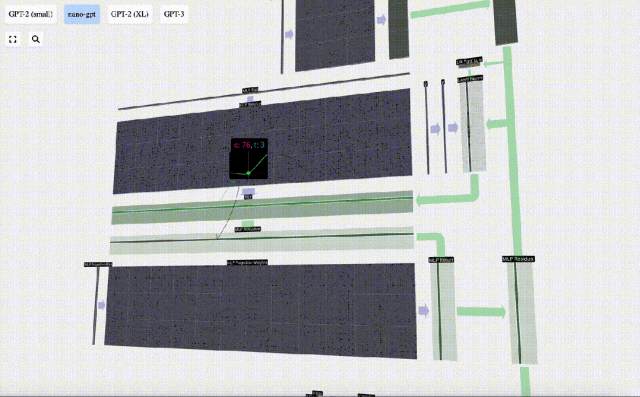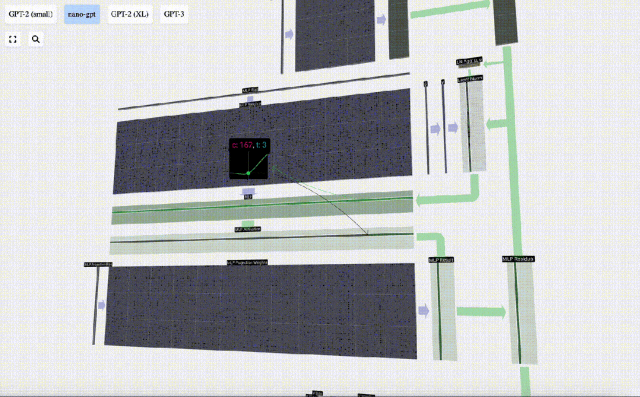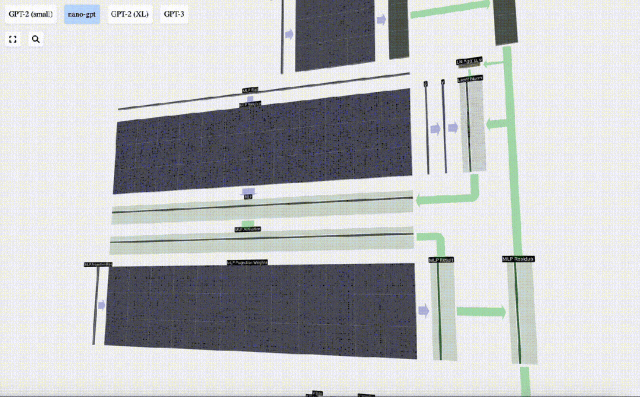
Ensuite, projetez le vecteur à la longueur C via une autre multiplication matrice-vecteur biaisée.

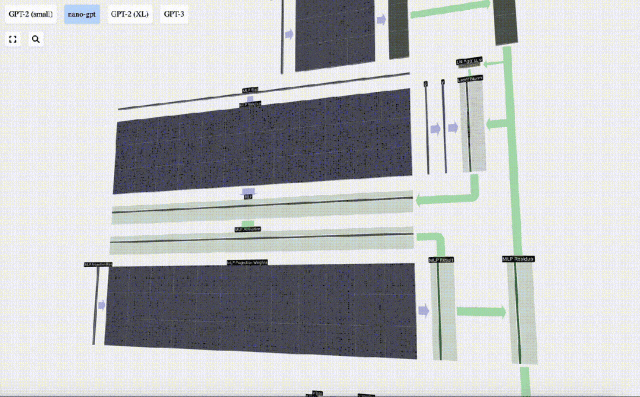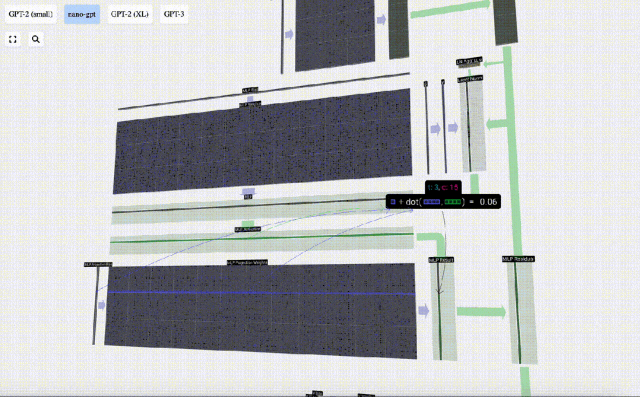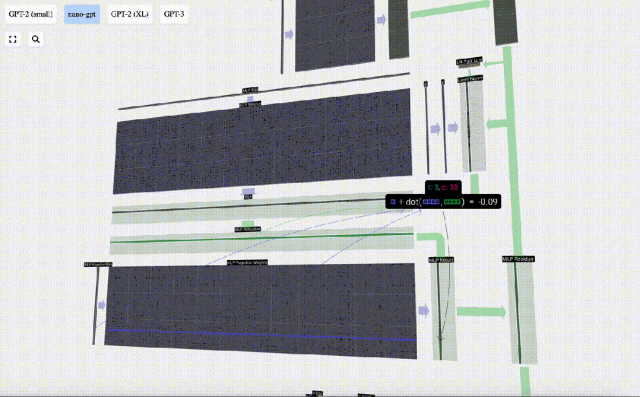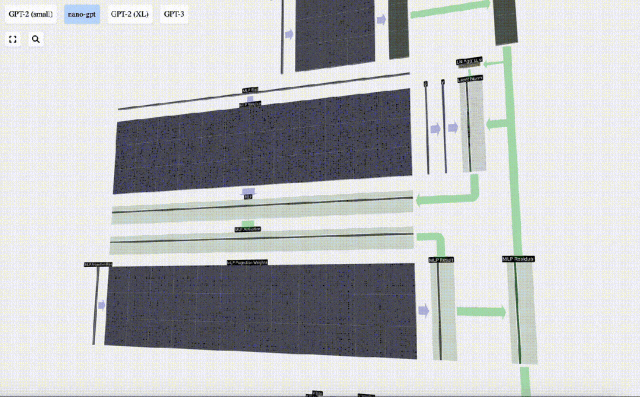
Il y a aussi un réseau résiduel ici Comme pour la partie auto-attention + projection, nous ajoutons les résultats du MLP à l'entrée dans l'ordre des éléments.

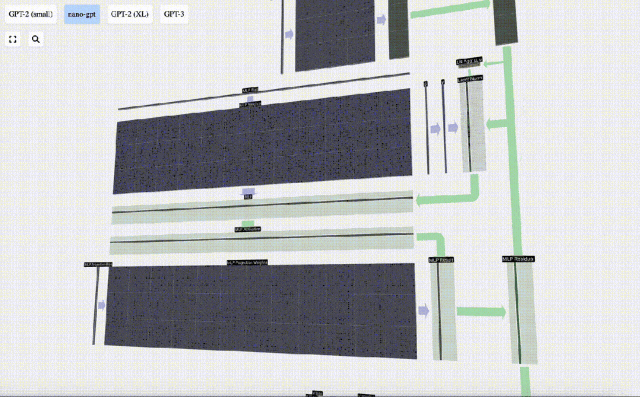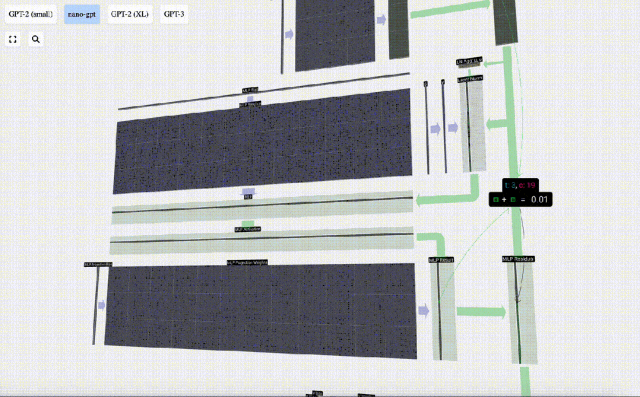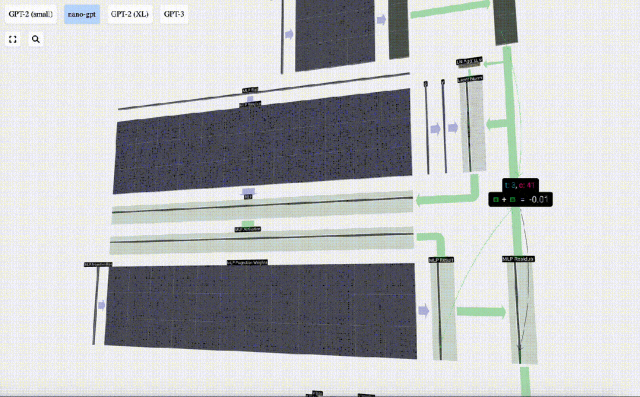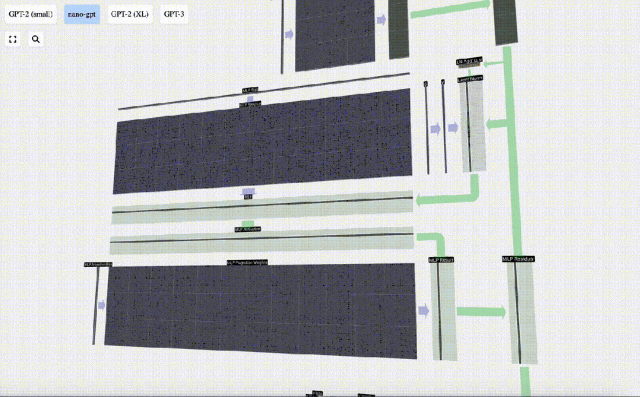
Répétez ces opérations.

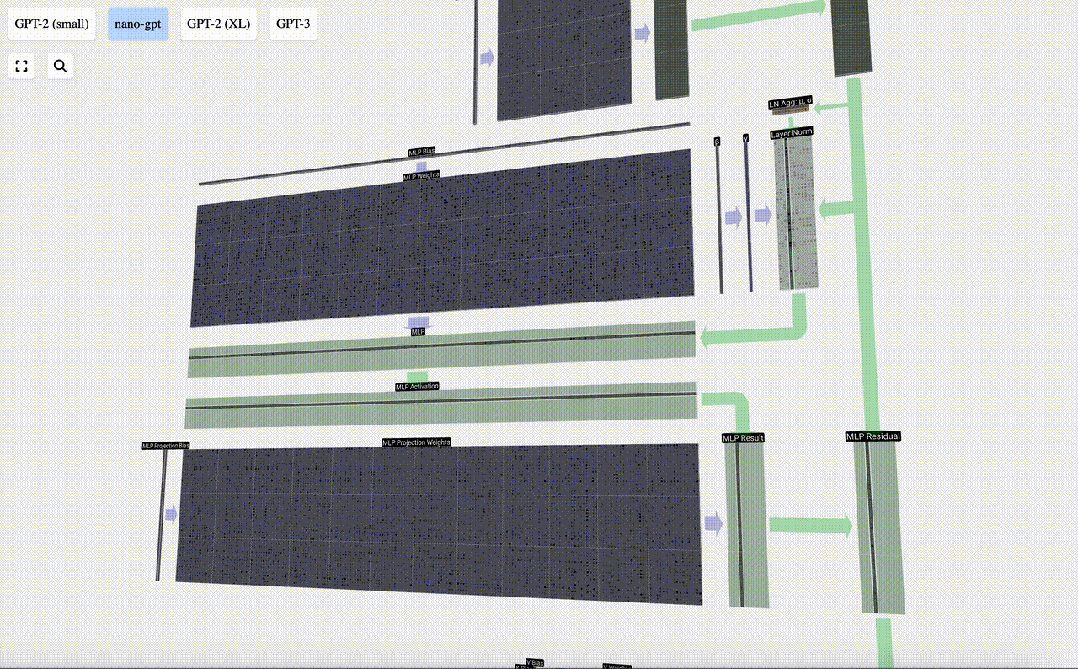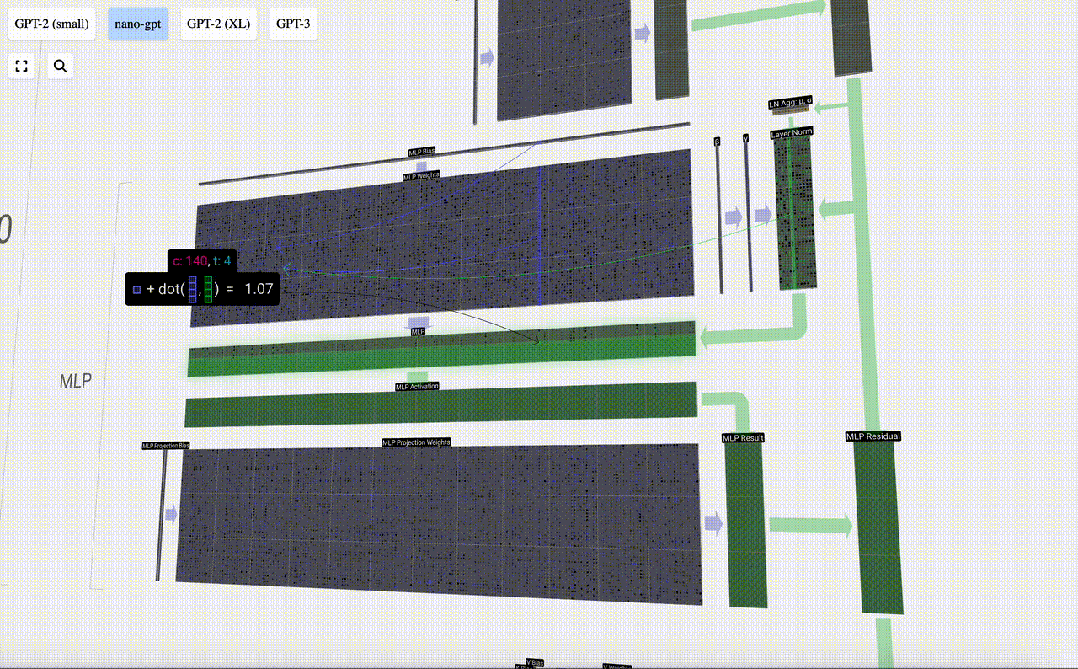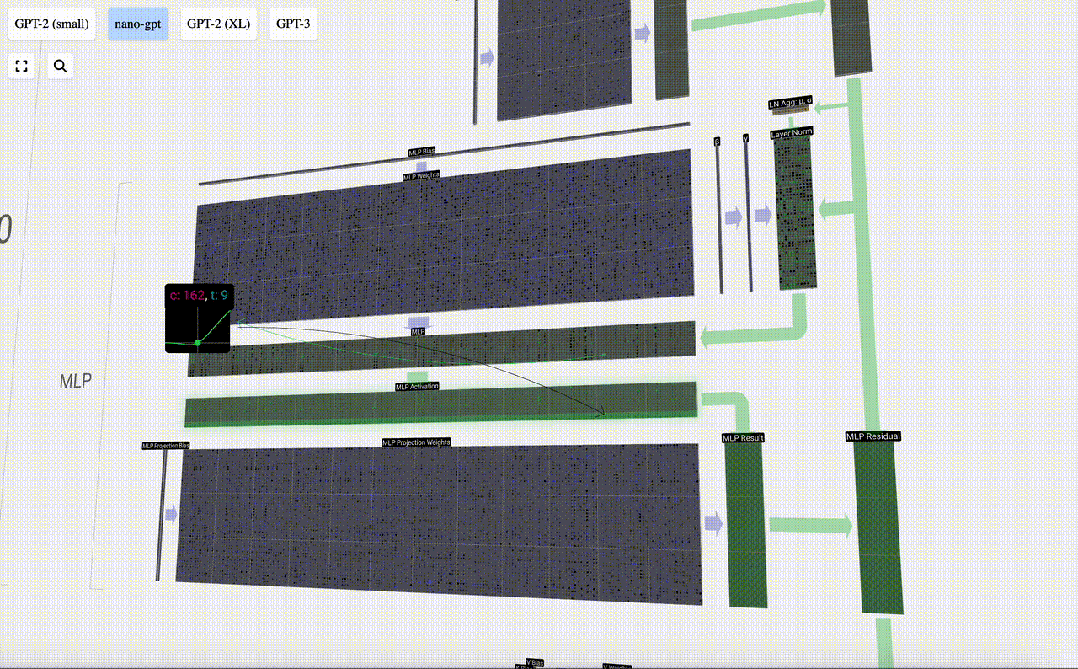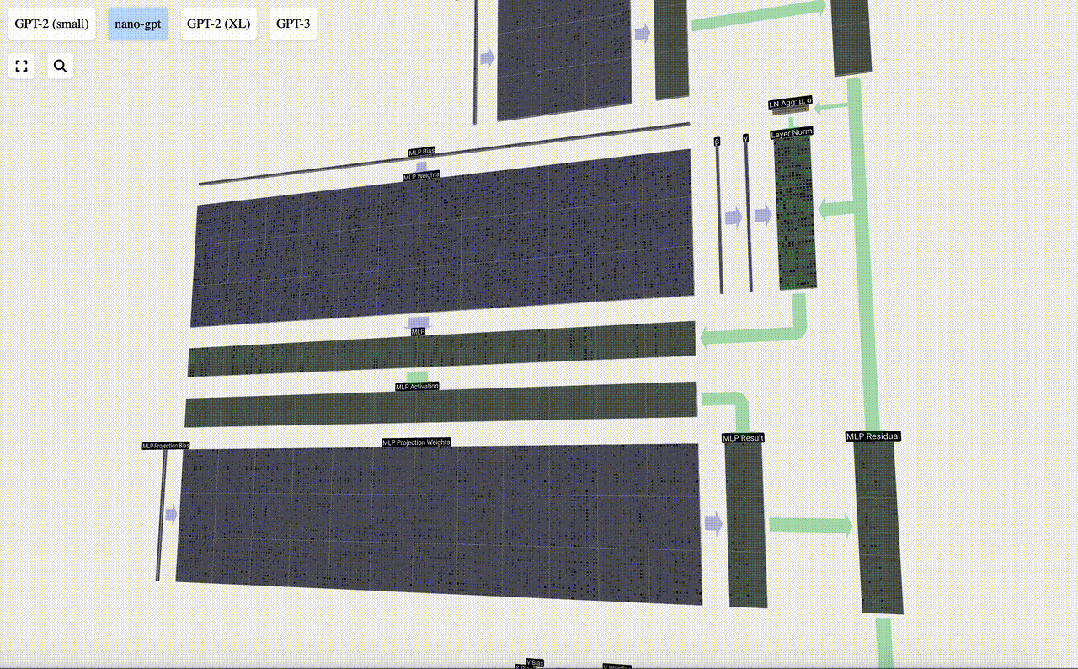
C'est la fin de la couche MLP, et on obtient enfin la sortie du transformateur.

Transformer

Il s'agit d'un module Transformer complet !

Ces plusieurs modules forment le corps principal de tout modèle GPT, et la sortie de chaque module est l'entrée du module suivant.

Comme c'est souvent le cas dans l'apprentissage profond, il est difficile de dire exactement ce que fait chacune de ces couches, mais nous avons quelques idées générales : les couches antérieures ont tendance à se concentrer sur l'apprentissage de fonctionnalités et de modèles de bas niveau, tandis que les couches ultérieures reconnaissent et comprennent les niveaux supérieurs. abstractions et relations au niveau supérieur. Dans le contexte du traitement du langage naturel, les couches inférieures peuvent apprendre la grammaire, la syntaxe et les associations lexicales simples, tandis que les couches supérieures peuvent capturer des relations sémantiques, des structures de discours et des significations dépendant du contexte plus complexes.

Softmax

La dernière étape est l'opération softmax, qui génère la probabilité prédite de chaque jeton.

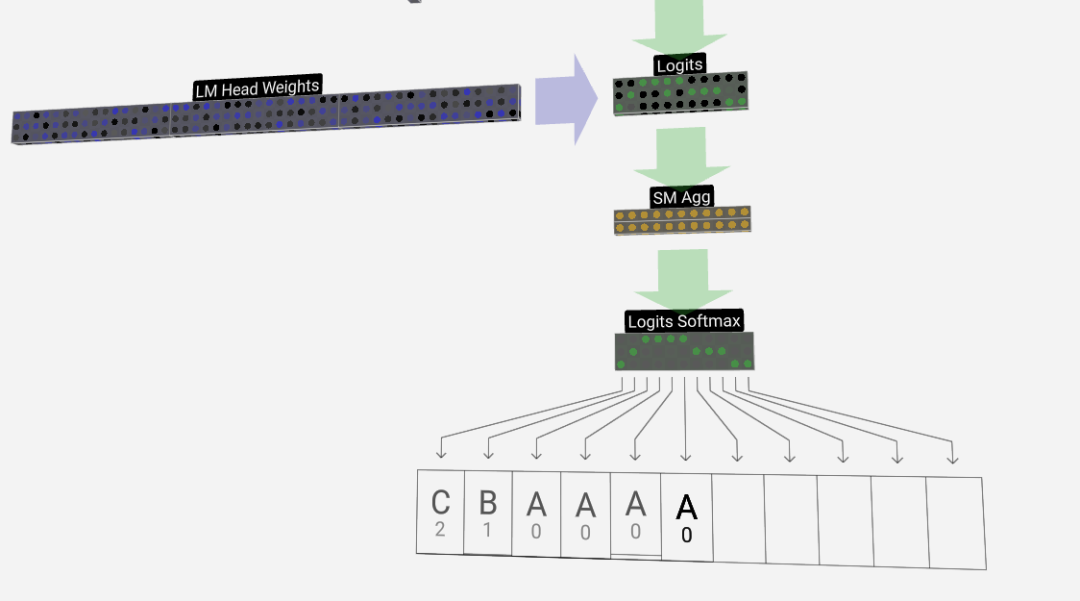
Sortie

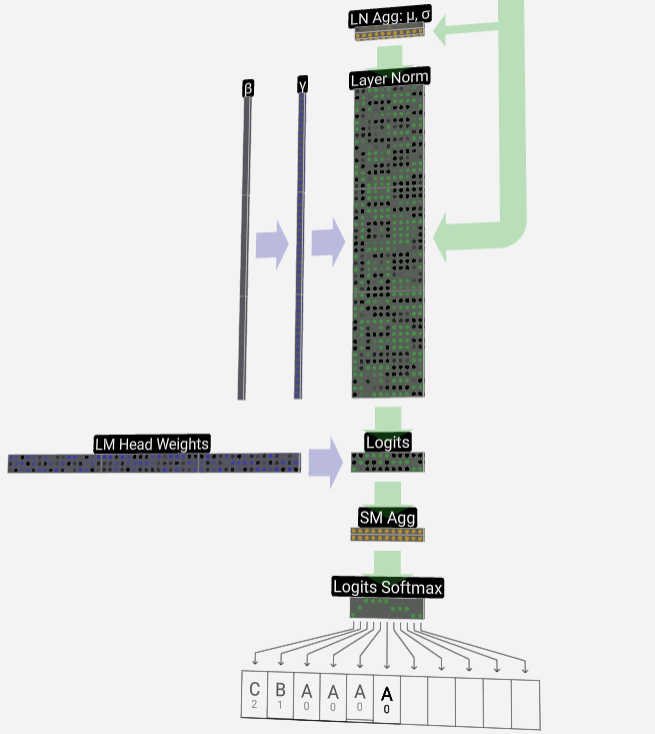
Enfin, nous arrivons à la fin du modèle. La sortie du dernier Transformer subit une couche de régularisation, suivie d'une transformation linéaire impartiale.

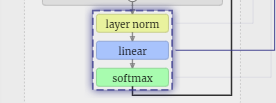
Cette transformation finale convertit chacun de nos vecteurs colonnes de la longueur C en nvocab de longueur de la taille d'un vocabulaire. Il génère donc en fait un score logits pour chaque mot du vocabulaire.

Afin de convertir ces scores en valeurs de probabilité plus intuitives, ils doivent d'abord être traités via softmax. Ainsi, pour chaque colonne, nous obtenons la probabilité que le modèle attribue à chaque mot du vocabulaire.

Dans ce modèle particulier, il a en fait appris toutes les réponses sur la façon d'ordonner les trois lettres, de sorte que les probabilités penchent fortement vers la bonne réponse.

Lorsque nous laissons le modèle avancer dans le temps, nous devons utiliser la probabilité de la dernière colonne pour décider du prochain jeton ajouté dans la séquence. Par exemple, si nous saisissons six jetons dans le modèle, nous utiliserons les probabilités de sortie de la colonne six.

Le résultat de cette colonne est une série de valeurs de probabilité, et nous devons en fait sélectionner l'une d'entre elles comme prochain jeton de la séquence. Nous y parvenons en « échantillonnant à partir de la distribution », c'est-à-dire en sélectionnant au hasard un jeton en fonction de sa probabilité. Par exemple, un jeton avec une probabilité de 0,9 a une probabilité de 90 % d'être sélectionné. Cependant, nous avons également d’autres options, comme par exemple toujours choisir le jeton ayant la probabilité la plus élevée.

On peut également contrôler la « douceur » de la distribution en utilisant le paramètre température. Des températures plus élevées rendront la distribution plus uniforme, tandis que des températures plus basses la concentreront davantage sur les jetons ayant la probabilité la plus élevée.

Nous ajustons les logits (la sortie de la transformation linéaire) en utilisant le paramètre de température avant d'appliquer softmax, car l'exponentiation dans softmax a un effet amplificateur significatif sur les valeurs plus grandes, et rapprocher toutes les valeurs réduira cet effet.

Photos

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!