 tutoriels informatiques
tutoriels informatiques
 connaissances en informatique
connaissances en informatique
 Soit la fonction fx vecteur a vecteur b vecteur c où vecteur a
Soit la fonction fx vecteur a vecteur b vecteur c où vecteur a
Soit la fonction fx vecteur a vecteur b vecteur c où vecteur a

Supposons la fonction fx vecteur a vecteur b vecteur c où vecteur a sinx
Supposons que le vecteur d(h,k)
Donc x'=x-h ; y'=y-k
x=x'-h ; y=y'-k
Ensuite, mettez la formule ci-dessus dans le F(x) d'origine
Obtenez y'-h=2+√2sin(2x-2h-3π/4)
Nous voyons maintenant la condition dans la question "rendre l'image obtenue après traduction symétrique au centre par rapport à l'origine des coordonnées"
C'est-à-dire que lorsque x=0, l'équation après la deuxième traduction est g(0)=0
Donc à cette heure -2h-3π/4=kπ
h=3π/8-kπ/2
Ensuite, nous obtenons d(3π/8-kπ/2,-2)
La clé pour répondre à cette question est de configurer le vecteur selon la méthode de traduction
Ce x'=x-h; y'=y-k
x=x'-h ; y=y'-k
f(x)=vecteur a*(b+c)
De la question f(x)=(sinx,-cosx)*(sinx-cosx,-3cosx+sinx)
f(x)=sinx(sinx-cosx)-cosx(-3cosx+sinx)
=sinxsinx-sinxcosx+3cosxcosx-sinxcosx
=sinxsins+3cosxcosx-2sinxcosx
=sinxsinx+cosxcosx+2cosxcosx-2sinxcosx
=cos2x-sin2x
=racine carrée 2/2 sin(2x+45 degrés)
Supposons la fonction fx vecteur a vecteur b c où vecteur a sinx cosx vecteur b sinx
(1)f(x)=a(b+c)=ab+ac=sinxsinx+3coxcox-2sinxcosx
=2cosxcosx-sin2x+1
=-sin2x+cos2x+2
=√2sin(2x+3π/4)+2
(2) Lorsque x appartient à [3π/8, 7π/8], 2x+3π/4 appartient à [3π/2, 5π/2]
Selon les propriétés de sinx, f(x) augmente de manière monotone à [3π/8, 7π/8]
(3) Traduisez d'abord y=cosx vers la droite par π/2 unités pour obtenir y=cos(x-π/2)=sinx
Si x reste inchangé et y augmente de √2 fois, nous obtenons y=√2sinx
Si y reste inchangé, x est réduit à 1/2 de la valeur d'origine, et nous obtenons y=√2sin(2x)
Traduisez 3π/8 unités vers la gauche et obtenez y=√2sin(2x+3π/4)
Enfin, traduisez vers le haut de 2 unités pour obtenir y=√2sin(2x+3π/4)+2
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment modifier le registre? (Avertissement: utilisez avec prudence!)
Mar 21, 2025 pm 07:46 PM
Comment modifier le registre? (Avertissement: utilisez avec prudence!)
Mar 21, 2025 pm 07:46 PM
L'article traite de l'édition du registre Windows, des précautions, des méthodes de sauvegarde et des problèmes potentiels des modifications incorrectes. Problème principal: risques d'instabilité du système et de perte de données contre les modifications inappropriées.
 Découvrez comment réparer l'avertissement de santé dans les paramètres Windows
Mar 19, 2025 am 11:10 AM
Découvrez comment réparer l'avertissement de santé dans les paramètres Windows
Mar 19, 2025 am 11:10 AM
Que signifie l'avertissement de santé des motivations dans les paramètres Windows et que devez-vous faire lorsque vous recevez l'avertissement de disque? Lisez ce tutoriel Php.CN pour obtenir des instructions étape par étape pour faire face à cette situation.
 Comment gérer les services dans Windows?
Mar 21, 2025 pm 07:52 PM
Comment gérer les services dans Windows?
Mar 21, 2025 pm 07:52 PM
L'article discute de la gestion des services Windows pour la santé du système, y compris le démarrage, l'arrêt, le redémarrage des services et les meilleures pratiques de stabilité.
 Comment utiliser l'éditeur de stratégie de groupe (gpedit.msc)?
Mar 21, 2025 pm 07:48 PM
Comment utiliser l'éditeur de stratégie de groupe (gpedit.msc)?
Mar 21, 2025 pm 07:48 PM
L'article explique comment utiliser l'éditeur de stratégie de groupe (GPedit.msc) dans Windows pour gérer les paramètres du système, en survivant les configurations courantes et les méthodes de dépannage. Il note que gpedit.msc n'est pas disponible dans Windows Home Editions, suggérant
 Comment modifier l'application par défaut pour un type de fichier?
Mar 21, 2025 pm 07:48 PM
Comment modifier l'application par défaut pour un type de fichier?
Mar 21, 2025 pm 07:48 PM
L'article discute de la modification des applications par défaut pour les types de fichiers sous Windows, y compris le retour et les modifications en vrac. Problème principal: aucune option de changement de masse intégrée.
 Metadata Windows et problèmes de services Internet: comment le résoudre?
Apr 02, 2025 pm 03:57 PM
Metadata Windows et problèmes de services Internet: comment le résoudre?
Apr 02, 2025 pm 03:57 PM
Vous pouvez voir que «une connexion aux métadonnées Windows et aux services Internet (WMIS) n'a pas pu être établie.» Erreur sur la visionneuse d'événements. Cet article de Php.cn présente comment supprimer le problème des métadonnées Windows et des services Internet.
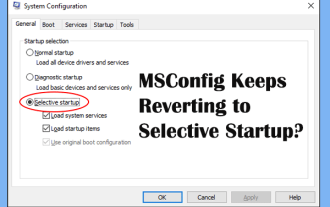 MSConfig continue de revenir au démarrage sélectif? 2 solutions ici
Mar 28, 2025 pm 12:06 PM
MSConfig continue de revenir au démarrage sélectif? 2 solutions ici
Mar 28, 2025 pm 12:06 PM
Êtes-vous interrogé sur un problème que MSConfig continue de revenir au démarrage sélectif sur vos fenêtres? Comment passer au démarrage normal si vous en avez besoin? Essayez les méthodes expliquées dans ce post php.cn pour en trouver une qui fonctionne pour vous.
 Comment créer un raccourci clavier personnalisé?
Mar 21, 2025 pm 07:47 PM
Comment créer un raccourci clavier personnalisé?
Mar 21, 2025 pm 07:47 PM
L'article discute de la création de raccourcis clavier personnalisés sur Windows et MacOS, en utilisant des logiciels comme AutoHotKey et le clavier Maestro, et le dépannage des méthodes si les raccourcis échouent.





