
Soit theta = paramètres du modèle et max_iters = nombre d'époques. Pour itr=1,2,3,...,max_iters : Pour mini_batch(X_mini,y_mini) :
Passage direct du lot X_mini :
1 Prédisez le mini-lot
2. des paramètres Calculer l'erreur de prédiction (J(theta))
Post-transmission : Calculer le gradient (theta)=J(theta) par rapport à la dérivée partielle de theta
Mettre à jour les paramètres : theta=theta–learning_rate*gradient(theta )
Étape 1 : importez les dépendances, générez des données pour la régression linéaire et visualisez les données générées. Prenez 8 000 exemples de données, chaque exemple possède 2 caractéristiques d'attribut. Ces échantillons de données sont ensuite divisés en ensemble d'apprentissage (X_train, y_train) et ensemble de test (X_test, y_test), avec respectivement 7 200 et 800 échantillons.
import numpy as np import matplotlib.pyplot as plt mean=np.array([5.0,6.0]) cov=np.array([[1.0,0.95],[0.95,1.2]]) data=np.random.multivariate_normal(mean,cov,8000) plt.scatter(data[:500,0],data[:500,1],marker='.') plt.show() data=np.hstack((np.ones((data.shape[0],1)),data)) split_factor=0.90 split=int(split_factor*data.shape[0]) X_train=data[:split,:-1] y_train=data[:split,-1].reshape((-1,1)) X_test=data[split:,:-1] y_test=data[split:,-1].reshape((-1,1)) print(& quot Number of examples in training set= % d & quot % (X_train.shape[0])) print(& quot Number of examples in testing set= % d & quot % (X_test.shape[0]))
Nombre d'exemples dans l'ensemble d'entraînement = 7200 Nombre d'exemples dans l'ensemble de test = 800
Étape 2 :
Code pour implémenter la régression linéaire en utilisant la descente de gradient par mini-lots. gradientDescent() est la fonction motrice principale, et d'autres fonctions sont des fonctions auxiliaires :
Faire des prédictions - hypothese()
Calculer le dégradé - gradient()
Calculer l'erreur - cost()
Créer des mini lots - create_mini_batches ( )
La fonction pilote initialise les paramètres, calcule l'ensemble optimal de paramètres pour le modèle et renvoie ces paramètres ainsi qu'une liste contenant l'historique des erreurs au fur et à mesure de la mise à jour des paramètres.
def hypothesis(X,theta):
return np.dot(X,theta)
def gradient(X,y,theta):
h=hypothesis(X,theta)
grad=np.dot(X.transpose(),(h-y))
return grad
def cost(X,y,theta):
h=hypothesis(X,theta)
J=np.dot((h-y).transpose(),(h-y))
J/=2
return J[0]
def create_mini_batches(X,y,batch_size):
mini_batches=[]
data=np.hstack((X,y))
np.random.shuffle(data)
n_minibatches=data.shape[0]//batch_size
i=0
for i in range(n_minibatches+1):
mini_batch=data[i*batch_size:(i+1)*batch_size,:]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
if data.shape[0]%batch_size!=0:
mini_batch=data[i*batch_size:data.shape[0]]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
return mini_batches
def gradientDescent(X,y,learning_rate=0.001,batch_size=32):
theta=np.zeros((X.shape[1],1))
error_list=[]
max_iters=3
for itr in range(max_iters):
mini_batches=create_mini_batches(X,y,batch_size)
for mini_batch in mini_batches:
X_mini,y_mini=mini_batch
theta=theta-learning_rate*gradient(X_mini,y_mini,theta)
error_list.append(cost(X_mini,y_mini,theta))
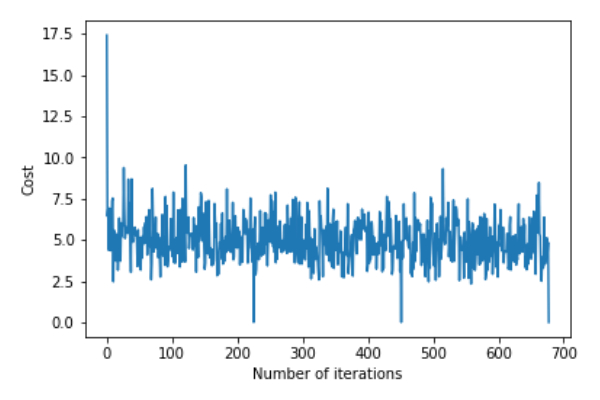
return theta,error_listAppelez la fonction gradientDescent() pour calculer les paramètres du modèle (thêta) et visualiser les changements dans la fonction d'erreur.
theta,error_list=gradientDescent(X_train,y_train)
print("Bias=",theta[0])
print("Coefficients=",theta[1:])
plt.plot(error_list)
plt.xlabel("Number of iterations")
plt.ylabel("Cost")
plt.show()Deviation=[0.81830471]Coefficient=[[1.04586595]]
Étape 3 : Prédisez l'ensemble de test et calculez l'erreur absolue moyenne dans la prédiction.
y_pred=hypothesis(X_test,theta) plt.scatter(X_test[:,1],y_test[:,],marker='.') plt.plot(X_test[:,1],y_pred,color='orange') plt.show() error=np.sum(np.abs(y_test-y_pred)/y_test.shape[0]) print(& quot Mean absolute error=",error)
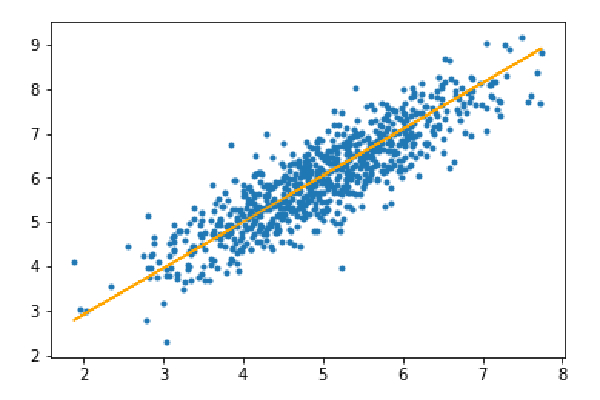
Erreur absolue moyenne=0,4366644295854125
La ligne orange représente la fonction d'hypothèse finale : theta[0]+theta[1]*X_test[:,1]+theta[2]*X_test[:,2]=0
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 collection de codes HTML
collection de codes HTML
 Quel est le format du nom de compte de Steam
Quel est le format du nom de compte de Steam
 Comment mettre à jour le pilote de la carte graphique
Comment mettre à jour le pilote de la carte graphique
 Introduction au document en JS
Introduction au document en JS
 Logiciel gratuit de récupération de données
Logiciel gratuit de récupération de données
 Comment résoudre l'incompatibilité de charge du serveur
Comment résoudre l'incompatibilité de charge du serveur
 commutateur proxy
commutateur proxy
 Raisons pour lesquelles le chargement du CSS a échoué
Raisons pour lesquelles le chargement du CSS a échoué