base de données
tutoriel mysql
Utiliser Python pour écrire le code de l'opération de suppression de l'arbre B+
Utiliser Python pour écrire le code de l'opération de suppression de l'arbre B+
L'opération de suppression d'arborescence B+ nécessite d'abord de trouver l'emplacement du nœud supprimé, puis de déterminer le nombre de clés du nœud.
Si le nombre de clés dans le nœud dépasse le nombre minimum, supprimez-le simplement directement.
Comme indiqué ci-dessous, supprimez "40" :
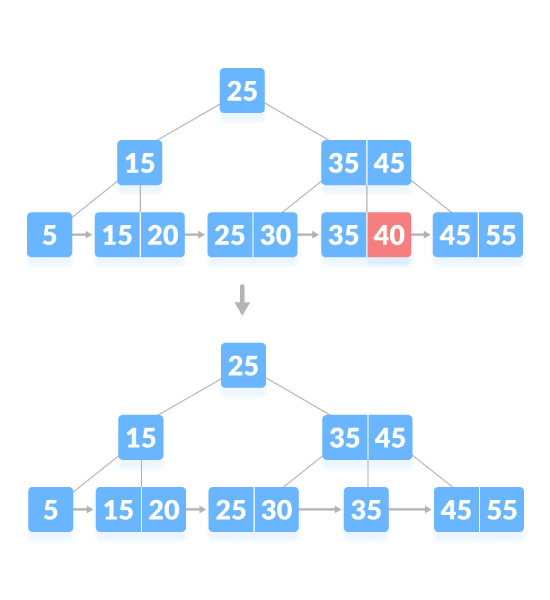
S'il y a un nombre minimum exact de clés dans le nœud, la suppression nécessite d'emprunter au nœud frère et d'ajouter la clé intermédiaire du nœud frère au nœud parent. Comme indiqué ci-dessous, supprimez "5":
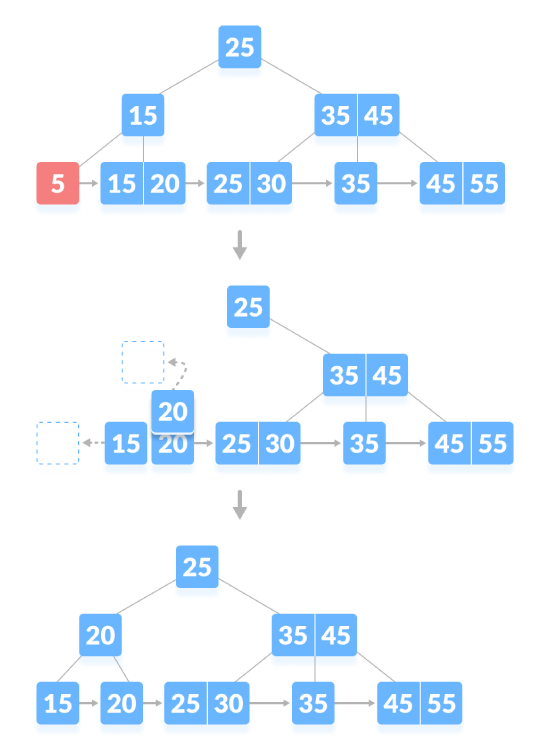
Supprimez le nœud de contenu, si le nombre de clés dans le nœud dépasse le nombre minimum, supprimez simplement la clé du nœud feuille et supprimez la clé du nœud interne . Remplissez les espaces vides dans les nœuds internes avec des successeurs dans l'ordre. Comme indiqué ci-dessous, supprimez "45":
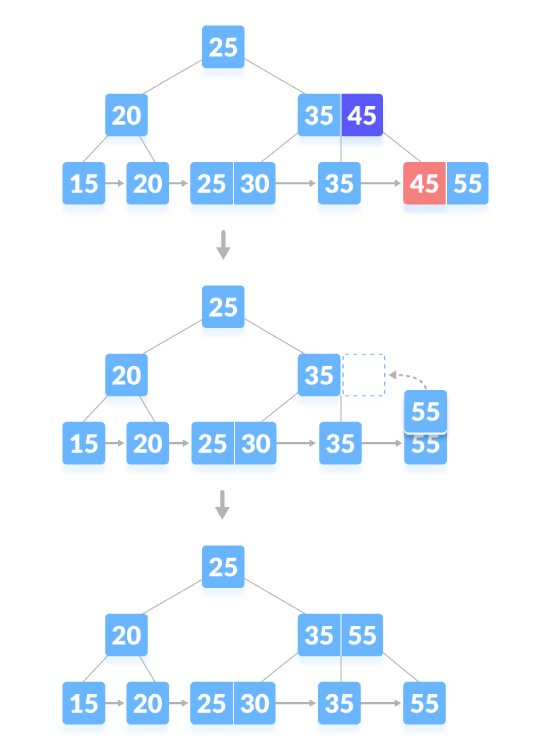
Supprimez le nœud de contenu, s'il y a un nombre minimum exact de clés dans le nœud, supprimez la clé et empruntez une clé directement au nœud frère, et remplissez le index avec la clé empruntée de l'espace vide. Comme indiqué ci-dessous, supprimez "35" :
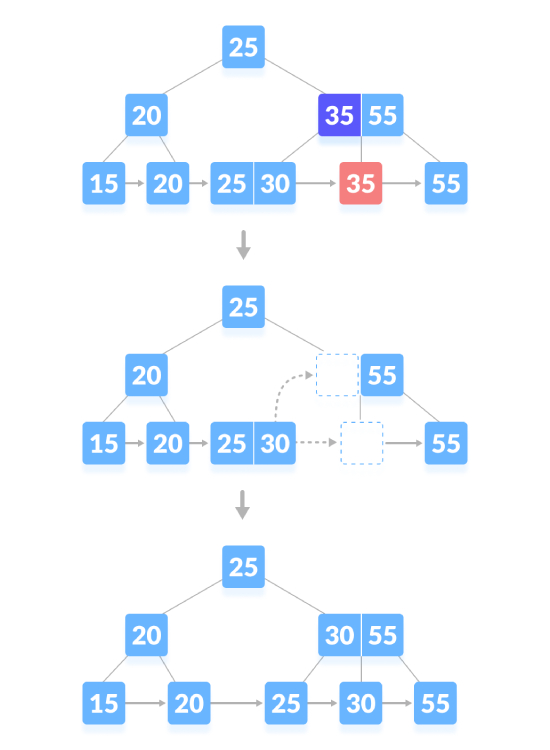
Supprimez le nœud de contenu et générez un espace vide au-dessus du nœud parent. Après avoir supprimé une clé, fusionnez l'espace vide avec ses frères et sœurs, en remplissant l'espace vide du nœud parent avec le successeur dans l'ordre. Comme indiqué ci-dessous, supprimez "25":
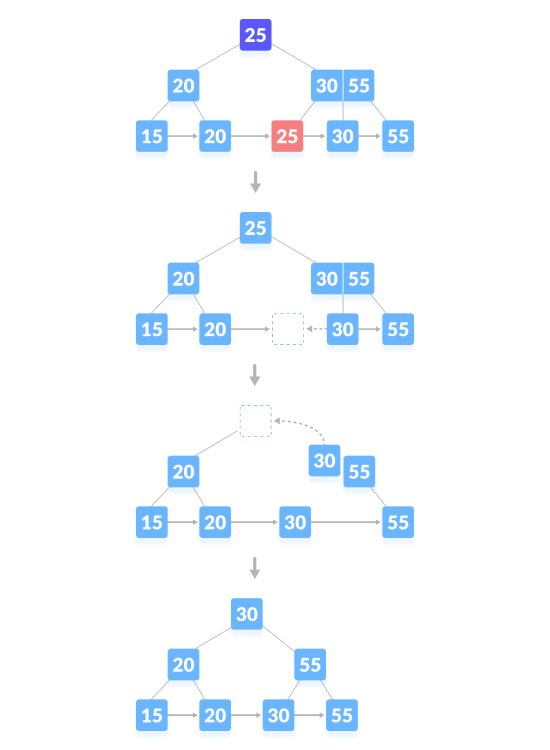
L'opération de suppression qui provoque la réduction de la hauteur de l'arbre, comme indiqué ci-dessous, supprimez "55":
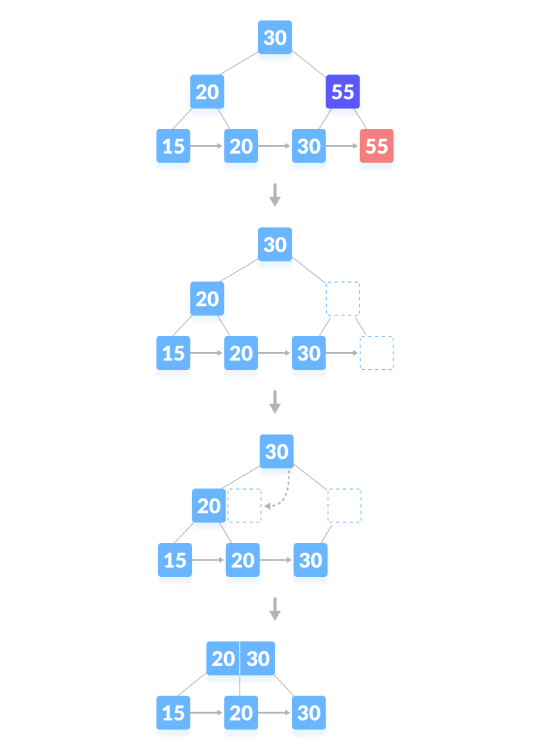
Python implémente l'opération de suppression d'arbre B+
import math
# 创建节点
class Node:
def __init__(self, order):
self.order = order
self.values = []
self.keys = []
self.nextKey = None
self.parent = None
self.check_leaf = False
# 插入叶子
def insert_at_leaf(self, leaf, value, key):
if (self.values):
temp1 = self.values
for i in range(len(temp1)):
if (value == temp1[i]):
self.keys[i].append(key)
break
elif (value < temp1[i]):
self.values = self.values[:i] + [value] + self.values[i:]
self.keys = self.keys[:i] + [[key]] + self.keys[i:]
break
elif (i + 1 == len(temp1)):
self.values.append(value)
self.keys.append([key])
break
else:
self.values = [value]
self.keys = [[key]]
# B+树
class BplusTree:
def __init__(self, order):
self.root = Node(order)
self.root.check_leaf = True
# 插入节点
def insert(self, value, key):
value = str(value)
old_node = self.search(value)
old_node.insert_at_leaf(old_node, value, key)
if (len(old_node.values) == old_node.order):
node1 = Node(old_node.order)
node1.check_leaf = True
node1.parent = old_node.parent
mid = int(math.ceil(old_node.order / 2)) - 1
node1.values = old_node.values[mid + 1:]
node1.keys = old_node.keys[mid + 1:]
node1.nextKey = old_node.nextKey
old_node.values = old_node.values[:mid + 1]
old_node.keys = old_node.keys[:mid + 1]
old_node.nextKey = node1
self.insert_in_parent(old_node, node1.values[0], node1)
def search(self, value):
current_node = self.root
while(current_node.check_leaf == False):
temp2 = current_node.values
for i in range(len(temp2)):
if (value == temp2[i]):
current_node = current_node.keys[i + 1]
break
elif (value < temp2[i]):
current_node = current_node.keys[i]
break
elif (i + 1 == len(current_node.values)):
current_node = current_node.keys[i + 1]
break
return current_node
# 查找节点
def find(self, value, key):
l = self.search(value)
for i, item in enumerate(l.values):
if item == value:
if key in l.keys[i]:
return True
else:
return False
return False
# 在父级插入
def insert_in_parent(self, n, value, ndash):
if (self.root == n):
rootNode = Node(n.order)
rootNode.values = [value]
rootNode.keys = [n, ndash]
self.root = rootNode
n.parent = rootNode
ndash.parent = rootNode
return
parentNode = n.parent
temp3 = parentNode.keys
for i in range(len(temp3)):
if (temp3[i] == n):
parentNode.values = parentNode.values[:i] + \
[value] + parentNode.values[i:]
parentNode.keys = parentNode.keys[:i +
1] + [ndash] + parentNode.keys[i + 1:]
if (len(parentNode.keys) > parentNode.order):
parentdash = Node(parentNode.order)
parentdash.parent = parentNode.parent
mid = int(math.ceil(parentNode.order / 2)) - 1
parentdash.values = parentNode.values[mid + 1:]
parentdash.keys = parentNode.keys[mid + 1:]
value_ = parentNode.values[mid]
if (mid == 0):
parentNode.values = parentNode.values[:mid + 1]
else:
parentNode.values = parentNode.values[:mid]
parentNode.keys = parentNode.keys[:mid + 1]
for j in parentNode.keys:
j.parent = parentNode
for j in parentdash.keys:
j.parent = parentdash
self.insert_in_parent(parentNode, value_, parentdash)
# 删除节点
def delete(self, value, key):
node_ = self.search(value)
temp = 0
for i, item in enumerate(node_.values):
if item == value:
temp = 1
if key in node_.keys[i]:
if len(node_.keys[i]) > 1:
node_.keys[i].pop(node_.keys[i].index(key))
elif node_ == self.root:
node_.values.pop(i)
node_.keys.pop(i)
else:
node_.keys[i].pop(node_.keys[i].index(key))
del node_.keys[i]
node_.values.pop(node_.values.index(value))
self.deleteEntry(node_, value, key)
else:
print("Value not in Key")
return
if temp == 0:
print("Value not in Tree")
return
# 删除条目
def deleteEntry(self, node_, value, key):
if not node_.check_leaf:
for i, item in enumerate(node_.keys):
if item == key:
node_.keys.pop(i)
break
for i, item in enumerate(node_.values):
if item == value:
node_.values.pop(i)
break
if self.root == node_ and len(node_.keys) == 1:
self.root = node_.keys[0]
node_.keys[0].parent = None
del node_
return
elif (len(node_.keys) < int(math.ceil(node_.order / 2)) and node_.check_leaf == False) or (len(node_.values) < int(math.ceil((node_.order - 1) / 2)) and node_.check_leaf == True):
is_predecessor = 0
parentNode = node_.parent
PrevNode = -1
NextNode = -1
PrevK = -1
PostK = -1
for i, item in enumerate(parentNode.keys):
if item == node_:
if i > 0:
PrevNode = parentNode.keys[i - 1]
PrevK = parentNode.values[i - 1]
if i < len(parentNode.keys) - 1:
NextNode = parentNode.keys[i + 1]
PostK = parentNode.values[i]
if PrevNode == -1:
ndash = NextNode
value_ = PostK
elif NextNode == -1:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
else:
if len(node_.values) + len(NextNode.values) < node_.order:
ndash = NextNode
value_ = PostK
else:
is_predecessor = 1
ndash = PrevNode
value_ = PrevK
if len(node_.values) + len(ndash.values) < node_.order:
if is_predecessor == 0:
node_, ndash = ndash, node_
ndash.keys += node_.keys
if not node_.check_leaf:
ndash.values.append(value_)
else:
ndash.nextKey = node_.nextKey
ndash.values += node_.values
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
self.deleteEntry(node_.parent, value_, node_)
del node_
else:
if is_predecessor == 1:
if not node_.check_leaf:
ndashpm = ndash.keys.pop(-1)
ndashkm_1 = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [value_] + node_.values
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
p.values[i] = ndashkm_1
break
else:
ndashpm = ndash.keys.pop(-1)
ndashkm = ndash.values.pop(-1)
node_.keys = [ndashpm] + node_.keys
node_.values = [ndashkm] + node_.values
parentNode = node_.parent
for i, item in enumerate(p.values):
if item == value_:
parentNode.values[i] = ndashkm
break
else:
if not node_.check_leaf:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [value_]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndashk0
break
else:
ndashp0 = ndash.keys.pop(0)
ndashk0 = ndash.values.pop(0)
node_.keys = node_.keys + [ndashp0]
node_.values = node_.values + [ndashk0]
parentNode = node_.parent
for i, item in enumerate(parentNode.values):
if item == value_:
parentNode.values[i] = ndash.values[0]
break
if not ndash.check_leaf:
for j in ndash.keys:
j.parent = ndash
if not node_.check_leaf:
for j in node_.keys:
j.parent = node_
if not parentNode.check_leaf:
for j in parentNode.keys:
j.parent = parentNode
# 输出B+树
def printTree(tree):
lst = [tree.root]
level = [0]
leaf = None
flag = 0
lev_leaf = 0
node1 = Node(str(level[0]) + str(tree.root.values))
while (len(lst) != 0):
x = lst.pop(0)
lev = level.pop(0)
if (x.check_leaf == False):
for i, item in enumerate(x.keys):
print(item.values)
else:
for i, item in enumerate(x.keys):
print(item.values)
if (flag == 0):
lev_leaf = lev
leaf = x
flag = 1
record_len = 3
bplustree = BplusTree(record_len)
bplustree.insert('5', '33')
bplustree.insert('15', '21')
bplustree.insert('25', '31')
bplustree.insert('35', '41')
bplustree.insert('45', '10')
printTree(bplustree)
if(bplustree.find('5', '34')):
print("Found")
else:
print("Not found")Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Outils d'IA chauds
Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes
AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.
Undress AI Tool
Images de déshabillage gratuites
Clothoff.io
Dissolvant de vêtements AI
AI Hentai Generator
Générez AI Hentai gratuitement.
Article chaud
Outils chauds
Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit
SublimeText3 version chinoise
Version chinoise, très simple à utiliser
Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP
Dreamweaver CS6
Outils de développement Web visuel
SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
Comment modifier une table dans MySQL en utilisant l'instruction ALTER TABLE?
Mar 19, 2025 pm 03:51 PM
L'article discute de l'utilisation de l'instruction ALTER TABLE de MySQL pour modifier les tables, notamment en ajoutant / abandon les colonnes, en renommant des tables / colonnes et en modifiant les types de données de colonne.
Comment configurer le cryptage SSL / TLS pour les connexions MySQL?
Mar 18, 2025 pm 12:01 PM
L'article discute de la configuration du cryptage SSL / TLS pour MySQL, y compris la génération et la vérification de certificat. Le problème principal est d'utiliser les implications de sécurité des certificats auto-signés. [Compte de caractère: 159]
Quels sont les outils de GUI MySQL populaires (par exemple, MySQL Workbench, PhpMyAdmin)?
Mar 21, 2025 pm 06:28 PM
L'article traite des outils de GUI MySQL populaires comme MySQL Workbench et PhpMyAdmin, en comparant leurs fonctionnalités et leur pertinence pour les débutants et les utilisateurs avancés. [159 caractères]
Comment gérez-vous les grands ensembles de données dans MySQL?
Mar 21, 2025 pm 12:15 PM
L'article traite des stratégies pour gérer de grands ensembles de données dans MySQL, y compris le partitionnement, la rupture, l'indexation et l'optimisation des requêtes.
Expliquez les capacités de recherche en texte intégral InNODB.
Apr 02, 2025 pm 06:09 PM
Les capacités de recherche en texte intégral d'InNODB sont très puissantes, ce qui peut considérablement améliorer l'efficacité de la requête de la base de données et la capacité de traiter de grandes quantités de données de texte. 1) INNODB implémente la recherche de texte intégral via l'indexation inversée, prenant en charge les requêtes de recherche de base et avancées. 2) Utilisez la correspondance et contre les mots clés pour rechercher, prendre en charge le mode booléen et la recherche de phrases. 3) Les méthodes d'optimisation incluent l'utilisation de la technologie de segmentation des mots, la reconstruction périodique des index et l'ajustement de la taille du cache pour améliorer les performances et la précision.
Comment déposez-vous une table dans MySQL à l'aide de l'instruction TABLE DROP?
Mar 19, 2025 pm 03:52 PM
L'article discute de la suppression des tables dans MySQL en utilisant l'instruction TABLE DROP, mettant l'accent sur les précautions et les risques. Il souligne que l'action est irréversible sans sauvegardes, détaillant les méthodes de récupération et les risques potentiels de l'environnement de production.
Comment représentez-vous des relations en utilisant des clés étrangères?
Mar 19, 2025 pm 03:48 PM
L'article discute de l'utilisation de clés étrangères pour représenter les relations dans les bases de données, en se concentrant sur les meilleures pratiques, l'intégrité des données et les pièges communs à éviter.
Comment créez-vous des index sur les colonnes JSON?
Mar 21, 2025 pm 12:13 PM
L'article discute de la création d'index sur les colonnes JSON dans diverses bases de données comme PostgreSQL, MySQL et MongoDB pour améliorer les performances de la requête. Il explique la syntaxe et les avantages de l'indexation des chemins JSON spécifiques et répertorie les systèmes de base de données pris en charge.
